Grandeurs globales : flux magnétique
Pour calculer des forces (contre-)électromotrices (f.é.m), déterminer les grandeurs utiles lors d’un couplage avec les équations de circuits électrique, ou tout simplement identifier des inductances équivalentes, nous devrons calculer le flux magnétique traversant nos conducteurs (généralement des enroulements).
Par définition, le flux traversant une surface donnée $S$ est : $$\varphi = \iint_S {\bf b}\cdot{\bf d S}$$
On peut facilement le calculer en utilisant le potentiel vecteur. En effet, en utilisant le théorème de Stokes : $$\varphi = \iint_S ({\bf rot\,a})\cdot{\bf d S} = \oint\limits_{C =\partial S} {\bf a}\cdot{\bf d l}$$
Dans certains cas, cette formule est suffisante. Mais lorsque nous aurons des conducteurs avec des sections ne pouvant plus être considérées comme négligeables, il nous faut déterminer le « flux moyen » le traversant.
Prenons l’exemple simple d’une spire circulaire tel que schématisé ci-dessous :
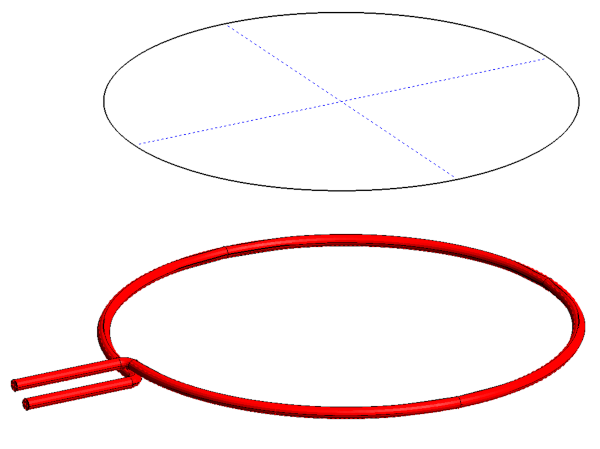
Exemple simple d'une spire (en haut : circuit filiforme, en bas : géométrie réelle).
Si la section du conducteur $S_c$ est très faible, on peut considérer la spire comme un circuit filiforme (représenté en haut de la figure) et appliquer les formules ci-dessous pour calculer le flux à travers la surface en pointillés bleus.
Mais pour une géométrie plus réaliste telle que la vraie spire dessinée en rouge, on doit déterminer le flux moyen la traversant. Un moyen simple d’y parvenir est d’utiliser la valeur moyenne du potentiel vecteur ${\bf a}$ sur une section de conducteur. Soit :
$$\varphi = \int_C \left(\frac{1}{S_c} \iint_{S_c} {\bf a}~\text{d} S\right)\cdot{\bf dl} $$ où $C$ est la longueur centrale de la spire.
On peut ainsi se ramener à l’intégrale volumique sur la spire complète (volume $V_s$) : $$\varphi = \frac{1}{S_c} \iiint_{V_s} {\bf a}\cdot{\bf u}~\text{d} V$$
${\bf u}$ étant un vecteur unitaire dirigé dans le sens du courant (orthogonal à $S_c$).
Pour un conducteur à section constante et portant un courant stationnaire $I$ :
$${\bf u} = \frac{\bf j}{|\!|{\bf j}|\!|} = \frac{S_c}{I}\,{\bf j}$$
Ainsi :
$$\boxed{\varphi = \frac{1}{I} \iiint_{V_s} {\bf a}\cdot{\bf j} ~\text{d} V}$$
L’expression ci-dessus est particulièrement intéressante car elle nous permet de retrouver facilement la relation entre l’énergie magnétique et le flux ou l’inductance. En effet, on a directement : $$\varphi = \frac{2}{I}\,W_{mag}$$ Soit : $$\boxed{W_{mag} = \frac{1}{2}\,\varphi\,I}$$ En linéaire, puisque par définition, l’inductance $L$ du conducteur est : $$ L = \frac{\varphi}{I}$$ On a également l’expression bien connue (valable uniquement en linéaire): $$\boxed{W_{mag} = \frac{1}{2}\,L\,I^2}$$