Boîtes Infinies

Une dernière remarque avant de clôturer ce cours : vous avez peut-être remarqué dans certains des exemples précédents une bande d’éléments placée le long des frontières. Celle-ci est une technique particulière permettant de prendre parfaitement en compte les frontières « lointaines ». Elle permet ainsi de réduire le domaine d’étude du problème. On l’appelle souvent boîte infinie.

Principe avec une boîte sphérique

Il n’est pas rare que le dispositif étudié soit entouré d’une zone d’air dans laquelle les champs électriques ou magnétiques s’épanouissent, obligeant le modélisateur à éloigner les frontières pour ne pas dénaturer la forme des champs calculés. Une autre approche consiste à définir un domaine d’air réduit entouré par une coquille sphérique (spherical shell).

Le domaine d’étude $\Omega$ est alors divisé en deux parties :

  • le dispositif et l’air environnant : $\Omega_i$ ;
  • la boîte sphérique, de rayon intérieur $R_i$ et extérieur $R_e$, correspondant à cette coquille : $\Omega_\infty$, de bord extérieur $\Gamma_\infty$

Un exemple est donné sur la figure ci-dessous.

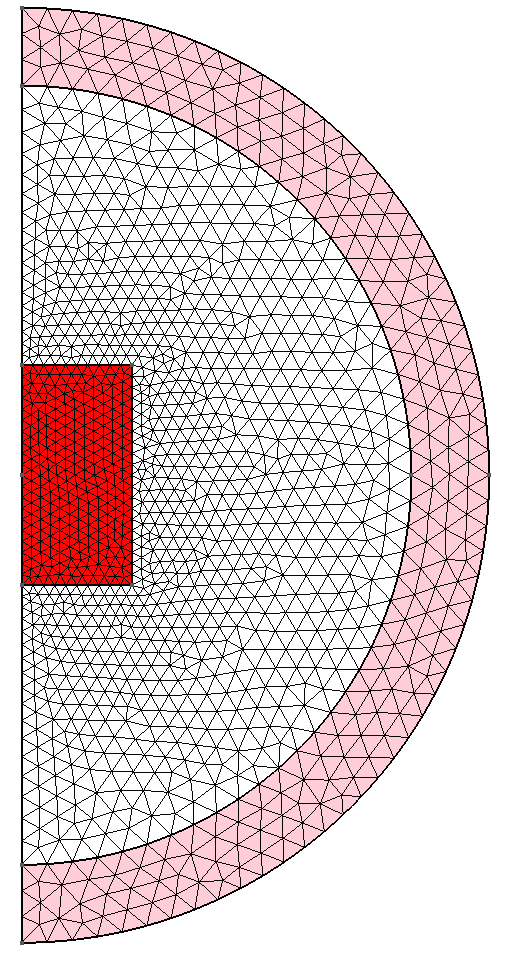
Exemple d'une boîte infinie sphérique (en rose) entourant un aimant permanent cylindrique (en rouge) modélisé en 2D axisymétrique

L’idée générale est d’appliquer une transformation bijective qui fait correspondre le reste de l’espace ($\mathbb{R}^3\backslash\Omega_i$) à la région $\Omega_\infty$ construite à partir de la relation :

$$\|{\bf x}\| = R_i \frac{R_e-R_i}{R_e-\|{\bf X}\|}$$

où ${\bf X}$ représente le vecteur position dans la boîte $\Omega_\infty$.

La transformation $\boldsymbol{\mathcal{F}} : \mathbb{R}^3\backslash\Omega_i \to\Omega_{\infty}$ est ainsi donnée par :

$$ {\bf X} = \boldsymbol{\mathcal{F}}({\bf x}) = \frac{\|{\bf X}\|}{\|{\bf x}\|}\,{\bf x} =\left[\frac{R_e}{\|{\bf x}\|} - \frac{R_i (R_e-R_i)}{\|{\bf x}\|^2} \right]\,{\bf x}$$

Ainsi, une condition du type ${\bf b}\xrightarrow[\|{\bf x}\|\to \infty]{}{\bf 0}$ peut se ramener à imposer une condition de Dirichlet homogène sur $\Gamma_\infty$, et en s’appuyant sur la matrice jacobienne ${\bf J_{\mathcal{F}}}$ de la transformation $\boldsymbol{\mathcal{F}}$, on a la relation (dans le cas de notre exemple, avec une formulation en potentiel vecteur) :

$$\displaystyle\iiint_{\mathbb{R}^3} \nu\,{\bf rot\,a}\cdot{\bf rot a'}~\text{d}\,\Omega = \iiint_{\Omega_i} \nu\,{\bf rot\,a}\cdot{\bf rot a'}~\text{d}\,\Omega + \iiint_{\Omega_{\infty}} \nu\,{\bf J_{\mathcal{F}}^{-1}}\,{\bf rot\,a} \cdot {\bf J_{\mathcal{F}}^{-1}}\,{\bf rot\,a'}~|\det \mathbf{J}_{\mathcal{F}}|~\text{d}\,\Omega$$

Pour résumer : résoudre avec une boîte infinie est équivalent à résoudre sur $\mathbb{R}^3$ entier.

Dans GetDP, cela se définit simplement en choisissant le Jacobien adéquat dans la partie correspondante (sans oublier la condition de Dirichlet sur le bord).
Par exemple dans le cas présent on utilisera pour le domaine $\Omega_\infty$ : un VolAxiSphShell pour Volumic Axisymetric Spherical Shell :

Jacobian{
  { Name Jvol;
    Case {
      { Region boite_inf ; Jacobian VolAxiSphShell{Ri,Re} ;} // boîte infinie
      { Region All ; Jacobian VolAxi ; }                  // reste du domaine
    }
  }
}
Astuce

En plus de boîtes sphériques, on peut aussi utiliser des procédés analogues pour définir des boîtes infinies rectangulaires ou cylindriques.

Exemple de résultat

Voici la carte de la norme de l’induction et les lignes de champs associées (isovaleurs de $r\,a_{\theta}$) sur notre exemple d’un aimant permanent cylindrique (Br = 1,2 T, formulation en potentiel vecteur à l’ordre 2) :

Sans boîte infinie Avec boîte infinie
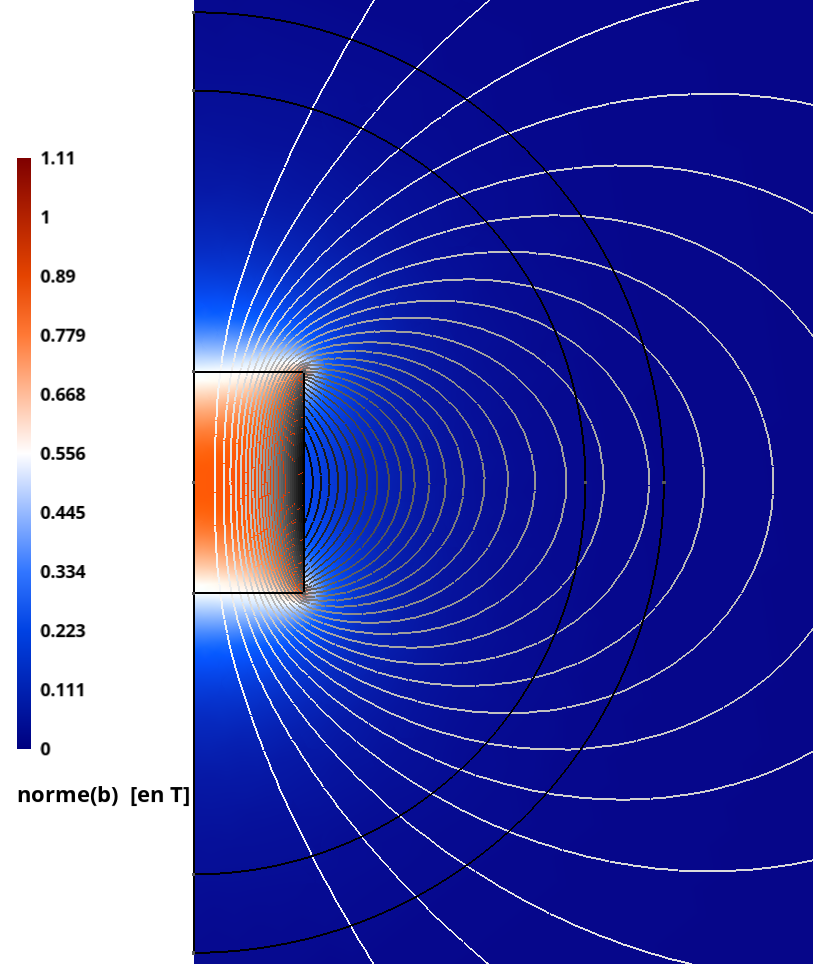
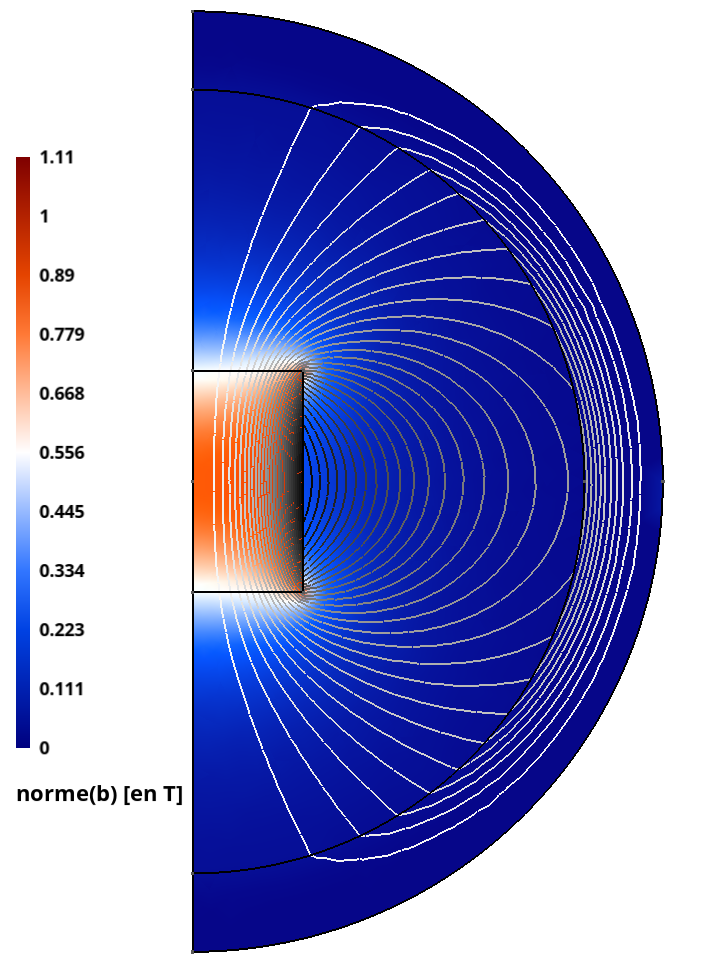
Norme de b et lignes de champ d’un aimant permanent cylindrique Norme de b et lignes de champ d’un aimant permanent cylindrique Norme de b et lignes de champ d’un aimant permanent cylindrique Norme de b et lignes de champ d’un aimant permanent cylindrique

Pour le cas sans boîte infinie, on a choisi une taille de domaine très grande devant le rayon de l’aimant. On remarquera que les résultats sont strictement identiques dans $\Omega_i$, preuve de l’efficacité de la méthode.