Résolution par des Méthodes Numériques

Nous allons voir le principe de cette méthode numérique en nous intéressant aux premières itérations :

On se fixe un pas de calcul \(h\), de préférence petit.

Puisqu'on a une condition initiale , on connaît \(x_0\) et \(y(x_0)\), que l'on note \(y_0\).

On calcule alors \(y_1\) par application de la formule :

\(y_{1} = y_0 + h \cdot f(x_0,y_0)\)

On considère alors que \(y_1~\#~y(x_1)\), avec \(x_1 = x_0 + h\), on peut donc calculer \(y_2\).

\(y_{2} = y_1 + h \cdot f(x_1,y_1)\) 

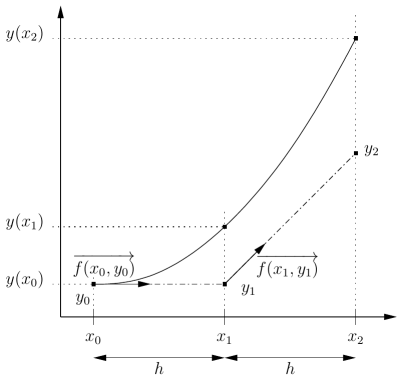
Et ainsi de suite jusqu'à la fin du domaine d'étude. Graphiquement, le procédé est représenté sur la figure ci-dessous.

Soit le problème suivant défini sur \([a,b]\) :

\(\left\{ \begin{array}{l} y'=f(x,y) \\ y(a) = y_a \end{array} \right.\)

L'algorithme de résolution correspondant est :

En sortie de l'algorithme on obtient le vecteur \((y_0,\dots,y_n)\) correspondant au \(n+1\) valeurs de la solution approchée \(\tilde{y}\) associées à \((x_0,\dots,x_n)\).