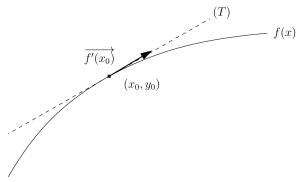
Notions de tangente et d'approximation à l'ordre 1
Soit la courbe représentative d'une fonction \(f(x)\) au point \((x_0,y_0)\), et \((T)\) sa tangente au même point (cf figure).
Dans le plan, l'équation de \((T)\) est :
\(y = f'(x_0)~(x-x_0) + y_0\).
Ce qui est la même chose que :
\(t(x) = f'(x_0)~(x-x_0) + f(x_0)\)
Donc, dans la méthode d'Euler, on considère que, lorsqu'on est assez proche de \(x_0\), on a :
\(f(x)\approx t(x) = f'(x_0)~(x-x_0) + f(x_0)\).
(On reconnaît le développement de Taylor à l'ordre 1 de \(f\)).
En posant \(h=(x-x_0)\), on obtient (pour \(h\) petit) :
\(f(x) = f(x_0) + h~f'(x_0)\).
Ce qu'on appelle « approximation du premier ordre » de \(f\).