Électrocinétique

Dans le cas de l’électrocinétique (en anglais electrokinetics ou current flow), nous nous intéresserons au calcul de la distribution de la densité volumique statique de courrant électrique ${\bf j}$ dans des conducteurs.

Les relations intervenant en électrocinétique sont :

  • Les équations de Maxwell en statique suivantes :

    $$\left\{\begin{aligned}\text{div}\,{\bf j} &= 0 \\ {\bf rot}\,{\bf e} &= {\bf 0} \end{aligned}\right.$$

  • La loi de comportement dans les milieux conducteurs électriques :

    $${\bf j} = \sigma\,{\bf e}$$

  • Pour les conditions au limites, c’est-à-dire aux frontières du domaine d’étude $\Omega_c$, nous aurons :

    • soit, d’après la condition sur la composante tangentielle de ${\bf e}$ sur les faces d’entrée ou sortie du courant $(\Gamma_d)$ : $$\left.{\bf n}\wedge{\bf e}\right|_{\Gamma_d} = {\bf 0}$$
    • soit, d’après la condition sur la composante normale de ${\bf j}$ sur les autres bords du conducteurs $(\Gamma_n)$ : $$\left.{\bf n}\cdot{\bf j}\right|_{\Gamma_n} = 0$$

Formulation forte

Comme en électrostatique, nous pouvons définir le potentiel scalaire électrique $v$ tel que : ${{\bf e} = -{\bf grad}\,v}$.

En réinjectant cette relation couplée à la loi de comportement dans la loi des nœuds locale, on obtient :

$$ \text{div}\left(\sigma\,{\bf grad}\,v \right) = 0$$

Sur les faces d’entrée et de sortie du courant (${\Gamma_d = \Gamma_{di}\cup\Gamma_{dj}}$), deux cas seront possibles :

  1. Soit une condition de potentiel imposé par une condition de Dirichlet sur $\Gamma_{di}$ de type : $$v|_{\Gamma_{di}} = v_i$$
  2. Soit une condition de Neumann non-homogène imposant la densité de courant normale à la surface $\Gamma_{dj}$ : $$\left.\frac{\partial\,v}{\partial {\bf n}}\right|_{\Gamma_{dj}} = {\bf grad}\,v\cdot {\bf n}\big|_{\Gamma_{dj}} = \pm \frac{j_{n_j}}{\sigma}$$

Sur les autres bords du domaine $(\Gamma_n)$, nous aurons des conditions de Neumann homogènes : ${{\bf grad}\,v\cdot {\bf n}\big|_{\Gamma_{n}} = 0}$

Finalement, la forme complète de la formulation forte à résoudre est donc :

$$\left\{\begin{aligned}\text{div}\left(\sigma\,{\bf grad}\,v\right) &= 0~ , &\text{dans}~ \Omega_c \\ \left.v\right|_{\Gamma_{di}} &= v_i~ , &\text{sur}~ \Gamma_{di} \\ \left.{\bf grad}\, v \cdot {\bf n}\right|_{\Gamma_{dj}} &= \pm \frac{j_{n_j}}{\sigma}~ , &\text{sur}~ \Gamma_{d_j} \\ \left.{\bf grad}\, v \cdot {\bf n}\right|_{\Gamma_n} &= 0~ , &\text{sur}~ \Gamma_n \end{aligned}\right.$$

Formulation faible

La formulation faible correspondant à la forme forte ci-dessus est obtenue rapidement par analogie avec l’électrostatique :

Trouver $v \in \text{H}_{0}({\bf grad},\Omega) = \{ u \in \text{H}({\bf grad},\Omega) : u|_{\Gamma_{di}} = v_i \}$, tel que :

$$\forall v' \in \text{H}_{0}({\bf grad},\Omega),~~ \left(\sigma\,{\bf grad}\,v,{\bf grad}\,v'\right)_{\Omega} + \left< j_{n_j},v' \right>_{\Gamma_{dj}} = 0$$

Exemples et applications

Résistance de sole de four électrique

On considère une résistance de sole de four électrique telle que représentée ci-dessous : Résistance de sole Résistance de sole

On désire calculer la distribution de la densité de courant à l’intérieur lorsqu’on applique une tension de 230 V à ses bornes, afin d’en déduire sa résistance via les pertes Joule associées.

L’implantation dans GetDP ressemble beaucoup au cas précédent :

Constraint {	
  {Name Dirichlet ;
    Case {      
      {Region Sentree ; Type Assign ; Value Veff ;}
      {Region Ssortie ; Type Assign ; Value 0. ;}
    }
  }
}

FunctionSpace {
  { Name Hgrad_v ; Type Form0 ; 
    BasisFunction { 
      { Name sn ; NameOfCoef vn ; Function BF_Node ; 
		Support Region[{Domaine}]  ; Entity NodesOf[All] ; }
    } 
    Constraint {
      { NameOfCoef vn  ; EntityType NodesOf ; NameOfConstraint Dirichlet ; }
    }
  }
}


Formulation {
  { Name Electrocinetique ; Type FemEquation ;
    Quantity {
      { Name v  ; Type Local  ; NameOfSpace Hgrad_v ; }
    } 
    Equation {
      Galerkin { [ Sigma[]*Dof{Grad v}  , {Grad v} ] ;
		In Domaine ; Jacobian Jvol ; Integration Integ ; }
     }
  }
}

Après calcul, on obtient pour la répartition du potentiel scalaire électrique : v dans résistance de sole v dans résistance de sole

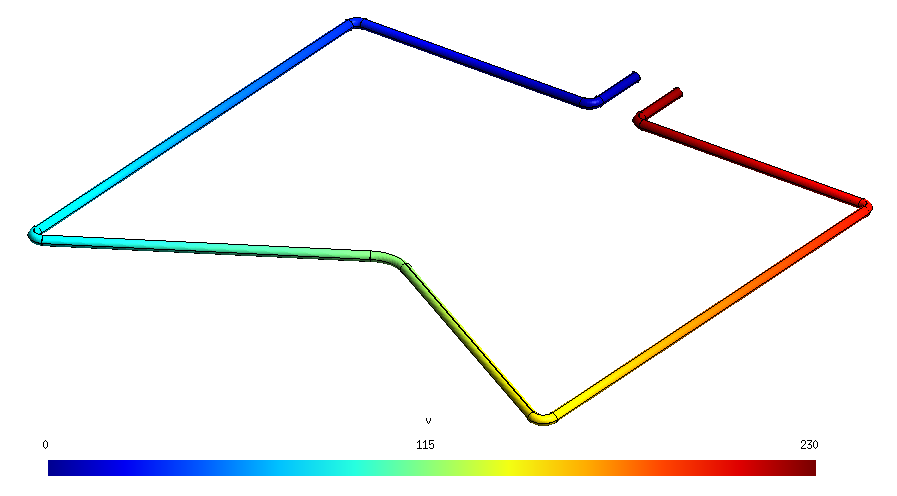
Vous pouvez télécharger les fichiers complets en cliquant ici .

Pour la petite histoire, voici une photo de celle de mon four perso après démontage pour changement suite à un défaut d’isolement : Ma resistance de sole perso Ma resistance de sole perso

Résistance de charge

  1. Traiter le problème analogue sur une forme correspondant aux résistances de charge utilisées sur nos bancs expérimentaux : “Résistances de charges pour manip” “Résistances de charges pour manip”

  2. En dimensionner une permettant de dissiper 5 kW sous 48 V continus.
    On pourra utiliser comme conducteur du Constantan, par exemple du 45Ni-55Cu de résistivité électrique : $\rho = 14,9\cdot 10^{-7}~\Omega\cdot\text{m}$

Astuce

Pour la géométrie, on pensera à utiliser une extrusion combinant à la fois une translation selon le vecteur $(v_{t_x},v_{t_y},v_{t_z})$ et une rotation d’un angle $\alpha$ autour de l’axe de vecteur directeur $(v_{a_x},v_{a_y},v_{a_z})$ et passant par le point $(x_a,y_a,z_a)$. Dans Gmsh, cela se définit de façon la plus simple :
Extrude{ {vtx,vty,vtz}, {vax,vay,vaz}, {xa,ya,za}, alpha } { Surface{numero}; }
ou de façon un peu plus élaborée (si on veut structurer le maillage) :
sortie[] = Extrude{ {vtx,vty,vtz}, {vax,vay,vaz}, {xa,ya,za}, alpha } { Surface{numero}; Layers{Ncouches}; Recombine; };

Busbar avec potentiel flottant

Tout comme dans le cas électrostatique de la section précédente, il est possible de définir, dans l’espace fonctionnel d’approximation $W^0$ , des grandeurs globales associées à notre inconnue $v$. Dans le cas présent, elles correspondront aux potentiels globaux $V_i$ imposés sur certaines faces du bords du domaine, ou aux courants $I_j$ traversant certaines autres.

  1. En utilisant (ou pas) ces grandeurs globales, calculer la distribution de courant à l’intérieur du busbar en cuivre représenté ci-dessous lorsque qu’un courant de 2000 A arrive par le haut et se sépare en 2 fois 1000 A qui sortent par le bas. “Busbar” “Busbar” Pour éviter de perdre trop de temps, je vous fournis la géométrie (libre à vous de l’utiliser ou non) : Cliquer ici pour la télécharger .

  2. Proposer des améliorations possibles du design d’un tel busbar (en terme de quantité de matière, masse, volume, pertes…).