Deuxième tuto : un aimant
But du tuto : apprendre à définir un aimant et connaître les différentes façons de modéliser une frontière lointaine.
Notions abordées :
- définition d'un aimant permanent ;
- techniques particulières pour la frontière du domaine :
- transformation de Kelvin
- « frontière ouverte » / boîte infinie.
Nous poursuivons nos tutos d'apprentissage avec un exemple tout aussi simple d'un point de vue géométrique : un aimant permanent cylindrique dans l'air. On prendra des dimensions similaires à celles de l'intérieur de la bobine précédente : rayon \(R\), hauteur \(b\). L'induction rémanente de l'aimant, polarisé axialement, est \(B_r = 1,2\,\text{T}\), et sa perméabilté relative est \(\mu_r = 1,05\).
Méthode « classique »
Le début du programme sera donc identique au précédent. Dans un fichier aimant.m, on rentre :
- MATLAB :
% Fichier aimant.m simulant l'aimant du second tuto avec FEMM
close all
clear
clc
addpath('C:\femm42\mfiles')
% Donnes probleme
R = 10; % mm
b = 20; % mm
Rdom = 10*sqrt(R^2+(b/2)^2); % on prend un domaine tres large
openfemm()
newdocument(0) % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique
% Geometrie
mi_drawrectangle(0,b/2,R,-b/2); % aimant
% domaine :
mi_addnode(0,-Rdom);
mi_addnode(0,Rdom);
mi_addsegment(0,-Rdom,0,-b/2);
mi_addsegment(0,b/2,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5);
mi_zoomnatural;
- Python :
# Fichier aimant.py simulant l'aimant du second tuto avec FEMM
import numpy as np
import femm
# Donnes probleme
R = 10 # mm
b = 20 # mm
Rdom = 10*np.sqrt(R**2+(b/2)**2) # on prend un domaine tres large
femm.openfemm()
femm.newdocument(0) # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique
# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2) # aimant
# domaine :
femm.mi_addnode(0,-Rdom)
femm.mi_addnode(0,Rdom)
femm.mi_addsegment(0,-Rdom,0,-b/2)
femm.mi_addsegment(0,b/2,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5)
femm.mi_zoomnatural()
Dans un premier temps, nous choisissons un domaine très large : 10 fois la diagonale du bloc "aimant", pour être certain de ne pas dénaturer le problème.
Il nous faut maintenant définir les matériaux. Dans FEMM, un aimant permanent est caractérisé par :
- sa perméabilité relative \(\mu_r\),
- son champ coercitif \(H_c\) en \(\text{A}\cdot\text{m}^{-1}\),
- la direction de son aimantation (angle par rapport à l'axe des abscisses en degrés).
La courbe \(B(H)\) d'un aimant peut se représenter de la façon suivante :
FEMM utilise la droite passant par \((-H_c, 0)\) et \((0,B_r)\). On voit alors directement que : \[H_c = \frac{B_r}{\mu_0\,\mu_r}\]
Finalement, on peut créer nos matériaux et les affecter aux régions correspondantes. Et on ajoute la condition aux limites de Dirichlet sur le bord :
- MATLAB :
Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);
mi_addmaterial('Air',1,1);
mi_addmaterial('Aimant',mur,mur,Hc);
mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0); % automesh, 90° pour aimantion, groupe 2
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',1,0,0,0,1,0); % automesh, groupe 1
mi_clearselected;
mi_addboundprop('a=0',0,0,0,0);
mi_selectarcsegment(Rdom,0);
mi_setarcsegmentprop(5,'a=0',0,1);
mi_clearselected;
mi_saveas('aimant.FEM');
- Python :
Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)
femm.mi_addmaterial('Air',1,1)
femm.mi_addmaterial('Aimant',mur,mur,Hc)
femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0) # automesh, 90° pour aimantion, groupe 2
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0) # automesh, groupe 1
femm.mi_clearselected()
femm.mi_addboundprop('a=0',0,0,0,0)
femm.mi_selectarcsegment(Rdom,0)
femm.mi_setarcsegmentprop(5,'a=0',0,1)
femm.mi_clearselected()
femm.mi_saveas('aimant.FEM')
Nous avons volontairement laissé le choix de discrétisation automatique (automesh) pour voir.
On peut alors résoudre, visualiser les résultats et calculer l'énergie magnétique due à l'aimant :
- MATLAB :
mi_analyze();
mi_loadsolution;
mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;
- Python :
femm.mi_analyze()
femm.mi_loadsolution()
femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()
➤ Observez l'inversion de la direction de \({\bf h}\) dans l'aimant avec le tracé de vecteurs (densifiez la grille de tracé si besoin en cliquant sur l'icône "grid size" ou avec un mi_setgrid(R/10,'cart') par exemple), ainsi que l'ordre de grandeur de l'énergie par rapport à celle de la bobine précédente.
Remarque : Pour le calcul de l'énergie (ou de la coénergie) dans l'aimant, je vous renvoie à la page dédiée sur le Wiki de FEMM qui l'explique très bien. On retiendra que, pour un aimant, on peut utiliser : \[ w_{\text{mag}} = \frac{1}{2}\,\mu\, |\!|{\bf h}|\!|^2, ~ ~ \text{et} ~ ~ \widetilde{w}_{\text{mag}} = \frac{1}{2\,\mu} |\!|{\bf b}|\!|^2 \]
On peut constater l'intérêt de prendre un domaine assez large en comparant les valeurs d'énergie calculées pour différents rayons de domaine (Rdom) :
| Rdom | Wmag (en J) | écart |
|---|---|---|
| \(20\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,125 | référence |
| \(10\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,115 | -0,9 % |
| \(5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,118 | -0,6 % |
| \(2\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,257 | 11,7 % |
| \(1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,467 | 30,4 % |
En général, 5 fois la longueur caractéristique du dispositif est suffisante.
Sur notre exemple, on obtient la distribution de champ suivante :
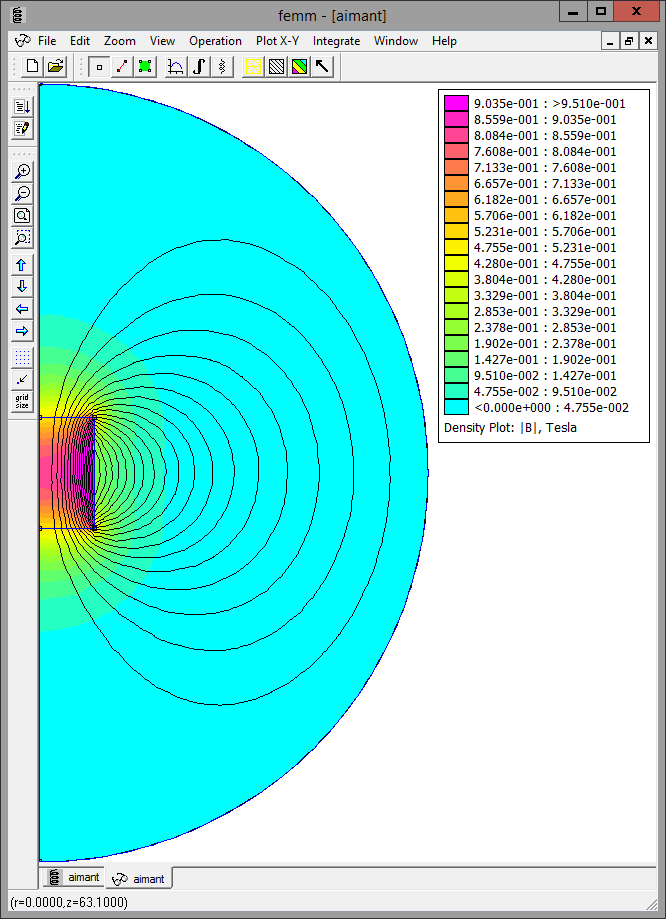
Cependant, pour de gros problèmes basés sur des géométries complexes nécessitant de nombreux éléments, il peut être intéressant de réduire le domaine d'étude afin de réduire la taille du système à résoudre (et donc le temps de calcul). FEMM dispose de deux techniques le permettant : nous allons donc les tester.
Transformation de Kelvin
Reprenons le problème précédent en le modifiant légèrement. Le rayon du domaine Rdom est réduit et nous ajoutons au dessus de celui-ci une petite sphère de rayon Rext.
- MATLAB :
% Fichier aimant_TK.m simulant l'aimant du second tuto avec FEMM
% Version avec transfo de Kelvin (region exterieure)
close all
clear
clc
addpath('C:\femm42\mfiles')
% Donnes probleme
R = 10; % mm
b = 20; % mm
Rdom = 2*sqrt(R^2+(b/2)^2); % on prend un domaine reduit
Rext = Rdom/4; % rayon region exterieure
openfemm()
newdocument(0) % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique
% Geometrie
mi_drawrectangle(0,b/2,R,-b/2); % aimant
% domaine :
mi_addnode(0,-Rdom);
mi_addnode(0,Rdom);
mi_addsegment(0,-Rdom,0,-b/2);
mi_addsegment(0,b/2,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5);
% region exterireure :
mi_addnode(0,Rdom+2*Rext);
mi_addsegment(0,Rdom,0,Rdom+2*Rext);
mi_addarc(0,Rdom,0,Rdom+2*Rext,180,5);
mi_zoomnatural;
- Python :
# Fichier aimant_TK.py simulant l'aimant du second tuto avec FEMM
# Version avec transfo de Kelvin (region exterieure)
import numpy as np
import femm
# Donnes probleme
R = 10 # mm
b = 20 # mm
Rdom = 2*np.sqrt(R**2+(b/2)**2) # on prend un domaine reduit
Rext = Rdom/4 # rayon region exterieure
femm.openfemm()
femm.newdocument(0) # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique
# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2) # aimant
# domaine :
femm.mi_addnode(0,-Rdom)
femm.mi_addnode(0,Rdom)
femm.mi_addsegment(0,-Rdom,0,-b/2)
femm.mi_addsegment(0,b/2,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5)
# region exterireure :
femm.mi_addnode(0,Rdom+2*Rext)
femm.mi_addsegment(0,Rdom,0,Rdom+2*Rext)
femm.mi_addarc(0,Rdom,0,Rdom+2*Rext,180,5)
femm.mi_zoomnatural()
Nous créons ensuite nos matériaux comme précédemment, mais en plus nous ajoutons ce que FEMM appelle une « région extérieure » associée à notre problème et que nous lions à notre petite sphère (définie comme de l'air environnant).
- MATLAB :
Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);
mi_addmaterial('Air',1,1);
mi_addmaterial('Aimant',mur,mur,Hc);
mi_defineouterspace(Rdom+Rext/2,Rext,Rdom); % region exterieure
mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0); % automesh, 90° pour aimantion, groupe 2
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',1,0,0,0,1,0); % automesh, groupe 1
mi_clearselected;
mi_addblocklabel(Rext,Rdom+Rext);
mi_selectlabel(Rext/2,Rdom+Rext);
mi_setblockprop('Air',1,0,0,0,1,0); % automesh, groupe 1
mi_attachouterspace; % dans region exterieure
mi_clearselected;
- Python :
Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)
femm.mi_addmaterial('Air',1,1)
femm.mi_addmaterial('Aimant',mur,mur,Hc)
femm.mi_defineouterspace(Rdom+Rext/2,Rext,Rdom) # region exterieure
femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0) # automesh, 90° pour aimantion, groupe 2
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0) # automesh, groupe 1
femm.mi_clearselected()
femm.mi_addblocklabel(Rext,Rdom+Rext)
femm.mi_selectlabel(Rext/2,Rdom+Rext)
femm.mi_setblockprop('Air',1,0,0,0,1,0) # automesh, groupe 1
femm.mi_attachouterspace() # dans region exterieure
femm.mi_clearselected()
Il ne reste plus qu'à créer une condition de périodicité liant le bord du domaine à celui de la région extérieure.
- MATLAB :
% condition de periodicite :
mi_addboundprop('Periodique',0,0,0,0,0,0,0,0,4);
mi_selectarcsegment(Rdom,0); % bord domaine
mi_selectarcsegment(Rext,Rdom+Rext); % bord region exterieure
mi_setarcsegmentprop(5,'Periodique',0,1);
mi_clearselected;
mi_saveas('aimant.FEM');
- Python :
# condition de periodicite :
femm.mi_addboundprop('Periodique',0,0,0,0,0,0,0,0,4)
femm.mi_selectarcsegment(Rdom,0) # bord domaine
femm.mi_selectarcsegment(Rext,Rdom+Rext) # bord region exterieure
femm.mi_setarcsegmentprop(5,'Periodique',0,1)
femm.mi_clearselected()
femm.mi_saveas('aimant.FEM')
Comment ça marche ?
Dans la région extérieure, la formulation a été modifiée par un changement de variable \(r \mapsto R\) tel que \(\frac{1}{R} \to 0\) lorsqu'on s'approche du centre de la petite sphère. Ainsi, le centre de la région est équivalent à l'\(\infty\). Le lien avec le domaine d'étude est assuré par une condition de périodicité égalisant les valeurs de \(a_\theta\) sur leurs frontières respectives. Pour simplifier : tout se passe comme si on avait « replié » la partie de l'espace située en dehors du domaine d'étude dans la petite sphère du dessus.
On peut ensuite résoudre notre problème et calculer l'énergie :
- MATLAB :
mi_analyze();
mi_loadsolution;
mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;
- Python :
femm.mi_analyze()
femm.mi_loadsolution()
femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()
Calculons l'énergie pour les deux dernières valeurs de Rdom du paragraphe précédent :
| Rdom (avec TK) | Wmag (en J) | écart avec la référence |
|---|---|---|
| \(2\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,121 | -0,4 % |
| \(1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,144 | 1,7 % |
Un exemple de résultats obtenus est montré sur la figure ci-dessous représentant l'induction :
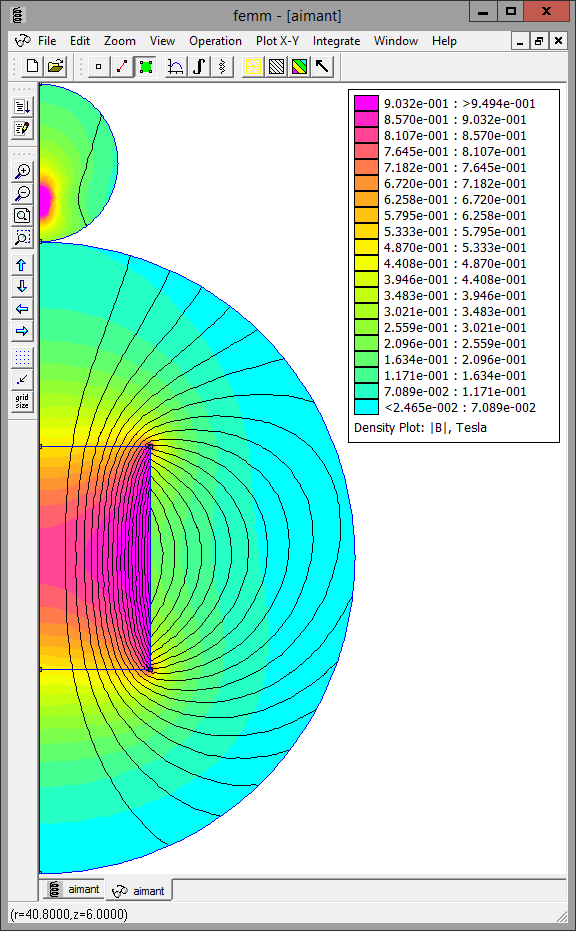
On voit clairement l'efficacité de la méthode.
Frontière ouverte (~ boîte infinie)
Une autre technique permettant de réduire le domaine d'étude est d'utiliser une condition de « frontière ouverte ». L'idée est de se rapprocher du fonctionnement d'une boîte infinie via l'utilisation de ce que l'auteur du logiciel appelle « une condition au limite asymptotique improvisée » (Improvised Asymptotic Boundary Conditions).
Contrairement à une vraie boîte infinie où l'expression du jacobien dans les bords de la boîte est modifié pour correspondre à un domaine non borné, FEMM utilise une boîte circulaire dont le bord est constitué de plusieurs couches où les valeurs de perméabilités sont modifiées pour correspondre à différents développements asymptotiques du potentiel vecteur 2D successifs. Voir ici pour plus de détails.
Même si cette technique est moins rigoureuse, mathématiquement parlant, que la transformation de Kelvin ou une vraie boîte infinie, elle fournie de très bons résultats et est surtout très facile à implanter dans FEMM :
- pas besoin de créer le domaine,
- pas besoin de créer une condition au limite particulière,
- une seule instruction :
mi_makeABC();(les options par défaut sont, la plupart du temps, très bien choisies).
Le script pour résoudre complètement notre problème devient ainsi plus concis :
- MATLAB :
% Fichier aimant_OB.m simulant l'aimant du second tuto avec FEMM
% Version avec condition « open boundary »
close all
clear
clc
addpath('C:\femm42\mfiles')
% Donnes probleme
R = 10; % mm
b = 20; % mm
openfemm()
newdocument(0) % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique
% Geometrie
mi_drawrectangle(0,b/2,R,-b/2); % aimant
mi_makeABC(); % domaine (open boudary)
mi_zoomnatural;
% Physique
Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);
mi_addmaterial('Air',1,1);
mi_addmaterial('Aimant',mur,mur,Hc);
mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0);
mi_clearselected;
mi_addblocklabel(1.2*R,0);
mi_selectlabel(1.2*R,0);
mi_setblockprop('Air',1,0,0,0,1,0);
mi_clearselected;
mi_saveas('aimant.FEM')
mi_analyze();
mi_loadsolution;
mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;
- Python :
# Fichier aimant_OB.py simulant l'aimant du second tuto avec FEMM
# Version avec condition « open boundary »
import numpy as np
import femm
# Donnes probleme
R = 10 # mm
b = 20 # mm
femm.openfemm()
femm.newdocument(0) # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique
# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2) # aimant
femm.mi_makeABC() # domaine (open boudary)
femm.mi_zoomnatural()
# Physique
Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)
femm.mi_addmaterial('Air',1,1)
femm.mi_addmaterial('Aimant',mur,mur,Hc)
femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0)
femm.mi_clearselected()
femm.mi_addblocklabel(1.2*R,0)
femm.mi_selectlabel(1.2*R,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0)
femm.mi_clearselected()
femm.mi_saveas('aimant.FEM')
femm.mi_analyze()
femm.mi_loadsolution()
femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()
On obtient alors les résultats décrits par la figure et la table ci-dessous :
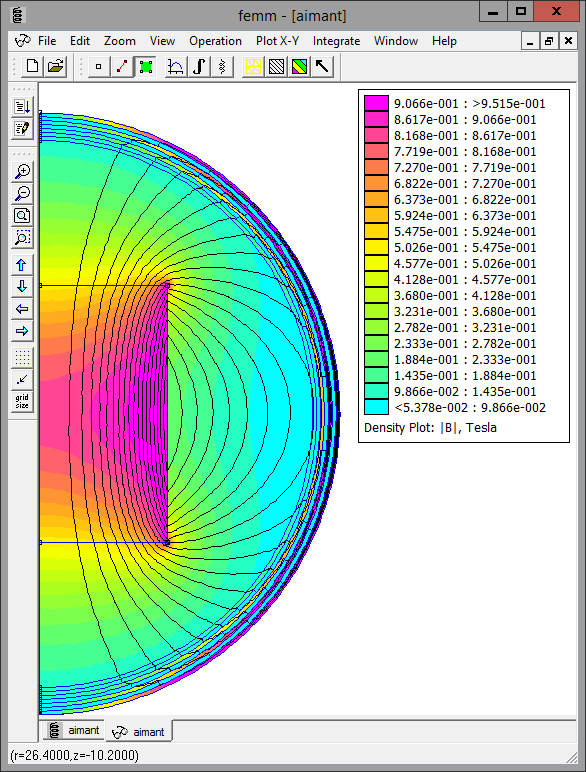
| Rdom (open boundary) | Wmag (en J) | écart avec la référence |
|---|---|---|
| \(\approx 1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}\) | 1,102 | -2,0 % |
Ce qui est tout à fait acceptable.