Premier tuto : une bobine
But du tuto : apprendre à définir un premier problème simple de magnétostatique et le résoudre.
Notions abordées :
- création de la géométrie ;
- définition de la physique et affectation ;
- maillage et résolution ;
- quelques calculs post-traitement, en particulier le flux magnétique.
On considère une bobine de fils de cuivre cylindrique, de rayon \(R\), d'épaisseur \(a\) et de hauteur \(b\), telle que représentée sur la figure ci-dessous. Elle est constituée de \(N\) spires parcourues par un courant \(I_c\).
Le but est de calculer le champ qu'elle produit, l'énergie correspondante, ainsi que son inductance propre.
Définition du problème
Pour commencer, on crée (au bon endroit) un fichier bobine.m ou bobine.py par exemple, et on y rentre le préambule « classique » :
- MATLAB :
% Fichier bobine.m simulant la bobine du premier tuto avec FEMM
close all
clear
clc
addpath('C:\femm42\mfiles')
- Python :
# Fichier bobine.py simulant la bobine du premier tuto avec FEMM
import numpy as np
import femm
On ajoute les valeurs des paramètres :
- MATLAB :
% Donnes probleme
R = 10; % mm
a = 10; % mm
b = 20; % mm
N = 100;
Ic = 5; % A
% Grandeurs annexes
Rdom = 5*sqrt((R+a)^2+(b/2)^2); % Rayon du domaine
- Python :
# Donnees du probleme
R = 10.0 # mm
a = 10.0 # mm
b = 20.0 # mm
N = 100
Ic = 5.0 # A
# Grandeurs annexes
Rdom = 5*np.sqrt((R+a)**2+(b/2)**2) # Rayon du domaine
On peut alors ouvrir FEMM :
openfemm()
ou
femm.openfemm()
Remarque : Parfois, il peut être utile de démarrer FEMM en mode "minimisé" (pendant des procédés itératifs où on effectue plusieurs calculs de suite). On peut le faire directement par :
openfemm(1)
Débutons un nouveau problème magnétique et spécifions ces propriétés :
- MATLAB :
newdocument(0) % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique
- Python :
femm.newdocument(0) # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique
Géométrie
On peut ensuite passer à la création de la géométrie. C'est un simple rectangle : on crée les quatre sommets et les quatre côtés par :
- MATLAB :
% Definition de la geometrie
%-------------------------------
% Creation des points (noeuds) :
mi_addnode(R,b/2);
mi_addnode(R+a,b/2);
mi_addnode(R+a,-b/2);
mi_addnode(R,-b/2);
% Creation des segments :
mi_addsegment(R,b/2,R+a,b/2);
mi_addsegment(R+a,b/2,R+a,-b/2);
mi_addsegment(R+a,-b/2,R,-b/2);
mi_addsegment(R,-b/2,R,b/2);
- Python :
# Definition de la geometrie
#-------------------------------
# Creation des points (noeuds) :
femm.mi_addnode(R,b/2)
femm.mi_addnode(R+a,b/2)
femm.mi_addnode(R+a,-b/2)
femm.mi_addnode(R,-b/2)
# Creation des segments :
femm.mi_addsegment(R,b/2,R+a,b/2)
femm.mi_addsegment(R+a,b/2,R+a,-b/2)
femm.mi_addsegment(R+a,-b/2,R,-b/2)
femm.mi_addsegment(R,-b/2,R,b/2)
Remarque : Ceci est la façon la plus basique de procéder, on aurait pu utiliser des fonctions plus évoluées comme
mi_drawpolyline(MATLAB uniquement),mi_drawpolygon(MATLAB uniquement) ou, encore mieux dans notre cas,mi_drawrectangle. Pour notre rectangle, on aurait donc pu faire :
mi_drawpolyline([R,b/2;R+a,b/2;R+a,-b/2;R,-b/2;R,b/2])(MATLAB)mi_drawpolygon([R,b/2;R+a,b/2;R+a,-b/2;R,-b/2])(MATLAB)mi_drawrectangle(R,b/2,R+a,-b/2)(MATLAB ou Python)Ce qui est évidemment beaucoup plus compact...
Pour le domaine d'air environnant, nous allons définir un demi-disque de rayon Rdom :
- MATLAB :
mi_drawline(0,-Rdom,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5); % arc de 180°, ligne brisee avec 5° de
% largeur angulaire pour chaque segment
mi_zoomnatural; % recentrer l'affichage
- Python :
femm.mi_drawline(0,-Rdom,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5) # arc de 180°, ligne brisee avec 5° de
# largeur angulaire pour chaque segment
femm.mi_zoomnatural() # recentrer l'affichage
Physique et maillage
Matériaux et sources
Pour définir les matériaux, nous avons 2 façons de procéder :
- Soit les créer avec la commande
mi_addmaterial; - Soit utiliser ceux de la bibliothèque intégrée à FEMM et les importer avec
mi_getmaterial.
Nous allons utiliser les deux :
- MATLAB :
% Definition de la physique
%-------------------------------
% Materiaux
mi_addmaterial('Air',1,1); % creation de l'air (murx = mury = 1)
mi_getmaterial('Copper'); % recuperation du cuivre
mi_modifymaterial('Copper',0,'Cuivre') % renommage
- Python :
# Definition de la physique
#-------------------------------
# Materiaux
femm.mi_addmaterial('Air',1,1) # creation de l'air (murx = mury = 1)
femm.mi_getmaterial('Copper') # recuperation du cuivre
femm.mi_modifymaterial('Copper',0,'Cuivre') # renommage
mi_addmaterialpermet de définir toutes les caractéristiques physiques du matériau (perméabilité relative, champ coercitif, conductivité électrique, etc...). Je vous encourage à regarder dans le fichier d'aide toutes les possibilités.
Il nous faut également définir le courant source circulant dans la bobine :
- MATLAB :
mi_addcircprop('I',Ic,1); % creation d'un circuit 'I' portant Ic ampères en série
- Python :
femm.mi_addcircprop('I',Ic,1) # creation d'un circuit 'I' portant Ic ampères en série
Il nous reste à affecter chaque matériau à sa région :
- MATLAB :
% taille d'elements dans regions
taille_elt_cuivre = a/5; % taille d'element globale dans bobine
taille_elt_air = Rdom/10; % ------------------- dans le domaine
mi_addblocklabel(R+a/2,0);
mi_selectlabel(R+a/2,0);
mi_setblockprop('Cuivre',0,taille_elt_cuivre,'I',0,2,N); % le 2 est le n° du groupe
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',0,taille_elt_air,0,0,1,0);
mi_clearselected;
- Python :
# taille d'elements dans regions
taille_elt_cuivre = a/5 # taille d'element globale dans bobine
taille_elt_air = Rdom/10 # ------------------- dans le domaine
femm.mi_addblocklabel(R+a/2,0)
femm.mi_selectlabel(R+a/2,0)
femm.mi_setblockprop('Cuivre',0,taille_elt_cuivre,'I',0,2,N) # le 2 est le n° du groupe
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',0,taille_elt_air,0,0,1,0)
femm.mi_clearselected()
Remarque : En procédant de cette manière, FEMM imposera ainsi une densité de courant équivalente \(j_\theta = \frac{N\,I_c}{a\,b}\) dans la bobine.
Nous avons également défini ici une taille globale d'éléments dans les deux régions. Nous aurions pu laisser le logiciel choisir tout seul une discrétisation, mais je préfère le contrôler moi-même. Nous allons donc également en profiter pour choisir une discrétisation des lignes de la bobine et de celle sur l'axe :
- MATLAB :
mi_selectsegment(R,0);
mi_selectsegment(R+a,0);
mi_selectsegment(R+a/2,b/2);
mi_selectsegment(R+a/2,-b/2);
mi_setsegmentprop(0,taille_elt_cuivre,0,0,2); % le 2 est le n° du groupe
mi_clearselected;
mi_selectsegment(0,0);
mi_setsegmentprop(0,taille_elt_air,0,0,2); % le 2 est le n° du groupe
mi_clearselected;
- Python :
femm.mi_selectsegment(R,0)
femm.mi_selectsegment(R+a,0)
femm.mi_selectsegment(R+a/2,b/2)
femm.mi_selectsegment(R+a/2,-b/2)
femm.mi_setsegmentprop('',taille_elt_cuivre,0,0,2) # le 2 est le n° du groupe
femm.mi_clearselected()
femm.mi_selectsegment(0,0)
femm.mi_setsegmentprop('',taille_elt_air,0,0,2) # le 2 est le n° du groupe
femm.mi_clearselected()
Condition à la frontière
Comme dit précédemment la condition par défaut est un champ normal à la frontière. Il nous faut donc ajouter une condition pour « forcer » le champ à rester dans le domaine : en imposant \(a_\theta = \text{constante}\) (condition de Dirichlet).
Puisque la frontière est choisie suffisamment loin pour considérer qu'il n'y a plus d'influence des sources, on imposera : \(a_\theta = 0\).
- MATLAB :
mi_addboundprop('a=0',0,0,0,0); % creation d'une CL de type Dirichlet homogene
mi_selectarcsegment(Rdom,0); % selection du bord
mi_setarcsegmentprop(5,'a=0',0,1); % affectation
% (le 5 est la largeur angulaire des segments de la ligne brisee
% representant l'arc)
- Python :
femm.mi_addboundprop('a=0',0,0,0,0) # creation d'une CL de type Dirichlet homogene
femm.mi_selectarcsegment(Rdom,0) # selection du bord
femm.mi_setarcsegmentprop(5,'a=0',0,1) # affectation
# (le 5 est la largeur angulaire des segments de la ligne brisee
# representant l'arc)
Résolution
Une fois que tout est bien défini, il ne reste plus qu'à enregistrer notre fichier *.FEM, mailler et résoudre :
- MATLAB :
mi_saveas('bobine.FEM');
mi_analyze();
- Python :
femm.mi_saveas('bobine.FEM')
femm.mi_analyze()
Post-traitement
Pour visualiser la solution, on charge le fichier résultat par :
- MATLAB :
mi_loadsolution;
- Python :
femm.mi_loadsolution()
On entre alors dans le post-processeur et toutes les commandes commenceront désormais par le préfixe mo_.
On peut alors visualiser les lignes de champ d'induction (isovaleurs de \(r\,a_\theta\)) ainsi que sa norme, par exemple :
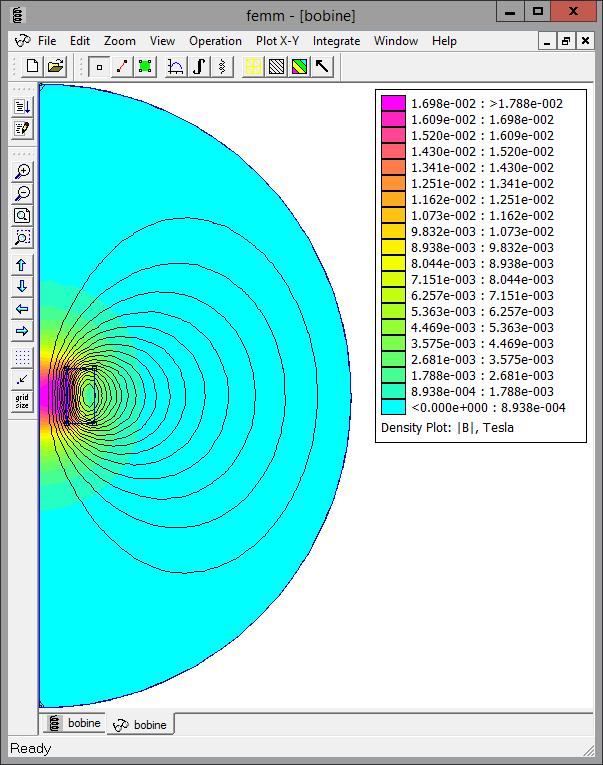
Remarque : La valeur du potentiel ou de l'induction, ne nous sert pas à grand chose en général. La plupart du temps, ce sont des grandeurs globales telles que les flux, les énergies ou les forces qui nous intéressent.
Calcul du flux et de l'inductance propre
Par le théorème de Stokes, on sait que le flux de \({\bf b}\) à travers une surface \(S_f\) est égal à la circulation de \({\bf a}\) le long du bord de la surface, soit :
\[\iint_{S_f} {\bf b}\cdot{\bf dS} = \iint_{S_f} {\bf rot\,a}\cdot{\bf dS} = \oint_{\partial S_f} {\bf a}\cdot{\bf dl}\]
On peut ainsi facilement calculer le flux traversant une spire. Par exemple pour la spire passant au point \((r_1,z_1)\) : \[\varphi = \oint\limits_{\text{spire}} {\bf a}\cdot{\bf dl} = \oint\limits_{\text{spire}} a_\theta(r_1,z_1)\,r_1\, \text{d} \theta = 2\,\pi\,r_1\,a_\theta(r_1,z_1)\]
Cette relation est valable si la section \(S_{Cu}\) de la spire est suffisamment faible pour que celle-ci soit considérée comme un circuit filiforme. Dans le cas contraire, on peut tout de même appliquer la relation précédente avec la valeur moyenne de \({a_\theta}\) sur la section.
Soit :
\[\begin{aligned}\varphi &= \oint\limits_{\text{spire}} \left( \frac{1}{S_{Cu}} \iint_{S_{Cu}} a_\theta(r,z)\,\text{d}r\,\text{d}z \right) r_1\, \text{d} \theta \\ &\simeq \oint\limits_{\text{spire}} \left( \frac{1}{S_{Cu}} \iint_{S_{Cu}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z \right) \, \text{d} \theta\\ &= \frac{2\,\pi}{S_{Cu}} \iint_{S_{Cu}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z \end{aligned}\]
En généralisant à la bobine entière, on en déduit le flux moyen traversant la bobine :
\[\varphi = \frac{2\,\pi}{S_{bob}} \iint_{S_{bob}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z\]
Avec : \(S_{bob} = a\,b\), la section de la bobine.
On obtient alors le flux total embrassé par la bobine \(\phi\) en multipliant par le nombre de spires :
\[\phi = \frac{2\,\pi\,N}{S_{bob}} \iint_{S_{bob}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z\]
Appliquons cela dès maintenant :
- MATLAB :
mo_selectblock(R+a/2,0); % selection du bloc "bobine"
S_bob = mo_blockintegral(5); % calcul de la section (alternative à a*b)
% utile si sections complexes
Integ = mo_blockintegral(1); % valeur de 2*pi*terme integral du flux moyen
phi = N*Integ/S_bob;
mo_clearblock; % deselection du block
- Python :
femm.mo_selectblock(R+a/2,0) # selection du bloc "bobine"
S_bob = femm.mo_blockintegral(5) # calcul de la section (alternative à a*b)
# utile si sections complexes
Integ = femm.mo_blockintegral(1) # valeur de 2*pi*terme integral du flux moyen
phi = N*Integ/S_bob
femm.mo_clearblock() # deselection du block
On en déduit directement l'inductance par \(\phi = L\,I_c\) :
- MATLAB :
L = phi/Ic;
disp(' Resultats');
disp('-----------------');
disp('');
disp(['Inductance de la bobine (flux) : ',num2str(L*1e6),' µH']);
- Python :
L = phi/Ic
print("")
print(" Resultats")
print("-----------------")
print(" Inductance de la bobine via le flux %.3f µH" %(L*1e6) )
Calcul de l'énergie et la coénergie magnétiques
On peut également calculer l'énergie magnétique \(W_\text{mag}\) ou la coénergie \(\widetilde{W}_\text{mag}\) stockées dans la bobine en intégrant leur densités volumiques sur tout l'espace. Elles sont, dans notre cas :
\[ w_{\text{mag}} = \frac{1}{2\,\mu_0} |\!|{\bf b}|\!|^2 , ~ ~ \text{et} ~ ~ \widetilde{w}_{\text{mag}} = \frac{1}{2}\,\mu_0\, |\!|{\bf h}|\!|^2 \]
- MATLAB :
mo_groupselectblock(); % astuce pour selectionner tous les blocs :
% on utilise une selection par groupe sans numero
Wmag = mo_blockintegral(2);
coWmag = mo_blockintegral(17);
mo_clearblock;
disp(['Energie : ',num2str(Wmag*1e3),' mJ']);
disp(['Coenergie : ',num2str(coWmag*1e3),' mJ']);
- Python :
femm.mo_groupselectblock() # astuce pour selectionner tous les blocs :
# on utilise une selection par groupe sans numero
Wmag = femm.mo_blockintegral(2)
coWmag = femm.mo_blockintegral(17)
femm.mo_clearblock()
print(" Energie : %.3f mJ" %(Wmag*1e3) )
print(" Coenergie : %.3f mJ" %(coWmag*1e3) )
Puisque nous sommes en régime linéaire, on peut également calculer l'inductance par l'énergie : \[W_\text{mag} = \frac{1}{2} L\,I_c^2\]
- MATLAB :
Lbis = 2*Wmag/Ic^2;
disp(['Inductance via l''energie : ',num2str(Lbis*1e6),' µH']);
- Python :
Lbis = 2*Wmag/Ic**2
print(" Inductance via l'energie : %.3f µH" %(Lbis*1e6) )
En linéaire, nous avons également :
\[\displaystyle W_{\text{mag}} = \iiint\limits_{\text{domaine}} \frac{1}{2}\,{\bf b}\cdot{\bf h}\,\text{d} V = \frac{1}{2} \iiint\limits_{\text{sources}} {\bf a}\cdot{\bf j}\,\text{d}V \]
On peut donc également utiliser cette formule :
- MATLAB :
mo_selectblock(R+a/2,0);
Wmagbis = 0.5*mo_blockintegral(0);
mo_clearblock;
Lbisbis = 2*Wmagbis/Ic^2;
disp(['Energie bis : ',num2str(Wmagbis*1e3),' mJ']);
disp(['Inductance via l''energie bis: ',num2str(Lbisbis*1e6),' µH']);
- Python :
Lbis = 2*Wmag/Ic**2
print(" Inductance via l'energie : %.3f µH" %(Lbis*1e6) )
femm.mo_selectblock(R+a/2,0)
Wmagbis = 0.5*femm.mo_blockintegral(0)
femm.mo_clearblock()
Lbisbis = 2*Wmagbis/Ic**2
print(" Energie bis : %.3f mJ" %(Wmagbis*1e3) )
print(" Inductance via l'energie bis: %.3f µH" %(Lbisbis*1e6) )
Au final, on obtient les résultats suivants :
Resultats
-----------------
Inductance de la bobine (flux) : 188.6474 µH
Energie : 2.3534 mJ
Coenergie : 2.3534 mJ
Inductance via l'energie : 188.2702 µH
Energie bis : 2.3581 mJ
Inductance via l'energie bis: 188.6474 µH
Les différents résultats sont très proches les uns des autres, on peut considérer que le problème est bien maillé.