Simulations de dispositifs électromagnétiques (B8-11 EC2) : Travaux Pratiques sur le logiciel FEMM

Julien Fontchastagner - v 1.2 / janv. 2024

Dernières mises à jour :

version 1.2 (raccord avec la réforme de la réforme de la réforme, 2024)
version 1.1 (raccord avec la réforme de la réforme, 2023)

Bienvenue sur le mini-site dédié aux TP FEMM de l'EC B8-11-EC2 pour les 2A ENSEM Formation Énergie.

Vous trouverez ici toutes les ressources nécessaires pour réaliser les 12 heures de séances de TP dédiées à l'utilisation du logiciel Finite Element Method Magnetics (FEMM).

Remarques :

Vous pouvez changer le thème de couleur en utilisant l'icône "pinceau" en haut à gauche.

Vous pouvez générer un document imprimable ou exportable en PDF en cliquant sur l'icône "imprimante" en haut à droite.

Pour toute remarque ou question, n'hésitez pas à me contacter par mail : julien.fontchastagner@univ-lorraine.fr.

ENSEM - Département Génie Électrique

Introduction & consignes

Présentation succincte de FEMM

FEMM, pour Finite Element Method Magnetics, est un logiciel de calcul du champ électromagnétique en 2D dans l'approximation des régimes quasi-statiques (ARQS) par la méthode des éléments finis.

C'est un logiciel en source accessible et gratuit, mais non libre (Aladdin Free Public License), développé par une seule personne : David Meeker. Le code s'appuie sur le mailleur libre Triangle et le langage de script Lua, et peut être piloté depuis un logiciel de calcul externe via son propre langage de script.

Il peut résoudre des problèmes en :

Électrostatique (Electrostatics Problem) ;
Électrocinétique (Current Flow Problem) ;
Thermique stationnaire (Heat Flow Problem) ;
Magnétostatique et magnétoharmonique (Magnetics Problem).

Pour nous, ses principaux points forts seront :

sa facilité d'utilisation ;
le fait qu'il soit dédié aux problématiques du Génie Électrique ;
sa très bonne intégration avec :
- des logiciels de calcul scientifique : GNU Octave / MATLAB, Scilab ou encore Mathematica.
- des langages de programmation : Python ou Lua.

Ses principaux inconvénients sont :

l'absence de résolution magnétique en transitoire et donc de couplage circuit ;
l'impossibilité de charger une densité de puissance non uniforme par bloc (issue d'une résolution magnétoharmonique par exemple) dans un problème de thermique ;
le fait que l'exécutable soit un binaire purement Windows (même s'il est parfaitement compatible avec Wine).

But des Travaux Pratiques

L'objectif des séances de TP est de vous apprendre à définir proprement des problèmes de magnétostatique et magnétoharmonique dans FEMM et les résoudre. Nous privilégierons l'utilisation des fonctionnalités de scriptage via MATLAB (compte-tenu que vous êtes sensés déjà connaître ce logiciel de calcul numérique), ou Python pour ceux qui préfèrent.

À l'issue des séances, vous devriez connaître les bases et certaines particularités de FEMM, et être capables de l'utiliser par la suite pour résoudre des problèmes plus compliqués ou relevant d'autres physiques.

Déroulement des séances

Les sujets ne sont pas calibrés pour correspondre à une séance particulière. Il faut voir l'ensemble des 16 heures prévues comme un unique micro-projet dans lequel seront traités les différents énoncés.

Les séances se dérouleront en salle informatique à l'ENSEM où tout ce qu'il faut est installé par défaut sur les postes de travail (FEMM, MATLAB, Python, GNU Octave).

Si, malheureusement, nous étions obligés d'effectuer les séances en mode « distanciel » via visioconférence : FEMM et MATLAB sont accessibles depuis le portail Virt'UL.

Remarque : Vous pouvez également installer sur votre PC personnel :

MATLAB avec la license campus de l'UL en suivant les instructions du WikiDocs

FEMM à partir de son site web https://www.femm.info

Python à partir de son site web https://www.python.org, puis le module PyFEMM via pip : pip3 install pyfemm

GNU Octave (en remplacement de MATLAB) à partir de son site web

Note pour les éventuels linuxiens :

Vous devrez installer FEMM avec Wine, la dernière version stable (avril 2019) fonctionne parfaitement (y compris en 64-bits), testée sans problème sous Debian ou Void.
Edit 2023 : Il peut y avoir de légers soucis avec les versions récentes de Wine (problème de DLL manquantes). Si cela vous arrive, un winetricks -q vcrun2008 dans un terminal devrait régler le problème. Demandez-moi comment faire si besoin.

Il vous faudra utiliser GNU Octave au lieu de MATLAB, et modifier les fichiers openfemm.m et callfemm.m. Voir ici.
Je vous donne une version des deux fichiers à utiliser (et à copier dans ~/.wine/drive_c/femm42/mfiles/) :openfemm.m et callfemm.m. Demandez-moi comment faire si besoin (c'est mon mode d'utilisation par défaut).

Pour ceux qui préfère Python, le module PyFEMM fonctionne parfaitement out of the box, testé sans problème sous Debian ou Void.

Note (bis) pour les maceux : il vous faudra procéder comme les linuxiens : Wine+FEMM combiné avec GNU/Octave ou Python. Si vous rencontrez des problèmes, utilisez une machine virtuelle Linux.

Pour résumé, voici les différents modes d'utilisation disponibles et possibles :

FEMM + MATLAB :

Salles infos

Virt'UL

PC personnel sous :

Windows

Linux

MacOS

FEMM + Python (PyFEMM) :

Salles infos

Virt'UL

PC personnel sous :

Windows

Linux

MacOS

FEMM + GNU/Octave :

Salles infos

Virt'UL

PC personnel sous :

Windows

Linux

MacOS

Modalités d'évaluation

Chaque étudiant sera évalué grâce à un compte-rendu unique et personnel synthétisant le travail effectué dans le cadre du micro-projet. Je vous demande d'être synthétique, et limite volontairement la taille de ce rapport à 10 pages maximum.

Faites tout de même un effort de rédaction. Un rapport, c'est : une introduction exposant la problématique, un développement du travail réalisé (pas nécessairement linéaire), et une conclusion pertinente.

Bien que le compte-rendu soit personnel, vous pouvez et êtes même encouragés à travailler en petit groupe (en binôme par exemple).

En plus du rapport, je ferai un court entretien avec chaque groupe en dernière séance, celui-ci sera évalué et permettra de moduler la note de compte-rendu.

Bonnes pratiques avant de partir tête baissée

Scripts MATLAB ou Python

Pensez à créer dans votre compte un dossier de travail (du genre TP_FEMM) et différents sous-dossiers pour chaque sujet. Depuis les salles infos, le mieux est d'utiliser un répertoire local dans C:\Temp\ et de penser à récupérer ce qu'il contient à la fin de la séance.
Pensez à indenter et commenter vos programmes.

Avec MATLAB, pensez à commencer votre programme principal par un bon nettoyage :

close all 	% fermeture de toutes les fenetres ouvertes
clear 		% suppression de toutes les variables
clc 		% purge du terminal de commande

FEMM + MATLAB

Passerelle avec MATLAB :
Dans MATLAB, ajoutez (en début de programme) le chemin vers le dossier contenant les fonctions permettant de piloter FEMM :

addpath('C:\femm42\mfiles')
% sous Linux : addpath('~/.wine/drive_c/femm42/mfiles')
% Vous pouvez éventuellement sauvegarder ce chemin 
% pour éviter de devoir le fournir à chaque fois avec 
% l'interface graphique ou la commande :
% savepath(...)

Toutes les commandes dont vous allez avoir besoin se trouvent dans un document PDF très pratique : octavefemm.pdf. Vous devez absolument l'avoir avec vous pendant les séances de TP :
- Vous le trouverez dans le dossier C:\femm42.
- Ou vous pouvez le télécharger directement depuis le site web.

FEMM + Python

Passerelle avec Python :
Importez le module PyFEMM (ainsi que NumPy et de quoi tracer des courbes) :
```
import femm
import numpy as np
import matplotlib.pyplot as plt
```
Toutes les commandes dont vous allez avoir besoin se trouvent dans un document PDF très pratique : pyfemm-manual.pdf. Vous devez absolument l'avoir avec vous pendant les séances de TP : vous pouvez le télécharger directement depuis le site web.

Astuce : Tous les bouts de code de ce site sont copiables directement en cliquant sur la petite icône en haut à droite de chaque bloc les contenant.

Tutoriels de prise en main

Nous allons commencer tranquillement en suivant un petit tutoriel fortement inspiré par celui du site officiel : Magnetics Tutorials.

Remarque : Je vous encourage d'ailleurs à suivre ce dernier en guise de préparation aux TP afin de vous approprier l'interface graphique.

Explications rapides

Nous nous intéresserons dans les premières séances à des problèmes de magnétostatique. Ainsi, en utilisant le potentiel vecteur magnétique $ {\bf a} $, la formulation forte du problème est l'équation de Maxwell-Ampère : $$ {\bf rot}\left( \nu~{\bf rot}\,{\bf a} - {\bf h_c}\right) = {\bf j} $$ Où :

$ \nu ~(= \mu^{-1}) $ est la réluctivité magnétique (inverse ou réciproque de la perméabilité) ;
${\bf h_c}$ est le champ coercitif du milieu (si c'est un aimant permanent) ;
${\bf j}$ est la densité de courant.

Les problèmes considérés seront tous 2D, et l'équation vectorielle ci-dessus se ramènera à une équation scalaire. Deux types de géométries seront étudiés :

2D plan, où : ${\bf a} = \begin{pmatrix} 0 \\ 0 \\ a_z(x,y) \end{pmatrix}$
2D axisymétrique, où : ${\bf a} = \begin{pmatrix} 0 \\ a_\theta(r,z) \\ 0 \end{pmatrix}$

Dans les deux cas, les invariants (en $z$ ou en $\theta$ ) permettent :

d'assurer implicitement la jauge de Coulomb : $$ \text{div}\,{\bf a} = 0 $$
d'obtenir la formulation forte scalaire équivalente du problème. Elle doit ressembler à quelque chose comme ci-dessous avant développement (donnée à titre purement illustratif) :
- en 2D plan :
  $$ \text{div}\,\left(\nu~{\bf grad}\,a_z - {\bf u_z}\wedge{\bf h_c}\right) + j_z = 0 $$
- en 2D axisymétrique :
  $$\text{div}\,\left(\nu~{\bf grad}\,w - {\bf u_\theta}\wedge{\bf h_c}\right) + j_\theta = 0 $$ Avec le potentiel vecteur modifié : $w\,(R = r^2, z) = r\,a_\theta\,(r,z)$

Compte-tenu de ce qui précède, le problème peut être résolu en utilisant des éléments finis triangulaires nodaux du premier ordre, où les degrés de liberté (inconnues) seront les valeurs aux nœuds des composantes $a_z$ ou $a_\theta$ du potentiel vecteur.

Ainsi, la condition aux limites par défaut (implicite) sur une frontière du domaine sera une condition de Neumann homogène : \[ \frac{\partial\,a_z}{\partial n} = 0, ~ ~ \text{ou} ~ ~ \frac{\partial\,(r\,a_\theta)}{\partial n} = 0\] Celle-ci est équivalente à une induction tangentielle nulle. Par conséquent, sauf imposition par l'utilisateur d'une condition particulière sur un des bords, le champ sera orthogonal à cette frontière par défaut (ce qui n'est généralement pas voulu).

Vous trouverez tous les compléments théoriques dans l'EC A4-EC1 « Électromagnétisme BF analytique et numérique ».

Après résolution, on déduit les valeurs des champs en appliquant l'opérateur rotationnel au potentiel vecteur et en utilisant la loi de comportement magnétique.

Étapes de résolution

Le fonctionnement du logiciel suit donc les étapes classiques d'un logiciel de calcul par éléments finis :

Preprocessing (prétraitement) : Définition de toutes les données du problème, soit :
- Définition du type de problème : magnétique 2D ou axisymétrique / statique ou harmonique / profondeur...
- Définition de la géométrie : Points / Lignes / Surfaces ;
- Définition de la physique : Matériaux / Conditions aux limites (CL) / Termes sources (courants) / Régions extérieures.
- Affectation de la physique : Définitions des régions physiques (block label), affectation des CL.
- Définition du maillage : discrétisation des lignes / tailles d'éléments dans les régions.
- Maillage : création des triangles découpant notre géométrie (éléments) et de leurs sommets (nœuds).
Solver (résolution) : calcul des valeurs de $a_z$ ou $a_\theta$ aux nœuds.
Postprocessing (post-traitement) : calculs des grandeurs annexes à partir du potentiel vecteur :
- Champ d'induction : ${\bf b} = {\bf rot\,a}$ ;
- Champ magnétique : ${\bf h} = \nu~{\bf b}$ ;
- Énergie et coénergie magnétiques ;
- Pertes Joule ;
- Flux ;
- Forces et couple.

Remarque : Les étapes de preprocessing et postprocessing sont très clairement dissociées dans FEMM et apparaissent chacune dans deux onglets différents :

le premier lié au fichier de description du problème en *.FEM.
En mode "script", toutes les instructions s'y rapportant commenceront par le préfixe mi_.

le second lié au fichier résultat en *.ans.
Et en mode "script", toutes les instructions s'y rapportant commenceront par le préfixe mo_.

Nous disposons maintenant de toutes les informations pour commencer, alors allons-y !

Premier tuto : une bobine

But du tuto : apprendre à définir un premier problème simple de magnétostatique et le résoudre.

Notions abordées :

création de la géométrie ;

définition de la physique et affectation ;

maillage et résolution ;

quelques calculs post-traitement, en particulier le flux magnétique.

On considère une bobine de fils de cuivre cylindrique, de rayon $R$, d'épaisseur $a$ et de hauteur $b$, telle que représentée sur la figure ci-dessous. Elle est constituée de $N$ spires parcourues par un courant $I_c$.

Schéma de la bobine

Le but est de calculer le champ qu'elle produit, l'énergie correspondante, ainsi que son inductance propre.

Définition du problème

Pour commencer, on crée (au bon endroit) un fichier bobine.m ou bobine.py par exemple, et on y rentre le préambule « classique » :

MATLAB :

% Fichier bobine.m simulant la bobine du premier tuto avec FEMM
close all 
clear
clc

addpath('C:\femm42\mfiles')

Python :

# Fichier bobine.py simulant la bobine du premier tuto avec FEMM
import numpy as np
import femm

On ajoute les valeurs des paramètres :

MATLAB :

% Donnes probleme
R = 10; % mm
a = 10; % mm
b = 20; % mm
N = 100;
Ic = 5; % A

% Grandeurs annexes
Rdom = 5*sqrt((R+a)^2+(b/2)^2);  % Rayon du domaine

Python :

# Donnees du probleme
R = 10.0 # mm
a = 10.0 # mm
b = 20.0 # mm
N = 100
Ic = 5.0 # A

# Grandeurs annexes
Rdom = 5*np.sqrt((R+a)**2+(b/2)**2)  # Rayon du domaine

On peut alors ouvrir FEMM :

openfemm()

femm.openfemm()

Remarque : Parfois, il peut être utile de démarrer FEMM en mode "minimisé" (pendant des procédés itératifs où on effectue plusieurs calculs de suite). On peut le faire directement par : openfemm(1)

Débutons un nouveau problème magnétique et spécifions ces propriétés :

MATLAB :

newdocument(0)  % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique

Python :

femm.newdocument(0)  # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique

Géométrie

On peut ensuite passer à la création de la géométrie. C'est un simple rectangle : on crée les quatre sommets et les quatre côtés par :

MATLAB :

% Definition de la geometrie
%-------------------------------
% Creation des points (noeuds) :
mi_addnode(R,b/2);
mi_addnode(R+a,b/2);
mi_addnode(R+a,-b/2);
mi_addnode(R,-b/2);

% Creation des segments :
mi_addsegment(R,b/2,R+a,b/2);
mi_addsegment(R+a,b/2,R+a,-b/2);
mi_addsegment(R+a,-b/2,R,-b/2);
mi_addsegment(R,-b/2,R,b/2);

Python :

# Definition de la geometrie
#-------------------------------
# Creation des points (noeuds) :
femm.mi_addnode(R,b/2)
femm.mi_addnode(R+a,b/2)
femm.mi_addnode(R+a,-b/2)
femm.mi_addnode(R,-b/2)

# Creation des segments :
femm.mi_addsegment(R,b/2,R+a,b/2)
femm.mi_addsegment(R+a,b/2,R+a,-b/2)
femm.mi_addsegment(R+a,-b/2,R,-b/2)
femm.mi_addsegment(R,-b/2,R,b/2)

Remarque : Ceci est la façon la plus basique de procéder, on aurait pu utiliser des fonctions plus évoluées comme mi_drawpolyline (MATLAB uniquement), mi_drawpolygon (MATLAB uniquement) ou, encore mieux dans notre cas, mi_drawrectangle. Pour notre rectangle, on aurait donc pu faire :

mi_drawpolyline([R,b/2;R+a,b/2;R+a,-b/2;R,-b/2;R,b/2]) (MATLAB)

mi_drawpolygon([R,b/2;R+a,b/2;R+a,-b/2;R,-b/2]) (MATLAB)

mi_drawrectangle(R,b/2,R+a,-b/2) (MATLAB ou Python)

Ce qui est évidemment beaucoup plus compact...

Pour le domaine d'air environnant, nous allons définir un demi-disque de rayon Rdom :

MATLAB :

mi_drawline(0,-Rdom,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5);  % arc de 180°, ligne brisee avec 5° de
								  % largeur angulaire pour chaque segment
mi_zoomnatural;  % recentrer l'affichage

Python :

femm.mi_drawline(0,-Rdom,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5)  # arc de 180°, ligne brisee avec 5° de
                                      # largeur angulaire pour chaque segment
femm.mi_zoomnatural()  # recentrer l'affichage

Physique et maillage

Matériaux et sources

Pour définir les matériaux, nous avons 2 façons de procéder :

Soit les créer avec la commande mi_addmaterial ;
Soit utiliser ceux de la bibliothèque intégrée à FEMM et les importer avec mi_getmaterial.

Nous allons utiliser les deux :

MATLAB :

% Definition de la physique
%-------------------------------

% Materiaux
mi_addmaterial('Air',1,1);  % creation de l'air (murx = mury = 1)
mi_getmaterial('Copper');   % recuperation du cuivre
mi_modifymaterial('Copper',0,'Cuivre') % renommage

Python :

# Definition de la physique
#-------------------------------

# Materiaux
femm.mi_addmaterial('Air',1,1)   # creation de l'air (murx = mury = 1)
femm.mi_getmaterial('Copper')    # recuperation du cuivre
femm.mi_modifymaterial('Copper',0,'Cuivre')   # renommage

mi_addmaterial permet de définir toutes les caractéristiques physiques du matériau (perméabilité relative, champ coercitif, conductivité électrique, etc...). Je vous encourage à regarder dans le fichier d'aide toutes les possibilités.

Il nous faut également définir le courant source circulant dans la bobine :

MATLAB :

mi_addcircprop('I',Ic,1); % creation d'un circuit 'I' portant Ic ampères en série

Python :

femm.mi_addcircprop('I',Ic,1)   # creation d'un circuit 'I' portant Ic ampères en série

Il nous reste à affecter chaque matériau à sa région :

MATLAB :

% taille d'elements dans regions
taille_elt_cuivre = a/5;  % taille d'element globale dans bobine
taille_elt_air = Rdom/10; %   -------------------  dans le domaine

mi_addblocklabel(R+a/2,0);
mi_selectlabel(R+a/2,0);
mi_setblockprop('Cuivre',0,taille_elt_cuivre,'I',0,2,N); % le 2 est le n° du groupe
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',0,taille_elt_air,0,0,1,0);
mi_clearselected;

Python :

# taille d'elements dans regions
taille_elt_cuivre = a/5  # taille d'element globale dans bobine
taille_elt_air = Rdom/10 #   -------------------  dans le domaine

femm.mi_addblocklabel(R+a/2,0)
femm.mi_selectlabel(R+a/2,0)
femm.mi_setblockprop('Cuivre',0,taille_elt_cuivre,'I',0,2,N) # le 2 est le n° du groupe
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',0,taille_elt_air,0,0,1,0)
femm.mi_clearselected()

Remarque : En procédant de cette manière, FEMM imposera ainsi une densité de courant équivalente $j_\theta = \frac{N\,I_c}{a\,b}$ dans la bobine.

Nous avons également défini ici une taille globale d'éléments dans les deux régions. Nous aurions pu laisser le logiciel choisir tout seul une discrétisation, mais je préfère le contrôler moi-même. Nous allons donc également en profiter pour choisir une discrétisation des lignes de la bobine et de celle sur l'axe :

MATLAB :

mi_selectsegment(R,0);
mi_selectsegment(R+a,0);
mi_selectsegment(R+a/2,b/2);
mi_selectsegment(R+a/2,-b/2);
mi_setsegmentprop(0,taille_elt_cuivre,0,0,2); % le 2 est le n° du groupe
mi_clearselected;
mi_selectsegment(0,0);
mi_setsegmentprop(0,taille_elt_air,0,0,2); % le 2 est le n° du groupe
mi_clearselected;

Python :

femm.mi_selectsegment(R,0)
femm.mi_selectsegment(R+a,0)
femm.mi_selectsegment(R+a/2,b/2)
femm.mi_selectsegment(R+a/2,-b/2)
femm.mi_setsegmentprop('',taille_elt_cuivre,0,0,2)  # le 2 est le n° du groupe
femm.mi_clearselected()
femm.mi_selectsegment(0,0)
femm.mi_setsegmentprop('',taille_elt_air,0,0,2)  # le 2 est le n° du groupe
femm.mi_clearselected()

Condition à la frontière

Comme dit précédemment la condition par défaut est un champ normal à la frontière. Il nous faut donc ajouter une condition pour « forcer » le champ à rester dans le domaine : en imposant $a_\theta = \text{constante}$ (condition de Dirichlet).

Puisque la frontière est choisie suffisamment loin pour considérer qu'il n'y a plus d'influence des sources, on imposera : $a_\theta = 0$.

MATLAB :

mi_addboundprop('a=0',0,0,0,0); % creation d'une CL de type Dirichlet homogene
mi_selectarcsegment(Rdom,0);         % selection du bord
mi_setarcsegmentprop(5,'a=0',0,1);  % affectation 
		% (le 5 est la largeur angulaire des segments de la ligne brisee
		% representant l'arc)

Python :

femm.mi_addboundprop('a=0',0,0,0,0)  # creation d'une CL de type Dirichlet homogene
femm.mi_selectarcsegment(Rdom,0)         # selection du bord
femm.mi_setarcsegmentprop(5,'a=0',0,1)   # affectation 
        # (le 5 est la largeur angulaire des segments de la ligne brisee
        # representant l'arc)

Résolution

Une fois que tout est bien défini, il ne reste plus qu'à enregistrer notre fichier *.FEM, mailler et résoudre :

MATLAB :

mi_saveas('bobine.FEM');
mi_analyze();

Python :

femm.mi_saveas('bobine.FEM')
femm.mi_analyze()

Post-traitement

Pour visualiser la solution, on charge le fichier résultat par :

MATLAB :

mi_loadsolution;

Python :

femm.mi_loadsolution()

On entre alors dans le post-processeur et toutes les commandes commenceront désormais par le préfixe mo_.

On peut alors visualiser les lignes de champ d'induction (isovaleurs de $r\,a_\theta$) ainsi que sa norme, par exemple :

Resultat

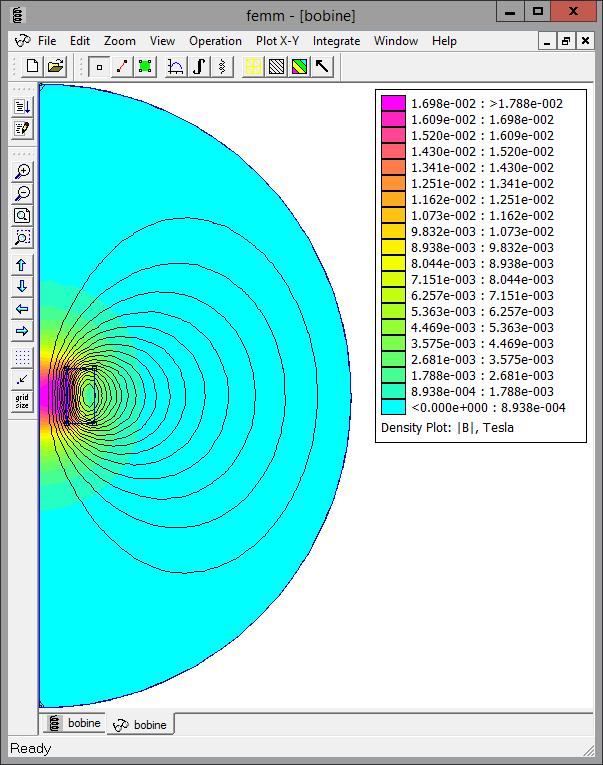
Remarque : La valeur du potentiel ou de l'induction, ne nous sert pas à grand chose en général. La plupart du temps, ce sont des grandeurs globales telles que les flux, les énergies ou les forces qui nous intéressent.

Calcul du flux et de l'inductance propre

Par le théorème de Stokes, on sait que le flux de ${\bf b}$ à travers une surface $S_f$ est égal à la circulation de ${\bf a}$ le long du bord de la surface, soit :

\[\iint_{S_f} {\bf b}\cdot{\bf dS} = \iint_{S_f} {\bf rot\,a}\cdot{\bf dS} = \oint_{\partial S_f} {\bf a}\cdot{\bf dl}\]

On peut ainsi facilement calculer le flux traversant une spire. Par exemple pour la spire passant au point $(r_1,z_1)$ : \[\varphi = \oint\limits_{\text{spire}} {\bf a}\cdot{\bf dl} = \oint\limits_{\text{spire}} a_\theta(r_1,z_1)\,r_1\, \text{d} \theta = 2\,\pi\,r_1\,a_\theta(r_1,z_1)\]

Cette relation est valable si la section $S_{Cu}$ de la spire est suffisamment faible pour que celle-ci soit considérée comme un circuit filiforme. Dans le cas contraire, on peut tout de même appliquer la relation précédente avec la valeur moyenne de ${a_\theta}$ sur la section.
Soit :

\[\begin{aligned}\varphi &= \oint\limits_{\text{spire}} \left( \frac{1}{S_{Cu}} \iint_{S_{Cu}} a_\theta(r,z)\,\text{d}r\,\text{d}z \right) r_1\, \text{d} \theta \\ &\simeq \oint\limits_{\text{spire}} \left( \frac{1}{S_{Cu}} \iint_{S_{Cu}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z \right) \, \text{d} \theta\\ &= \frac{2\,\pi}{S_{Cu}} \iint_{S_{Cu}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z \end{aligned}\]

En généralisant à la bobine entière, on en déduit le flux moyen traversant la bobine :

\[\varphi = \frac{2\,\pi}{S_{bob}} \iint_{S_{bob}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z\]

Avec : $S_{bob} = a\,b$, la section de la bobine.

On obtient alors le flux total embrassé par la bobine $\phi$ en multipliant par le nombre de spires :

\[\phi = \frac{2\,\pi\,N}{S_{bob}} \iint_{S_{bob}} r\,a_\theta(r,z)\,\text{d}r\,\text{d}z\]

Appliquons cela dès maintenant :

MATLAB :

mo_selectblock(R+a/2,0);  % selection du bloc "bobine"
S_bob = mo_blockintegral(5); % calcul de la section (alternative à a*b)
							% utile si sections complexes
Integ = mo_blockintegral(1);  % valeur de 2*pi*terme integral du flux moyen
phi = N*Integ/S_bob;
mo_clearblock;  % deselection du block

Python :

femm.mo_selectblock(R+a/2,0)  # selection du bloc "bobine"
S_bob = femm.mo_blockintegral(5) # calcul de la section (alternative à a*b)
                            # utile si sections complexes
Integ = femm.mo_blockintegral(1) # valeur de 2*pi*terme integral du flux moyen
phi = N*Integ/S_bob
femm.mo_clearblock() # deselection du block

On en déduit directement l'inductance par $\phi = L\,I_c$ :

MATLAB :

L = phi/Ic;
disp(' Resultats');
disp('-----------------');
disp('');
disp(['Inductance de la bobine (flux) : ',num2str(L*1e6),' µH']);

Python :

L = phi/Ic
print("")
print(" Resultats")
print("-----------------")
print(" Inductance de la bobine via le flux %.3f µH" %(L*1e6) )

Calcul de l'énergie et la coénergie magnétiques

On peut également calculer l'énergie magnétique $W_\text{mag}$ ou la coénergie $\widetilde{W}_\text{mag}$ stockées dans la bobine en intégrant leur densités volumiques sur tout l'espace. Elles sont, dans notre cas :

\[ w_{\text{mag}} = \frac{1}{2\,\mu_0} |\!|{\bf b}|\!|^2 , ~ ~ \text{et} ~ ~ \widetilde{w}_{\text{mag}} = \frac{1}{2}\,\mu_0\, |\!|{\bf h}|\!|^2 \]

MATLAB :

mo_groupselectblock();   % astuce pour selectionner tous les blocs :
						% on utilise une selection par groupe sans numero
Wmag = mo_blockintegral(2); 
coWmag = mo_blockintegral(17);
mo_clearblock;
disp(['Energie : ',num2str(Wmag*1e3),' mJ']);
disp(['Coenergie : ',num2str(coWmag*1e3),' mJ']);

Python :

femm.mo_groupselectblock()   # astuce pour selectionner tous les blocs :
                        # on utilise une selection par groupe sans numero
Wmag = femm.mo_blockintegral(2)
coWmag = femm.mo_blockintegral(17)
femm.mo_clearblock()
print(" Energie : %.3f mJ" %(Wmag*1e3) )
print(" Coenergie : %.3f mJ" %(coWmag*1e3) )

Puisque nous sommes en régime linéaire, on peut également calculer l'inductance par l'énergie : \[W_\text{mag} = \frac{1}{2} L\,I_c^2\]

MATLAB :

Lbis = 2*Wmag/Ic^2;
disp(['Inductance via l''energie : ',num2str(Lbis*1e6),' µH']);

Python :

Lbis = 2*Wmag/Ic**2
print(" Inductance via l'energie : %.3f µH" %(Lbis*1e6) )

En linéaire, nous avons également :

\[\displaystyle W_{\text{mag}} = \iiint\limits_{\text{domaine}} \frac{1}{2}\,{\bf b}\cdot{\bf h}\,\text{d} V = \frac{1}{2} \iiint\limits_{\text{sources}} {\bf a}\cdot{\bf j}\,\text{d}V \]

On peut donc également utiliser cette formule :

MATLAB :

mo_selectblock(R+a/2,0); 
Wmagbis = 0.5*mo_blockintegral(0); 
mo_clearblock;
Lbisbis = 2*Wmagbis/Ic^2;
disp(['Energie bis : ',num2str(Wmagbis*1e3),' mJ']);
disp(['Inductance via l''energie bis: ',num2str(Lbisbis*1e6),' µH']);

Python :

Lbis = 2*Wmag/Ic**2
print(" Inductance via l'energie : %.3f µH" %(Lbis*1e6) )
femm.mo_selectblock(R+a/2,0) 
Wmagbis = 0.5*femm.mo_blockintegral(0)
femm.mo_clearblock()
Lbisbis = 2*Wmagbis/Ic**2
print(" Energie bis : %.3f mJ" %(Wmagbis*1e3) )
print(" Inductance via l'energie bis: %.3f µH" %(Lbisbis*1e6) )

Au final, on obtient les résultats suivants :

 Resultats
-----------------
Inductance de la bobine (flux) : 188.6474 µH
Energie : 2.3534 mJ
Coenergie : 2.3534 mJ
Inductance via l'energie : 188.2702 µH
Energie bis : 2.3581 mJ
Inductance via l'energie bis: 188.6474 µH

Les différents résultats sont très proches les uns des autres, on peut considérer que le problème est bien maillé.

Deuxième tuto : un aimant

But du tuto : apprendre à définir un aimant et connaître les différentes façons de modéliser une frontière lointaine.

Notions abordées :

définition d'un aimant permanent ;

techniques particulières pour la frontière du domaine :

transformation de Kelvin

« frontière ouverte » / boîte infinie.

Nous poursuivons nos tutos d'apprentissage avec un exemple tout aussi simple d'un point de vue géométrique : un aimant permanent cylindrique dans l'air. On prendra des dimensions similaires à celles de l'intérieur de la bobine précédente : rayon $R$, hauteur $b$. L'induction rémanente de l'aimant, polarisé axialement, est $B_r = 1,2\,\text{T}$, et sa perméabilté relative est $\mu_r = 1,05$.

Méthode « classique »

Le début du programme sera donc identique au précédent. Dans un fichier aimant.m, on rentre :

MATLAB :

% Fichier aimant.m simulant l'aimant du second tuto avec FEMM
close all 
clear
clc

addpath('C:\femm42\mfiles')

% Donnes probleme
R = 10; % mm
b = 20; % mm
Rdom = 10*sqrt(R^2+(b/2)^2); % on prend un domaine tres large

openfemm()
newdocument(0)  % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique

% Geometrie
mi_drawrectangle(0,b/2,R,-b/2);   % aimant
% domaine :
mi_addnode(0,-Rdom);
mi_addnode(0,Rdom);
mi_addsegment(0,-Rdom,0,-b/2);
mi_addsegment(0,b/2,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5); 
mi_zoomnatural;

Python :

# Fichier aimant.py simulant l'aimant du second tuto avec FEMM
import numpy as np
import femm


# Donnes probleme
R = 10 # mm
b = 20 # mm
Rdom = 10*np.sqrt(R**2+(b/2)**2) # on prend un domaine tres large

femm.openfemm()
femm.newdocument(0)  # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique

# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2)   # aimant
# domaine :
femm.mi_addnode(0,-Rdom)
femm.mi_addnode(0,Rdom)
femm.mi_addsegment(0,-Rdom,0,-b/2)
femm.mi_addsegment(0,b/2,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5) 
femm.mi_zoomnatural()

Dans un premier temps, nous choisissons un domaine très large : 10 fois la diagonale du bloc "aimant", pour être certain de ne pas dénaturer le problème.

Il nous faut maintenant définir les matériaux. Dans FEMM, un aimant permanent est caractérisé par :

sa perméabilité relative $\mu_r$,
son champ coercitif $H_c$ en $\text{A}\cdot\text{m}^{-1}$,
la direction de son aimantation (angle par rapport à l'axe des abscisses en degrés).

La courbe $B(H)$ d'un aimant peut se représenter de la façon suivante : B(H) aimant

FEMM utilise la droite passant par $(-H_c, 0)$ et $(0,B_r)$. On voit alors directement que : \[H_c = \frac{B_r}{\mu_0\,\mu_r}\]

Finalement, on peut créer nos matériaux et les affecter aux régions correspondantes. Et on ajoute la condition aux limites de Dirichlet sur le bord :

MATLAB :

Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);

mi_addmaterial('Air',1,1); 
mi_addmaterial('Aimant',mur,mur,Hc); 

mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0);  % automesh, 90° pour aimantion, groupe 2
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',1,0,0,0,1,0);  % automesh, groupe 1
mi_clearselected;

mi_addboundprop('a=0',0,0,0,0);  
mi_selectarcsegment(Rdom,0); 
mi_setarcsegmentprop(5,'a=0',0,1); 
mi_clearselected;

mi_saveas('aimant.FEM');

Python :

Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)

femm.mi_addmaterial('Air',1,1) 
femm.mi_addmaterial('Aimant',mur,mur,Hc) 

femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0)  # automesh, 90° pour aimantion, groupe 2
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0)  # automesh, groupe 1
femm.mi_clearselected()

femm.mi_addboundprop('a=0',0,0,0,0)  
femm.mi_selectarcsegment(Rdom,0) 
femm.mi_setarcsegmentprop(5,'a=0',0,1) 
femm.mi_clearselected()

femm.mi_saveas('aimant.FEM')

Nous avons volontairement laissé le choix de discrétisation automatique (automesh) pour voir.

On peut alors résoudre, visualiser les résultats et calculer l'énergie magnétique due à l'aimant :

MATLAB :

mi_analyze();
mi_loadsolution;

mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;

Python :

femm.mi_analyze()
femm.mi_loadsolution()

femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()

➤ Observez l'inversion de la direction de ${\bf h}$ dans l'aimant avec le tracé de vecteurs (densifiez la grille de tracé si besoin en cliquant sur l'icône "grid size" ou avec un mi_setgrid(R/10,'cart') par exemple), ainsi que l'ordre de grandeur de l'énergie par rapport à celle de la bobine précédente.

Remarque : Pour le calcul de l'énergie (ou de la coénergie) dans l'aimant, je vous renvoie à la page dédiée sur le Wiki de FEMM qui l'explique très bien. On retiendra que, pour un aimant, on peut utiliser : \[ w_{\text{mag}} = \frac{1}{2}\,\mu\, |\!|{\bf h}|\!|^2, ~ ~ \text{et} ~ ~ \widetilde{w}_{\text{mag}} = \frac{1}{2\,\mu} |\!|{\bf b}|\!|^2 \]

On peut constater l'intérêt de prendre un domaine assez large en comparant les valeurs d'énergie calculées pour différents rayons de domaine (Rdom) :

Rdom	Wmag (en J)	écart
$20\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,125	référence
$10\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,115	-0,9 %
$5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,118	-0,6 %
$2\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,257	11,7 %
$1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,467	30,4 %

En général, 5 fois la longueur caractéristique du dispositif est suffisante.

Sur notre exemple, on obtient la distribution de champ suivante :

Induction de l'aimant

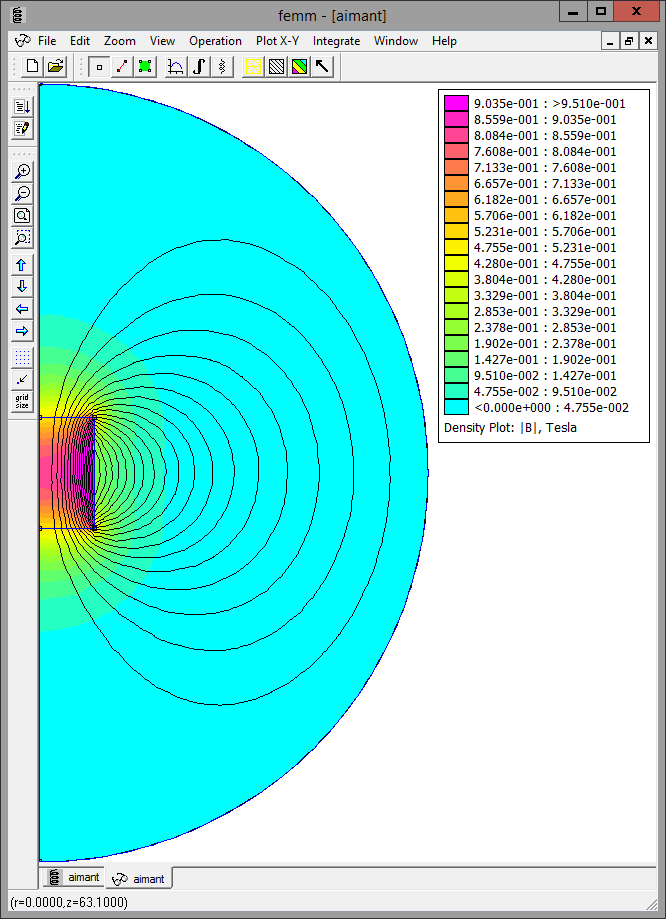
Cependant, pour de gros problèmes basés sur des géométries complexes nécessitant de nombreux éléments, il peut être intéressant de réduire le domaine d'étude afin de réduire la taille du système à résoudre (et donc le temps de calcul). FEMM dispose de deux techniques le permettant : nous allons donc les tester.

Transformation de Kelvin

Reprenons le problème précédent en le modifiant légèrement. Le rayon du domaine Rdom est réduit et nous ajoutons au dessus de celui-ci une petite sphère de rayon Rext.

MATLAB :

% Fichier aimant_TK.m simulant l'aimant du second tuto avec FEMM 
% Version avec transfo de Kelvin (region exterieure)
close all 
clear
clc

addpath('C:\femm42\mfiles')

% Donnes probleme
R = 10; % mm
b = 20; % mm
Rdom = 2*sqrt(R^2+(b/2)^2); % on prend un domaine reduit
Rext = Rdom/4;              % rayon region exterieure

openfemm()
newdocument(0)  % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique

% Geometrie
mi_drawrectangle(0,b/2,R,-b/2);   % aimant
% domaine :
mi_addnode(0,-Rdom);
mi_addnode(0,Rdom);
mi_addsegment(0,-Rdom,0,-b/2);
mi_addsegment(0,b/2,0,Rdom);
mi_addarc(0,-Rdom,0,Rdom,180,5); 
% region exterireure :
mi_addnode(0,Rdom+2*Rext);
mi_addsegment(0,Rdom,0,Rdom+2*Rext);
mi_addarc(0,Rdom,0,Rdom+2*Rext,180,5); 
mi_zoomnatural;

Python :

# Fichier aimant_TK.py simulant l'aimant du second tuto avec FEMM 
# Version avec transfo de Kelvin (region exterieure)

import numpy as np
import femm


# Donnes probleme
R = 10 # mm
b = 20 # mm
Rdom = 2*np.sqrt(R**2+(b/2)**2) # on prend un domaine reduit
Rext = Rdom/4                   # rayon region exterieure

femm.openfemm()
femm.newdocument(0)  # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique

# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2)   # aimant
# domaine :
femm.mi_addnode(0,-Rdom)
femm.mi_addnode(0,Rdom)
femm.mi_addsegment(0,-Rdom,0,-b/2)
femm.mi_addsegment(0,b/2,0,Rdom)
femm.mi_addarc(0,-Rdom,0,Rdom,180,5) 
# region exterireure :
femm.mi_addnode(0,Rdom+2*Rext)
femm.mi_addsegment(0,Rdom,0,Rdom+2*Rext)
femm.mi_addarc(0,Rdom,0,Rdom+2*Rext,180,5) 
femm.mi_zoomnatural()

Nous créons ensuite nos matériaux comme précédemment, mais en plus nous ajoutons ce que FEMM appelle une « région extérieure » associée à notre problème et que nous lions à notre petite sphère (définie comme de l'air environnant).

MATLAB :

Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);

mi_addmaterial('Air',1,1); 
mi_addmaterial('Aimant',mur,mur,Hc); 
mi_defineouterspace(Rdom+Rext/2,Rext,Rdom);     % region exterieure 

mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0);  % automesh, 90° pour aimantion, groupe 2
mi_clearselected;
mi_addblocklabel(Rdom/2,0);
mi_selectlabel(Rdom/2,0);
mi_setblockprop('Air',1,0,0,0,1,0);  % automesh, groupe 1
mi_clearselected;

mi_addblocklabel(Rext,Rdom+Rext);
mi_selectlabel(Rext/2,Rdom+Rext);
mi_setblockprop('Air',1,0,0,0,1,0);  % automesh, groupe 1
mi_attachouterspace;                 % dans region exterieure
mi_clearselected;

Python :

Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)

femm.mi_addmaterial('Air',1,1) 
femm.mi_addmaterial('Aimant',mur,mur,Hc) 
femm.mi_defineouterspace(Rdom+Rext/2,Rext,Rdom)     # region exterieure 

femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0)  # automesh, 90° pour aimantion, groupe 2
femm.mi_clearselected()
femm.mi_addblocklabel(Rdom/2,0)
femm.mi_selectlabel(Rdom/2,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0)  # automesh, groupe 1
femm.mi_clearselected()

femm.mi_addblocklabel(Rext,Rdom+Rext)
femm.mi_selectlabel(Rext/2,Rdom+Rext)
femm.mi_setblockprop('Air',1,0,0,0,1,0)  # automesh, groupe 1
femm.mi_attachouterspace()               # dans region exterieure
femm.mi_clearselected()

Il ne reste plus qu'à créer une condition de périodicité liant le bord du domaine à celui de la région extérieure.

MATLAB :

% condition de periodicite :
mi_addboundprop('Periodique',0,0,0,0,0,0,0,0,4); 
mi_selectarcsegment(Rdom,0);         % bord domaine
mi_selectarcsegment(Rext,Rdom+Rext); % bord region exterieure
mi_setarcsegmentprop(5,'Periodique',0,1); 
mi_clearselected;

mi_saveas('aimant.FEM');

Python :

# condition de periodicite :
femm.mi_addboundprop('Periodique',0,0,0,0,0,0,0,0,4) 
femm.mi_selectarcsegment(Rdom,0)         # bord domaine
femm.mi_selectarcsegment(Rext,Rdom+Rext) # bord region exterieure
femm.mi_setarcsegmentprop(5,'Periodique',0,1) 
femm.mi_clearselected()

femm.mi_saveas('aimant.FEM')

Comment ça marche ?

Dans la région extérieure, la formulation a été modifiée par un changement de variable $r \mapsto R$ tel que $\frac{1}{R} \to 0$ lorsqu'on s'approche du centre de la petite sphère. Ainsi, le centre de la région est équivalent à l'$\infty$. Le lien avec le domaine d'étude est assuré par une condition de périodicité égalisant les valeurs de $a_\theta$ sur leurs frontières respectives. Pour simplifier : tout se passe comme si on avait « replié » la partie de l'espace située en dehors du domaine d'étude dans la petite sphère du dessus.

On peut ensuite résoudre notre problème et calculer l'énergie :

MATLAB :

mi_analyze();
mi_loadsolution;

mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;

Python :

femm.mi_analyze()
femm.mi_loadsolution()

femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()

Calculons l'énergie pour les deux dernières valeurs de Rdom du paragraphe précédent :

Rdom (avec TK)	Wmag (en J)	écart avec la référence
$2\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,121	-0,4 %
$1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,144	1,7 %

Un exemple de résultats obtenus est montré sur la figure ci-dessous représentant l'induction :

Induction cas transfo Kelvin

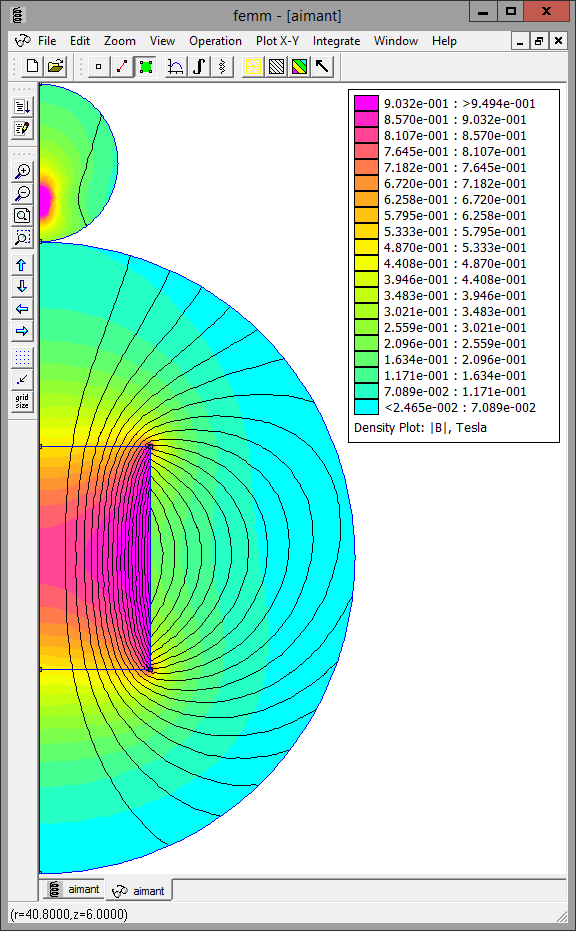
On voit clairement l'efficacité de la méthode.

Frontière ouverte (~ boîte infinie)

Une autre technique permettant de réduire le domaine d'étude est d'utiliser une condition de « frontière ouverte ». L'idée est de se rapprocher du fonctionnement d'une boîte infinie via l'utilisation de ce que l'auteur du logiciel appelle « une condition au limite asymptotique improvisée » (Improvised Asymptotic Boundary Conditions).

Contrairement à une vraie boîte infinie où l'expression du jacobien dans les bords de la boîte est modifié pour correspondre à un domaine non borné, FEMM utilise une boîte circulaire dont le bord est constitué de plusieurs couches où les valeurs de perméabilités sont modifiées pour correspondre à différents développements asymptotiques du potentiel vecteur 2D successifs. Voir ici pour plus de détails.

Même si cette technique est moins rigoureuse, mathématiquement parlant, que la transformation de Kelvin ou une vraie boîte infinie, elle fournie de très bons résultats et est surtout très facile à implanter dans FEMM :

pas besoin de créer le domaine,
pas besoin de créer une condition au limite particulière,
une seule instruction : mi_makeABC(); (les options par défaut sont, la plupart du temps, très bien choisies).

Le script pour résoudre complètement notre problème devient ainsi plus concis :

MATLAB :

% Fichier aimant_OB.m simulant l'aimant du second tuto avec FEMM 
% Version avec condition « open boundary »
close all 
clear
clc

addpath('C:\femm42\mfiles')

% Donnes probleme
R = 10; % mm
b = 20; % mm

openfemm()
newdocument(0)  % nouveau pbm magnetique
mi_probdef(0,'millimeters','axi'); % frequence = 0, en mm, axisymetrique

% Geometrie
mi_drawrectangle(0,b/2,R,-b/2); % aimant
mi_makeABC();                   % domaine (open boudary)
mi_zoomnatural;

% Physique
Br = 1.2; % T
mu0 = 4e-7*pi;
mur = 1.05;
Hc = Br/(mu0*mur);

mi_addmaterial('Air',1,1); 
mi_addmaterial('Aimant',mur,mur,Hc); 

mi_addblocklabel(R/2,0);
mi_selectlabel(R/2,0);
mi_setblockprop('Aimant',1,0,0,90,2,0); 
mi_clearselected;
mi_addblocklabel(1.2*R,0);
mi_selectlabel(1.2*R,0);
mi_setblockprop('Air',1,0,0,0,1,0); 
mi_clearselected;

mi_saveas('aimant.FEM')

mi_analyze();
mi_loadsolution;

mo_groupselectblock();
Wmag = mo_blockintegral(2);
mo_clearblock;

Python :

# Fichier aimant_OB.py simulant l'aimant du second tuto avec FEMM 
# Version avec condition « open boundary »

import numpy as np
import femm


# Donnes probleme
R = 10 # mm
b = 20 # mm

femm.openfemm()
femm.newdocument(0)  # nouveau pbm magnetique
femm.mi_probdef(0,'millimeters','axi') # frequence = 0, en mm, axisymetrique

# Geometrie
femm.mi_drawrectangle(0,b/2,R,-b/2) # aimant
femm.mi_makeABC()                   # domaine (open boudary)
femm.mi_zoomnatural()

# Physique
Br = 1.2 # T
mu0 = 4e-7*np.pi
mur = 1.05
Hc = Br/(mu0*mur)

femm.mi_addmaterial('Air',1,1) 
femm.mi_addmaterial('Aimant',mur,mur,Hc) 

femm.mi_addblocklabel(R/2,0)
femm.mi_selectlabel(R/2,0)
femm.mi_setblockprop('Aimant',1,0,0,90,2,0) 
femm.mi_clearselected()
femm.mi_addblocklabel(1.2*R,0)
femm.mi_selectlabel(1.2*R,0)
femm.mi_setblockprop('Air',1,0,0,0,1,0) 
femm.mi_clearselected()

femm.mi_saveas('aimant.FEM')

femm.mi_analyze()
femm.mi_loadsolution()

femm.mo_groupselectblock()
Wmag = femm.mo_blockintegral(2)
femm.mo_clearblock()

On obtient alors les résultats décrits par la figure et la table ci-dessous :

Aimant

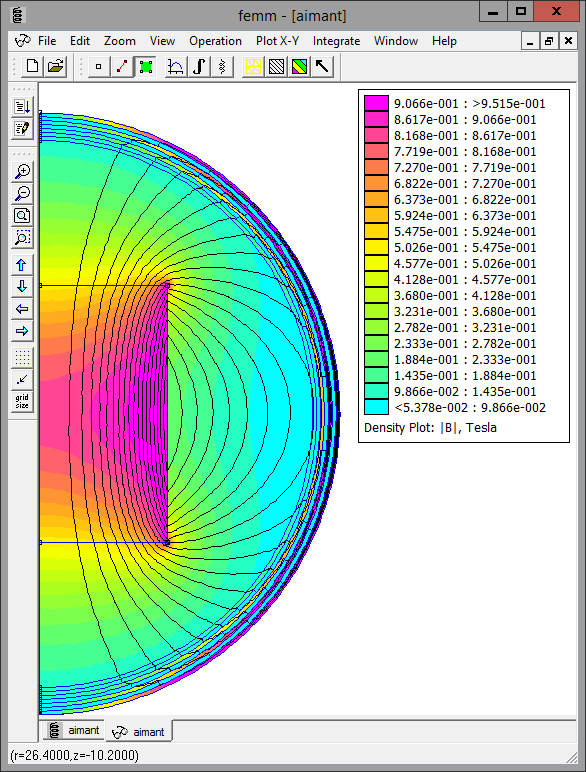
Rdom (open boundary)	Wmag (en J)	écart avec la référence
$\approx 1,5\times\sqrt{R^2+\left(\frac{b}{2}\right)^2}$	1,102	-2,0 %

Ce qui est tout à fait acceptable.

Ventouse magnétique

But du sujet : Étudier et calculer la force d'un électroaimant de type « ventouse magnétique » (verrouillage magnétique de porte).

Notions abordées :

Problème 2D Plan,

Définition des matériaux ferromagnétiques en linéaire et non-linéaire,

Calculs de force (Tenseur de Maxwell, Tenseur moyenné, dérivation de la coénergie).

Nous allons maintenant nous intéresser à un dispositif particulièrement répandu en électrotechnique : un électroaimant. L'application visée est une ventouse magnétique servant à verrouiller une porte de Hall d'immeuble ou d'hôpital par exemple. Un exemple de produit fini est donnée par la figure ci-dessous (vous pouvez passer le voir, il est dans mon bureau : 110 Rouge) :

Ventouse

Le circuit magnétique en E sur lequel il est construit, est :

Circuit magnétique ventouse

On remarquera qu'il est constitué de tôles feuilletées même si, pour ce type d'application alimentée en continu, ça ne sert à rien.

Une représentation schématique du dispositif est alors :

Schéma dispositif

Premières simulations en régime linéaire

➤ Créez le script MATLAB ou Python permettant de résoudre ce problème en linéaire.

Les valeurs des paramètres sont données par la table suivante :

Paramètres	Unité	Valeurs
aE	cm	1
bE	cm	1
hE	cm	2
e	mm	1
Ep	cm	1,5
Lz	cm	20
Ic	A	0,5
N	-	250

Remarque : Pensez à définir votre problème comme 2D cartésien de profondeur Lz.

MATLAB :
mi_probdef(0,'millimeters','planar',1e-8,Lz);  % 1e-8 = precision du solveur
Python :
femm.mi_probdef(0,'millimeters','planar',1e-8,Lz) # 1e-8 = precision du solveur

Et les matériaux magnétiques sont définis par celle-ci :

Matériau	Type	Nom	Nom FEMM	$\mu_r$
Circuit magnétique	Tôles	M530	M-45 Steel	4689
Plaque	Massif	C10	1010 Steel	902

Astuce : Dans FEMM, vous pouvez définir un retour de courant en affectant un nombre de tours négatif à un bloc associé à un circuit.

Compléments sur le calcul de force

Pour calculer les forces s'exerçant sur les pièces mobiles, FEMM utilise le tenseur des contraintes électromagnétique de Maxwell.

Le terme général de celui-ci dans l'air (contribution purement magnétique) est : \[T_{i\,k} = \frac{1}{\mu_0}\,b_i\,b_k -\frac{\delta_{i k}}{2\,\mu_0}|\!|{\bf b}|\!|^2 ~ ; ~ ~ ~ i,k = x,y,z\]

Dans notre cas particulier, l'expression du tenseur est : \[\overline{\overline{{\bf T}}} = \frac{1}{2\,\mu_0}\begin{pmatrix}b_x^2-b_y^2 & 2\, b_x b_y & 0 \\ 2\,b_x b_y & b_y^2-b_x^2 & 0 \\ 0 & 0 & - (b_x^2 + b_y^2 )\end{pmatrix}\]

On déduit la force par :

\[ {\bf F} = \iint_{S}\,\overline{\overline{{\bf T}}}\cdot{\bf d S}\]

Où $S$ est une surface fermée située dans l'air et entourant la pièce mobile. Puisque notre problème est 2D, cette surface sera représentée par un parallélépipède rectangle (pavé droit) de longueur $L_z$ et s'appuyant sur un contour fermé $C$, et :

\[ {\bf F} = L_z\,\oint_{C}\,\overline{\overline{{\bf T}}}\cdot{\bf n}\, \text{d}l\]

Dans FEMM, vous pourrez :

Créer un contour d'intégration en utilisant récursivement l'instruction mo_addcontour(x,y) (n'oubliez pas de le fermer), puis intégrer l'expression du tenseur avec un mo_lineintegral(3).

Remarque : On pensera à définir le contour dans le sens direct pour que la normale soit bien une normale sortante à la surface.
Sélectionner le bloc correspondant à la plaque et utiliser la commande mo_blockintegral(19).
Cette façon de procéder est la plus intéressante car elle permet de calculer une valeur moyennée de la force par la technique dite de la « coquille d'œuf » (eggshell). FEMM va automatiquement choisir une bande d'éléments de l'air entourant le bloc, calculer l'intégrale sur plusieurs contours traversant cette bande, et calculer la moyenne des valeurs ainsi obtenues. Ceci permet de filtrer les éventuelles erreurs d'interpolation pouvant intervenir sur les points d'un unique contour.

➤ Testez les deux méthodes sur votre premier calcul.

➤ À l'aide du théorème d'Ampère, développez un modèle analytique approché permettant de calculer la force, et vérifiez la concordance des ordres de grandeur.

Force en fonction de la position

Une fois que les calculs précédents validés, nous allons tracer la force en fonction de la position de la plaque (entrefer $e$ variable).

Pour cela, faites varier $e$ entre 1 et 20 mm, et calculez la force pour chaque position. Nous calculerons également la coénergie du système afin d'obtenir une troisième méthode de calcul de la force par la dérivation de la coénergie. En effet, dans notre cas, nous avons aussi :

\[F_e = \frac{\partial~\widetilde{W}}{\partial\,e}\]

Où $F_e$ est la valeur de la force dans la direction de la coordonnée généralisée $e$ (dans notre cas : $-{\bf u_y}$).

Conseil d'implantation :

Commencez par l'entrefer le plus grand pour que la boîte infinie soit bien adaptée pour ce cas géométrique.

Bouclez seulement sur la résolution du problème en ayant préalablement déplacé la plaque avec un mi_movetranslate ou mi_movetranslate2. Une bonne astuce consiste à mettre préalablement les lignes et le blocklabel dans le même groupe, et translater le groupe.

Approximez la dérivée de la coénergie par : \[F_y\left(e_k-\frac{\Delta e}{2}\right) = \frac{\widetilde{W}(e_{k+1})-\widetilde{W}(e_{k})}{\Delta e}\] où : $e_{k+1} = e_k -\Delta e$.

➤ Tracez la courbe $|F_y(e)|$ en superposant les valeurs obtenues par les 3 méthodes.

Régime saturé

Maintenant, nous allons nous intéresser au cas plus réaliste où le comportement de chaque matériau ferromagnétique est modélisé par sa courbe B(H).

Comme précédemment, si vous désirez utiliser un matériau dont la caractéristique magnétique est non-linéaire, vous pouvez :

Créer votre matériau avec la commande mi_addmaterial, puis ajouter point par point ceux de la courbe correspondante avec mi_addbhpoint('nom',B,H).
Importer directement un matériau de la librairie avec mi_getmaterial. Par défaut, cette dernière contient beaucoup de matériaux utiles, si celui dont on a besoin s'y trouve, c'est la méthode que je vous conseille.

➤ Tracez la courbe $|F_y(Ic)|$ (pour $e = 1\,\text{mm}$) afin de voir l'influence de la saturation. Pour cela : faites une première boucle sur Ic en linéaire comme dans les questions précédentes, puis refaites les calculs après avoir remplacé vos matériaux magnétiques par les vrais, c'est-à-dire ceux importés depuis la librairie de FEMM.

Conseil d'implantation : Une fois que votre calcul en non-linéaire fonctionne, bouclez seulement sur la résolution précédée d'un mi_modifycircprop ou mi_setcurrent permettant de modifier la valeur du courant de circuit.

Bonus (facultatif)

Reprendre l'étude pour une géométrie cylindrique comme les ventouses de retenue de porte coup-feu du couloir des salles de TP (vous pourrez ainsi mesurer approximativement les différentes tailles du circuit magnétique) :

Ventouse cylindrique

Circuit magnétique cylindrique

Chauffage par induction

But du sujet : Étudier et simuler le fonctionnement d'une plaque à induction.

Notions abordées :

Problème magnétoharmonique ;

Calcul des courants induits ;

Condition d'impédance de frontière ;

Couplage faible avec une résolution thermique.

Ma famille adore les œufs à la coque. Ça tombe bien, nous avons la chance d'avoir une plaque à induction qui nous permet de les faire cuire en 5 minutes chrono (2 min pour faire bouillir l'eau + 3 min de cuisson) :

Ma casserole

Le principe de fonctionnement est simple : sous la plaque de vitrocéramique, une bobine alimentée par un courant sinusoïdal à fréquence assez élevée (typiquement 25 kHz) crée un champ de même fréquence qui induit ainsi des courants de Foucault dans le cul de la casserole (Maxwell-Faraday).

N'ayant pas trop envie de démonter ma propre plaque personnelle, j'ai trouvé une photo de l'intérieur d'une autre :

Crédit photo : By Wdwd - Own work, CC BY-SA 3.0, Link.

La bobine est une bobine circulaire mono-couche (pancake) constituée de fil de Litz. Ce type de fil est particulièrement utile pour les applications à fréquence élevée. Il est constitué de multiples brins de très petits diamètres permettant ainsi de s'affranchir de l'effet de peau dans les inducteurs bobinés avec. Un exemple de fil que nous utilisons au laboratoire pour les manips de transfert inductif est visible ci-dessous :

Fil de Litz

D'un point de vue magnétique, seules deux régions sont dignes d'intérêt ; les autres peuvent être assimilées à de l'air. Les caractéristiques de notre problème sont alors :

Inducteur :

Diamètre intérieur : 2,5 cm
Nombre de spires : 16
Diamètre du fil (toron) : 0,4 cm
Constitution : 50 brins de 0,4 mm de diamètre
Distance au haut de la plaque : 1,5 cm

Casserole (charge) :

Matériau : Acier inoxydable ($\mu_r = 400$, $\sigma = 1,67~\text{MS}\cdot\text{m}^{-1}$)
Épaisseur du fond : 1 cm
Diamètre : 16 cm

Quelques détails théoriques

La formulation du problème à résoudre ressemble à celle utilisée jusqu'alors pour des problèmes statiques, à ceci près que nous prendrons en compte l'équation de Maxwell-Faraday. Le courant source étant sinusoïdal (de pulsation $\omega$ ), nous pourrons utiliser le repère complexe pour nos grandeurs.

Dans FEMM, la transformation associée est : \[ u(t) \mapsto \underline{u} ~ , ~\text{tel que :} ~ ~ u(t) = \operatorname{Re}(\underline{u}\,\exp(i\,\omega\,t)) \] \[ \text{Et ainsi :} ~ ~ \frac{\partial \, u}{\partial t} \mapsto i\,\omega\,\underline{u}\]

Attention : FEMM utilise la convention anglo-saxonne qui repose sur un invariant d'amplitude. En général, la transformation complexe que nous utilisons d'ordinaire repose sur un invariant de puissance. En d'autre termes : habituellement, le module du complexe représente la valeur efficace de la grandeur ; mais dans FEMM c'est sa valeur max.

Il faudra donc être vigilant dans :

la définition du courant du circuit,

les calculs issus de ceux des grandeurs énergétiques.

L'équation générale complexe résolue dans le cadre de la magnétoharmonique est ainsi : \[{\bf rot}\left(\underline{\nu}\,{\bf rot\,\underline{a}}\right) + i\,\omega\,\sigma\,{\bf \underline{a}} = {\bf \underline{j_s}} - \sigma\,{\bf grad}\,\underline{v}\]

Où :

${\bf \underline{j_s}}$ : est la densité de courant source (imposée par le circuit),
$- i\,\omega\,\sigma\,{\bf \underline{a}}$ : est le terme représentant les courants induits,
$- \sigma\,{\bf grad}\,\underline{v}$ : est un terme constant en 2D servant uniquement à assurer la conservation du courant dans les conducteurs, c'est-à-dire : \[ \underline{I_c} = \iint\limits_{\text{section portant I_c}} {\bf \underline{j_{\text{tot}}}}\cdot{\bf d S}\]
\[\text{Avec :} ~ ~ {\bf \underline{j_{\text{tot}}}} = {\bf \underline{j_s}} - i\,\omega\,\sigma\,{\bf \underline{a}} - \sigma\,{\bf grad}\,\underline{v}\]

Ceci dit, allons-y !

Premiers calculs à fréquence modérée

Pour commencer nous choisirons un courant d'alimentation de 10 A efficaces à 1 kHz.

➤ Implantez le problème correspondant en laissant le maillage par défaut créé automatiquement par FEMM.

On n'oubliera pas de définir le matériau de l'inducteur correctement :

MATLAB :
mi_addmaterial('Litz',1,1,0,0,sigmaCu,0,0,1,5,0,0,nbrins,dbrins);
Python :
femm.mi_addmaterial('Litz',1,1,0,0,sigmaCu,0,0,1,5,0,0,nbrins,dbrins)
Et de donner la valeur max du courant dans le circuit.

Vous pouvez alors constater les imprécisions dues au manque de finesse du maillage en traçant la densité de courants induits dans l'Inox.

Dans notre cas, la profondeur de peau $\delta$ dans la charge est de : \[\delta = \sqrt{\frac{2}{\sigma\,\mu\,\omega}} \approx 0,6~\text{mm}\]

➤ Résoudre à nouveau le problème après avoir imposé une taille d'élément dans la charge d'au moins ${\delta}/{3}$.

La densité de puissance dissipée dans l'Inox peut être calculée de deux façons :

Par intégration des Pertes Joule directement (dans le bloc correspondant avec un mo_blockintegral(4)).
À partir de l'énergie magnétique fournie par l'inducteur.
On a déjà vu qu'en linéaire celle-ci peut être calculée par l'intégrale de ${\bf a}\cdot{\bf j}$ dans la bobine. En dérivant cette dernière par rapport au temps, on obtient la puissance délivrée par la bobine. Finalement, en prenant la partie réelle de cette puissance apparente, on obtient la puissance active transmise à la charge par l'inducteur. Après simplification : : \[P_{tr} = -\operatorname{Im}\left[\frac{\omega}{2}\,\left(2\,\pi \iint\limits_{\text{inducteur}} {\bf \underline{a}}\cdot{\bf j^*}\,r\,\text{d}r\,\text{d}z\right)\right] \]

➤ Calculez $P_{tr}$ de ces deux façons et vérifiez qu'on obtient la même valeur.

Problèmes liés à la montée en fréquence

Nous venons de voir qu'il était nécessaire d'adapter le maillage de la pièce en Inox en fonction de l'épaisseur de peau (et donc de la fréquence). Nous avons déjà dû mailler finement le cas précédent à 1 kHZ.

Si nous désirons effectuer des simulations à 25 kHz, l'effet de peau étant 5 fois plus petit, le nombre d'éléments du problème risque d'exploser, ce qui va entraîner un temps de calcul pour mailler et résoudre très important, voir une insuffisance de ressources (personnellement, sous Virt'UL : après avoir péniblement réussi à résoudre, FEMM crashe en beauté lors de l'affichage des résultats).

Heureusement, nous disposons d'une technique pour remédier à cela : une condition aux limites particulière appelée « Impédance de surface » ou « Condition de petit effet de peau » (Small skin depth).

Impédance de surface

Vous avez dû observer que plus la fréquence est élevée, moins le champ pénètre dans la charge. Pour de hautes fréquences, on peut donc retirer le bloc correspondant du domaine d'étude.

Ceci se fait simplement en :

ne créant pas pas de label dans le bloc ;
sélectionnant le segment de bloc situé sur l'axe et en le détruisant avec un mi_deleteselectedsegments. (Attention : faites-le après avoir créé la boîte infinie, donc après le mi_makeABC()s).

Les trois segments de la pièce en inox restants sont désormais des frontières du domaine, nous devons donc leur imposer une condition traduisant notre problème (équivalente à la présence du matériau de l'autre côté). À fréquence élevée, le champ magnétique est nul à l'intérieur de la pièce à chauffer, et la densité de courant est purement surfacique (comme si elle n'existait que sur une épaisseur $\delta$ très petite. Ainsi, en développant le saut de la composante tangentielle de ${\bf h}$ sur les bords du conducteur, on obtient la condition mixte suivante :

\[\frac{\partial\,{\bf \underline{a}}}{\partial n} + \frac{1+i}{\delta}\,{\bf \underline{a}} = 0\]

Dans FEMM, une telle condition se crée facilement avec :

MATLAB :

mi_addboundprop('Impedance_surface',0,0,0,0,mur,sigmaInox,0,0,1,0,0);

Python :

femm.mi_addboundprop('Impedance_surface',0,0,0,0,mur,sigmaInox,0,0,1,0,0)

Il nous reste un dernier petit souci à régler : le calcul de la densité de pertes dans la pièce en Inox. Puisqu'elle n'est plus maillée, on ne peut plus intégrer la densité de perte Joule à l'intérieur. Ce n'est pas gênant, on l'estimera par le calcul de la puissance dans l'inducteur vu ci-avant.

➤ Pour une fréquence de 10 kHz, comparez les résultats obtenus par les deux méthodes :

en maillant l'Inox avec une taille d'élément de $\delta/3$ et en calculant les pertes des deux façons possibles ;
en utilisant la condition d'impédance de surface.

Un exemple de calcul avec impédance de surface est donné ci-dessous :

Lignes de champ à 10 kHz avec impédance de surface

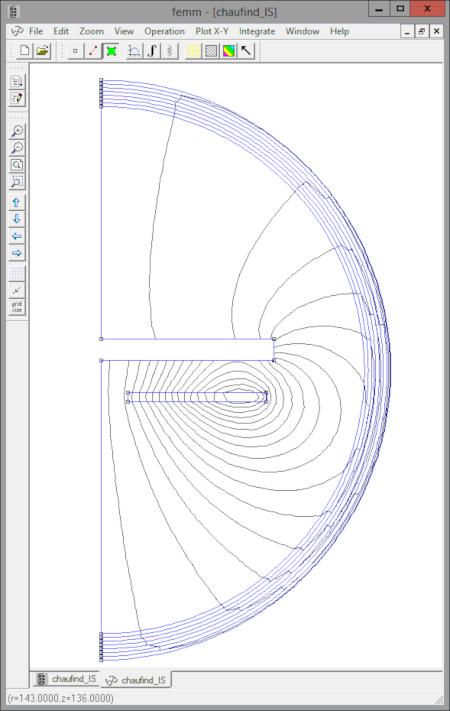
Simulation à 25 kHz et calcul de la température

➤ Forts des résultats précédents, faites une simulation à la vraie fréquence de fonctionnement de la plaque : 25 kHz (avec seulement la condition d'impédance de surface).

➤ Trouvez la valeur du courant inducteur permettant d'atteindre l'ébullition en 2 minutes grâce à un couplage faible avec la thermique.

Cadeau : Pour ce faire, je vous fournis ci-dessous un morceau de programme qui permet de résoudre le problème thermique (en transitoire) avec FEMM. Il est à exécuter après votre résolution magnétique permettant de calculer ce que j'ai appelée Ptr : la puissance transmise par l'inducteur à la casserole.

MATLAB :

% A executer apres la resolution magnetoharmonique
% --> prend en entree : Ptr (= puissance transmise a la casserole)

R = 80;   % inutile si deja defini
ep = 10;  % meme chose
eb = 3;   % epaisseur bord
hc = 100; % hauteur casserole
he = 80;  % hauteur d'eau

Ta = 273+20; % Temperature ambiante
h = 10;      % coeff. convection naturelle avec air

newdocument(2);  % nouveau pbm thermique
hi_probdef('millimeters','axi')

hi_getmaterial('Water');   % eau
hi_modifymaterial('Water',0,'Eau');
hi_getmaterial('347 Stainless Steel');  % inox
hi_modifymaterial('347 Stainless Steel',0,'Inox');

hi_addboundprop('Convection',2, 0, 0, Ta, h, 0);
hi_addconductorprop('P_transmise', 0, Ptr, 0);
hi_addconductorprop('Temp_ini', Ta, 0, 1);

hi_drawpolygon([0,0;R,0;R,ep;R,ep+hc;R-eb,ep+hc;R-eb,ep+he;R-eb,ep;0,ep]);
hi_addnode(0,ep+he);
hi_addsegment(0,ep,0,ep+he);
hi_addsegment(0,ep+he,R-eb,ep+he);
hi_zoomnatural;

hi_addblocklabel(R/2,ep/2);
hi_selectlabel(R/2,ep/2);
hi_setblockprop('Inox', 1, 0, 1);
hi_clearselected;
hi_addblocklabel(R/2,ep+he/2);
hi_selectlabel(R/2,ep+he/2);
hi_setblockprop('Eau', 1, 0, 1);
hi_clearselected;

hi_selectsegment(R/2,0);
hi_setsegmentprop('<none>', 0, 1, 0, 1, 'Temp_ini'); % 1er calcul pour init
hi_clearselected;
hi_selectsegment(R,ep/2);
hi_selectsegment(R,ep+hc/2);
hi_selectsegment(R-eb/2,R-(hc-he)/2);
hi_selectsegment(R/2,ep+he);
hi_setsegmentprop('Convection', 0, 1, 0, 1, '<none>' );
hi_clearselected;

% 1ere resolution pour fixer T = Ta partout
hi_saveas('Temp0.feh');
hi_analyze();

% puissance transmise par l'inducteur
hi_selectsegment(R/2,0);
hi_setsegmentprop('<none>', 0, 1, 0, 1,'P_transmise');

% boucle pour regime transitoire
deltaT = 4; % pas de temps en secondes
npas = 30;  % nombre de pas
t = 0:deltaT:npas*deltaT; % temps
Tmoy = zeros(1,npas+1);   % initialisation
Tmoy(1) = Ta; 
for n=1:npas
    nomfichier = char("Temp"+(n-1)+".anh");
    hi_probdef('millimeters','axi',1.e-8,1,30,nomfichier,deltaT);
    hi_saveas(char("Temp"+n+".feh"));
    hi_analyze();
    hi_loadsolution();
	% recuperation de la temperature moyenne sur le fond interieur
    ho_addcontour(0,ep);
    ho_addcontour(R-eb,ep);
    res = ho_lineintegral(3);
    Tmoy(n+1) = res(1);
    ho_close();
end
plot(t,Tmoy,'linewidth',2));
xlabel("Temps (en s)");
ylabel("Temperature moyenne du fond (en K)");
title("Evolution de la temperature dans la casserole")
grid on

Python :

# A executer apres la resolution magnetoharmonique
# --> prend en entree : Ptr (= puissance transmise a la casserole)
import matplotlib.pyplot as plt

R = 80   # inutile si deja defini
ep = 10  # meme chose
eb = 3   # epaisseur bord
hc = 100 # hauteur casserole
he = 80  # hauteur d'eau

Ta = 273+20 # Temperature ambiante
h = 10      # coeff. convection naturelle avec air

femm.newdocument(2)  # nouveau pbm thermique
femm.hi_probdef('millimeters','axi',1e-8)

femm.hi_getmaterial('Water')   # eau
femm.hi_modifymaterial('Water',0,'Eau')
femm.hi_getmaterial('347 Stainless Steel')  # inox
femm.hi_modifymaterial('347 Stainless Steel',0,'Inox')

femm.hi_addboundprop('Convection',2, 0, 0, Ta, h, 0)
femm.hi_addconductorprop('P_transmise', 0, Ptr, 0)
femm.hi_addconductorprop('Temp_ini', Ta, 0, 1)

femm.hi_drawline(0,0,R,0)
femm.hi_drawline(R,0,R,ep)
femm.hi_drawline(R,ep,R,ep+hc)
femm.hi_drawline(R,ep+hc,R-eb,ep+hc)
femm.hi_drawline(R-eb,ep+hc,R-eb,ep+he)
femm.hi_drawline(R-eb,ep+he,R-eb,ep)
femm.hi_drawline(R-eb,ep,0,ep)
femm.hi_drawline(0,ep,0,0)
femm.hi_addnode(0,ep+he)
femm.hi_addsegment(0,ep,0,ep+he)
femm.hi_addsegment(0,ep+he,R-eb,ep+he)
femm.hi_zoomnatural()

femm.hi_addblocklabel(R/2,ep/2)
femm.hi_selectlabel(R/2,ep/2)
femm.hi_setblockprop('Inox', 1, 0, 1)
femm.hi_clearselected()
femm.hi_addblocklabel(R/2,ep+he/2)
femm.hi_selectlabel(R/2,ep+he/2)
femm.hi_setblockprop('Eau', 1, 0, 1)
femm.hi_clearselected()

femm.hi_selectsegment(R/2,0)
femm.hi_setsegmentprop('<none>', 0, 1, 0, 1, 'Temp_ini') # 1er calcul pour init
femm.hi_clearselected()
femm.hi_selectsegment(R,ep/2)
femm.hi_selectsegment(R,ep+hc/2)
femm.hi_selectsegment(R-eb/2,R-(hc-he)/2)
femm.hi_selectsegment(R/2,ep+he)
femm.hi_setsegmentprop('Convection', 0, 1, 0, 1, '<none>' )
femm.hi_clearselected()

# 1ere resolution pour fixer T = Ta partout
femm.hi_saveas('Temp0.FEH')
femm.hi_analyze()

# puissance transmise par l'inducteur
femm.hi_selectsegment(R/2,0)
femm.hi_setsegmentprop('<none>', 0, 1, 0, 1,'P_transmise')

# boucle pour regime transitoire
deltaT = 4 # pas de temps en secondes
npas = 30  # nombre de pas
t = np.linspace(0,npas*deltaT,npas+1) # temps
Tmoy = np.zeros(npas+1)   # initialisation
Tmoy[0] = Ta
for n in range(npas):
    nomfichier = "Temp{}.anh".format(n)
    femm.hi_probdef('millimeters','axi',1.e-8,1,30,nomfichier,deltaT)
    femm.hi_saveas("Temp{}.feh".format(n+1))
    femm.hi_analyze()
    femm.hi_loadsolution()
    # recuperation de la temperature moyenne sur le fond interieur
    femm.ho_addcontour(0,ep)
    femm.ho_addcontour(R-eb,ep)
    res = femm.ho_lineintegral(3)
    Tmoy[n+1] = res[0]
    femm.ho_close()

plt.plot(t,Tmoy,'b',lw=2)
plt.title('Évolution de la température dans la casserole')
plt.xlabel('Temps (en s)')
plt.ylabel('Température moyenne du fond (en K)')
plt.grid()
plt.show()

Remarque : Initialement, FEMM ne permettait de résoudre que des problèmes thermiques stationnaires. Depuis quelque temps, a été introduit un moyen permettant de résoudre le régime transitoire en chargeant une résolution précédente et un pas de temps dans la définition du problème. C'est ce qui est fait ci-dessus dans la boucle.

Vous pouvez modifier la phase d'exploitation du programme à votre guise. Par exemple, j'ai exporté le tracé de la température à chaque pas de temps pour faire une petite animation :

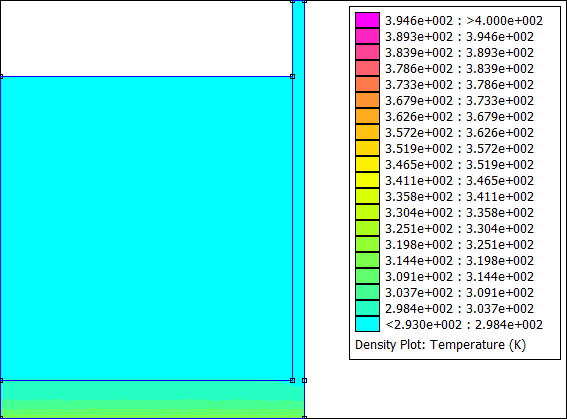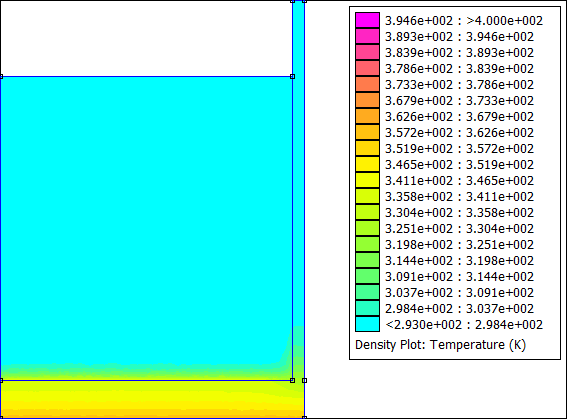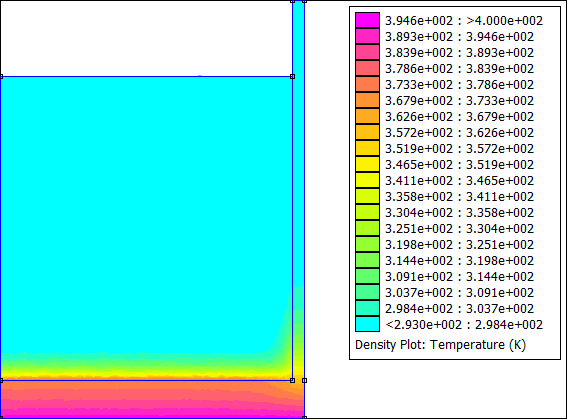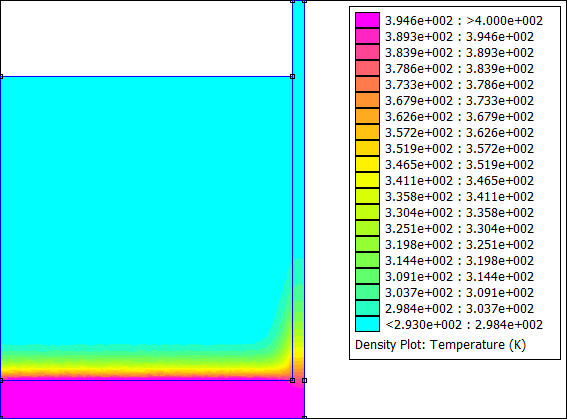
Temperature

Machine Synchrone à Aimants Permanents (MSAP)

But du sujet : Étudier et simuler le fonctionnement d'une machine électrique classique : une MSAP.

Notions abordées :

Conditions de périodicité ;

Bande de roulement;

Calcul de couple.

Pour cette dernière application, nous allons nous intéresser à une machine électrique. Ce que vous allez voir pourra vous être très utile si vous choisissez l'année prochaine le bloc de compétence S9-BC14 « Machines Électriques », ou si vous vous orientez vers un des nombreux stages de fin d'études en conception de machines électriques.

Préambule

Description

La machine étudiée est une machine synchrone triphasée à aimants permanents à 3 paires de pôles (lisses, aimants posés en surface avec aimantation radiale), 2 encoches par pôle et par phase, alimentée à 50 hz. Compte-tenu des symétries, on peut limiter le domaine d'étude à un pôle. Une représentation schématique est donnée ci-dessous :

1 pôle de la MASAP

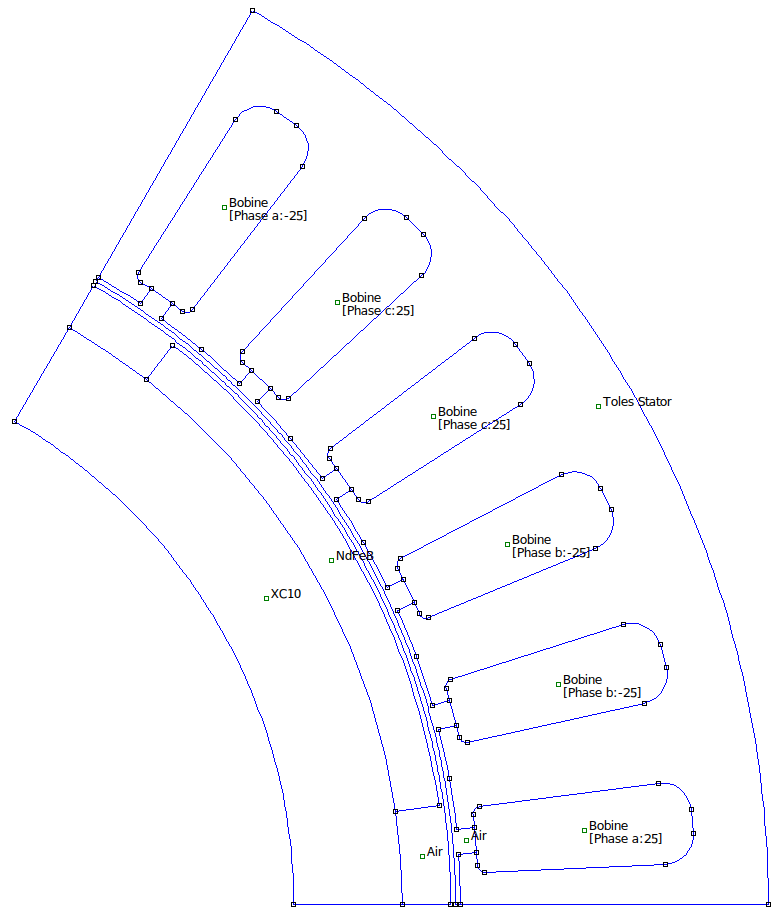
Remarque importante :

En réduisant ainsi le domaine, on gagne en simplicité et en complexité : moins d'éléments, taille du système matriciel réduite, donc moins d'occupation mémoire (RAM) et moins de temps de calcul (CPU). Il faudra juste veiller à :

bien prendre en compte la périodicité dans les calculs post-opération (couple, énergies, flux),

bien définir les conditions aux limites.

Conditions aux limites

Pour notre problème, ces conditions aux frontières seront :

des conditions de Dirichlet homogènes sur les bords des culasses rotoriques et statoriques pour forcer le champ à rester dans la machine : on les appelle souvent « conditions de fond de culasse ».
des conditions d'antipériodicité sur le bas et le haut du domaine, traduisant le fait que sur les pôles voisins de celui étudié, le problème est l'exact opposé. On les applique sur des lignes maillées de la même façon, et elles se traduisent par : \[ a_z\,(\text{noeud}\,i){\LARGE |}_{\text{ligne}\,2} = -a_z\,(\text{noeud}\,i){\LARGE |}_{\text{ligne}\,1} \]

Bande de roulement

On ajoute également une bande de roulement dans l'entrefer. Dans la plupart des logiciels « experts », on trouve des techniques permettant de prendre en compte la rotation de l'intérieur de la machine tout en conservant le maillage du rotor et du stator : ce sont des bandes ou surfaces de roulement / glissement.

Dans FEMM, la bande roulement s'appuie sur une condition d'antipériodicité particulière reliant une fine zone de l'entrefer liée au rotor avec une autre liée au stator, la bande centrale restant non maillée. Vous trouverez de plus amples détails sur son implantation sur la page dédiée du Wiki.

Une figure représentant celle utilisée sur notre machine est donnée ci-dessous :

Bande de roulement

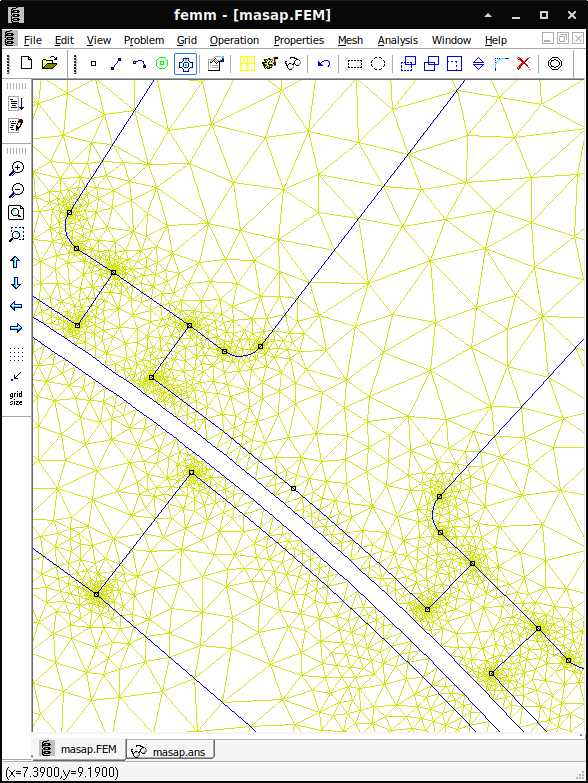
Inplantation (cadeau)

Afin de vous évitez l'étape un peu fastidieuse de définition de la géométrie, je vous donne ci-dessous un exemple de programme définissant entièrement le problème et permettant de calculer la distribution de champ à vide (sans courant d'alimentation).

MATLAB :

close all 
clear 
clc
addpath('C:\femm42\mfiles')

% Donnees probleme (toutes les longueurs sont en cm)
p = 3;                  % nombre de paires de poles
Lz = 20;                % longueur
Ra = 10;                % rayon d'alesage
alphae = 0.5;           % larg. ang. encoche
alphai = 0.2;           % larg. ang. isthme
he = 3;                 % hauteur encoche
hi = 0.25;              % hauteur isthme
ecs = 1;                % epaisseur culasse stator
e = 0.2;                % entrefer
ea = 0.6;               % epaisseur aimant
ecr = 1.5;              % epaisseur culasse rotor
alphaa = (9-alphai)/12; % coef. arc polaire

taup = pi/p;   % pas polaire
taud = taup/6; % pas dentaire

N = 25;        % nombre de spires
Ieff = 0;      % valeur eff courant d'alim.
w = 2*pi*50;   % pulsation

Ia = 0;
Ib = 0;
Ic = 0;

Omega = w/p; % vitesse
angRot = 0;  % position rotor : 0 (plus simple a reperer car position geometrie)
angStat = 0; % on laisse 0 : centre sur phase a

openfemm()
newdocument(0)
mi_probdef(0,'centimeters','planar',1e-8,Lz); 

% Materiaux
mi_getmaterial('Air');
mi_getmaterial('M-19 Steel');
mi_modifymaterial('M-19 Steel',0,'Toles Stator');
mi_getmaterial('1010 Steel')
mi_modifymaterial('1010 Steel',0,'XC10');
mi_getmaterial('Copper');
mi_modifymaterial('Copper',0,'Bobine');
mi_getmaterial('N30');
mi_modifymaterial('N30',0,'NdFeB');

% Sources
mi_addcircprop('Phase a',Ia,1);
mi_addcircprop('Phase b',Ib,1);
mi_addcircprop('Phase c',Ic,1);

% CL
mi_addboundprop('Fond culasse',0,0,0,0);

mi_addboundprop('antiper1',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper2',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper3',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper4',0,0,0,0,0,0,0,0,5,0,0);

mi_addboundprop('Bande Roulement',0,0,0,0,0,0,0,0,7,angRot,angStat);
 % Attention : bug dans mi_addboundprop.m, on doit rajouter :   
mi_modifyboundprop('Bande Roulement',10,angRot); 

% stator
R1 = Ra+hi;
R2 = R1+he;
R3 = R2+ecs;
theta1 = (1-alphai)*taud/2;
theta2 = (1-alphae)*taud/2;
theta3 = (1+alphae)*taud/2;
theta4 = (1+alphai)*taud/2;
mi_addnode(Ra,0);
mi_drawarc(Ra,0,Ra*cos(theta1),Ra*sin(theta1),theta1*180/pi,1);
mi_drawpolyline([Ra*cos(theta1),Ra*sin(theta1); ... 
    R1*cos(theta1),R1*sin(theta1); R1*cos(theta2),R1*sin(theta2); ...
    R2*cos(theta2),R2*sin(theta2)]);
mi_drawarc(R2*cos(theta2),R2*sin(theta2),R2*cos(theta3),R2*sin(theta3), ...
    alphae*taud*180/pi,5);
mi_drawpolyline([R2*cos(theta3),R2*sin(theta3); ... 
    R1*cos(theta3),R1*sin(theta3); R1*cos(theta4),R1*sin(theta4); ...
    Ra*cos(theta4),Ra*sin(theta4)]);
mi_drawarc(Ra*cos(theta4),Ra*sin(theta4),Ra*cos(taud),Ra*sin(taud), .... 
    theta1*180/pi,1);
r1 = 0.1;
mi_createradius(R1*cos(theta2),R1*sin(theta2),r1);
mi_createradius(R1*cos(theta3),R1*sin(theta3),r1);
r2 = 0.4;
mi_createradius(R2*cos(theta2),R2*sin(theta2),r2);
mi_createradius(R2*cos(theta3),R2*sin(theta3),r2);
mi_addsegment(R1*cos(theta1),R1*sin(theta1),R1*cos(theta4),R1*sin(theta4));
mi_selectgroup(0);
mi_copyrotate(0, 0, taud*180/pi, 5 );
mi_drawline(Ra,0,R3,0);
mi_drawline(Ra*cos(taup),Ra*sin(taup), R3*cos(taup),R3*sin(taup));
mi_drawarc(R3,0,R3*cos(taup),R3*sin(taup),taup*180/pi,5);
mi_drawline(Ra,0,Ra-e/3,0);
mi_drawline(Ra*cos(taup),Ra*sin(taup),(Ra-e/3)*cos(taup),(Ra-e/3)*sin(taup));
mi_drawarc((Ra-e/3),0,(Ra-e/3)*cos(taup),(Ra-e/3)*sin(taup),taup*180/pi,1);

mi_addblocklabel((Ra+R1)/2*cos(taud/2),(Ra+R1)/2*sin(taud/2));
mi_selectlabel((Ra+R1)/2*cos(taud/2),(Ra+R1)/2*sin(taud/2));
mi_setblockprop('Air',1,0,0,0,0,0);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud/2),(R2+R1)/2*sin(taud/2));
mi_selectlabel((R2+R1)/2*cos(taud/2),(R2+R1)/2*sin(taud/2));
mi_setblockprop('Bobine',1,0,'Phase a',0,2,N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*1.5),(R2+R1)/2*sin(taud*1.5));
mi_addblocklabel((R2+R1)/2*cos(taud*2.5),(R2+R1)/2*sin(taud*2.5));
mi_selectlabel((R2+R1)/2*cos(taud*1.5),(R2+R1)/2*sin(taud*1.5));
mi_selectlabel((R2+R1)/2*cos(taud*2.5),(R2+R1)/2*sin(taud*2.5));
mi_setblockprop('Bobine',1,0,'Phase c',0,3,-N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*3.5),(R2+R1)/2*sin(taud*3.5));
mi_addblocklabel((R2+R1)/2*cos(taud*4.5),(R2+R1)/2*sin(taud*4.5));
mi_selectlabel((R2+R1)/2*cos(taud*3.5),(R2+R1)/2*sin(taud*3.5));
mi_selectlabel((R2+R1)/2*cos(taud*4.5),(R2+R1)/2*sin(taud*4.5));
mi_setblockprop('Bobine',1,0,'Phase b',0,4,N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*5.5),(R2+R1)/2*sin(taud*5.5));
mi_selectlabel((R2+R1)/2*cos(taud*5.5),(R2+R1)/2*sin(taud*5.5));
mi_setblockprop('Bobine',1,0,'Phase a',0,2,-N);
mi_clearselected;
mi_addblocklabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_selectlabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_setblockprop('Toles Stator',1,0,0,0,1,0);
mi_clearselected;
mi_selectsegment(R2,0);
mi_selectsegment(R2*cos(taup),R2*sin(taup));
mi_setsegmentprop('antiper1',0,1,0,1);
mi_clearselected;
mi_selectsegment((Ra-e/6),0);
mi_selectsegment((Ra-e/6)*cos(taup),(Ra-e/6)*sin(taup));
mi_setsegmentprop('antiper2',0,1,0,1);
mi_clearselected;
mi_selectarcsegment(R3*cos(taup/2),R3*sin(taup/2));
mi_setarcsegmentprop(5,'Fond culasse',0,1); 
mi_clearselected;

% rotor
R1 = Ra-2*e/3;
R2 = Ra-e;
R3 = R2-ea;
R4 = R3-ecr;
theta1 = (1-alphaa)*taup/2;
theta2 = (1+alphaa)*taup/2;
mi_drawpolyline([R4,0;R3,0;R1,0]);
mi_drawpolyline([R4*cos(taup),R4*sin(taup);R3*cos(taup),R3*sin(taup); ...
    R1*cos(taup),R1*sin(taup)]);
mi_drawline(R3*cos(theta1),R3*sin(theta1),R2*cos(theta1),R2*sin(theta1));
mi_drawline(R3*cos(theta2),R3*sin(theta2),R2*cos(theta2),R2*sin(theta2));
mi_addarc(R4,0,R4*cos(taup),R4*sin(taup),taup*180/pi,5);
mi_addarc(R3,0,R3*cos(theta1),R3*sin(theta1),theta1*180/pi,5);
mi_addarc(R3*cos(theta2),R3*sin(theta2),R3*cos(taup),R3*sin(taup), ... 
    theta1*180/pi,5);
mi_addarc(R3*cos(theta1),R3*sin(theta1),R3*cos(theta2),R3*sin(theta2), ...
    alphaa*taup*180/pi,5);
mi_addarc(R2*cos(theta1),R2*sin(theta1),R2*cos(theta2),R2*sin(theta2), ... 
    alphaa*taup*180/pi,1);
mi_addarc(R1,0,R1*cos(taup),R1*sin(taup),taup*180/pi,1);

mi_addblocklabel((R2+R3)/2*cos(theta1/2),(R2+R3)/2*sin(theta1/2));
mi_selectlabel((R2+R3)/2*cos(theta1/2),(R2+R3)/2*sin(theta1/2));
mi_setblockprop('Air',1,0,0,0,5,0);
mi_clearselected;
mi_addblocklabel((R4+R3)/2*cos(taup/2),(R4+R3)/2*sin(taup/2));
mi_selectlabel((R4+R3)/2*cos(taup/2),(R4+R3)/2*sin(taup/2));
mi_setblockprop('XC10',1,0,0,0,6,0);
mi_clearselected;
mi_addblocklabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_selectlabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_setblockprop('NdFeB',1,0,0,'theta',6,0);
mi_clearselected;
mi_selectsegment(R2,0);
mi_selectsegment(R2*cos(taup),R2*sin(taup));
mi_setsegmentprop('antiper3',0,1,0,5);
mi_clearselected;
mi_selectsegment((R4+R3)/2,0);
mi_selectsegment((R4+R3)/2*cos(taup),(R4+R3)/2*sin(taup));
mi_setsegmentprop('antiper4',0,1,0,5);
mi_clearselected;
mi_selectarcsegment(R4*cos(taup/2),R4*sin(taup/2));
mi_setarcsegmentprop(5,'Fond culasse',0,1); 
mi_clearselected;

mi_selectarcsegment((Ra-2*e/3)*cos(taup/2),(Ra-2*e/3)*sin(taup/2));
mi_selectarcsegment((Ra-e/3)*cos(taup/2),(Ra-e/3)*sin(taup/2));
mi_setarcsegmentprop(1,'Bande Roulement',0,1);
mi_clearselected;

mi_zoomnatural;
mi_saveas('masap.FEM')

ntheta = 30;  % nombre de positions
dtheta_rad = pi/p/ntheta;
dtheta_deg = dtheta_rad*180/pi;  % FEMM travaille en degres...
for n = 1:ntheta
   mi_analyse();
   mi_loadsolution();
   mo_hidepoints;
   mo_showdensityplot(0,0,2,0,'mag');
   mo_savebitmap(char("imagesMag\B"+n+".bmp"));
   mi_modifyboundprop('Bande Roulement',10,angRot+n*dtheta_deg);
end
mi_modifyboundprop('Bande Roulement',10,angRot); % retour position initiale

Python :

import numpy as np
import femm

# Donnees probleme (toutes les longueurs sont en cm)
pp = 3                  # nombre de paires de poles
Lz = 20                 # longueur
Ra = 10                 # rayon d'alesage
alphae = 0.5            # larg. ang. encoche
alphai = 0.2            # larg. ang. isthme
he = 3                  # hauteur encoche
hi = 0.25               # hauteur isthme
ecs = 1                 # epaisseur culasse stator
e = 0.2                 # entrefer
ea = 0.6                # epaisseur aimant
ecr = 1.5               # epaisseur culasse rotor
alphaa = (9-alphai)/12; # coef. arc polaire

taup = np.pi/p   # pas polaire
taud = taup/6 # pas dentaire

N = 25        # nombre de spires
Ieff = 0      # valeur eff courant d'alim.
w = 2*np.pi*50   # pulsation

Ia = 0
Ib = 0
Ic = 0

Omega = w/p  # vitesse
angRot = 0   # position rotor : 0 (plus simple a reperer car position geometrie)
angStat = 0  # on laisse 0 : centre sur phase a

femm.openfemm()
femm.newdocument(0)
femm.mi_probdef(0,'centimeters','planar',1e-8,Lz) 

# Materiaux
femm.mi_getmaterial('Air')
femm.mi_getmaterial('M-19 Steel')
femm.mi_modifymaterial('M-19 Steel',0,'Toles Stator')
femm.mi_getmaterial('1010 Steel')
femm.mi_modifymaterial('1010 Steel',0,'XC10')
femm.mi_getmaterial('Copper')
femm.mi_modifymaterial('Copper',0,'Bobine')
femm.mi_getmaterial('N30')
femm.mi_modifymaterial('N30',0,'NdFeB')

# Sources
femm.mi_addcircprop('Phase a',Ia,1)
femm.mi_addcircprop('Phase b',Ib,1)
femm.mi_addcircprop('Phase c',Ic,1)

# CL
femm.mi_addboundprop('Fond culasse',0,0,0,0)

femm.mi_addboundprop('antiper1',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper2',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper3',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper4',0,0,0,0,0,0,0,0,5,0,0)

femm.mi_addboundprop('Bande Roulement',0,0,0,0,0,0,0,0,7,angRot,angStat)
 # Attention : bug dans femm.mi_addboundprop.m, on doit rajouter :   
femm.mi_modifyboundprop('Bande Roulement',10,angRot) 

# stator
R1 = Ra+hi
R2 = R1+he
R3 = R2+ecs
theta1 = (1-alphai)*taud/2
theta2 = (1-alphae)*taud/2
theta3 = (1+alphae)*taud/2
theta4 = (1+alphai)*taud/2
femm.mi_addnode(Ra,0)
femm.mi_drawarc(Ra,0,Ra*np.cos(theta1),Ra*np.sin(theta1),theta1*180/np.pi,1)
femm.mi_drawline(Ra*np.cos(theta1),Ra*np.sin(theta1),R1*np.cos(theta1),R1*np.sin(theta1))
femm.mi_drawline(R1*np.cos(theta1),R1*np.sin(theta1),R1*np.cos(theta2),R1*np.sin(theta2))
femm.mi_drawline(R1*np.cos(theta2),R1*np.sin(theta2),R2*np.cos(theta2),R2*np.sin(theta2))
femm.mi_drawarc(R2*np.cos(theta2),R2*np.sin(theta2),R2*np.cos(theta3),R2*np.sin(theta3),
           alphae*taud*180/np.pi,5)
femm.mi_drawline(R2*np.cos(theta3),R2*np.sin(theta3),R1*np.cos(theta3),R1*np.sin(theta3))
femm.mi_drawline(R1*np.cos(theta3),R1*np.sin(theta3),R1*np.cos(theta4),R1*np.sin(theta4))
femm.mi_drawline(R1*np.cos(theta4),R1*np.sin(theta4),Ra*np.cos(theta4),Ra*np.sin(theta4))

femm.mi_drawarc(Ra*np.cos(theta4),Ra*np.sin(theta4),Ra*np.cos(taud),Ra*np.sin(taud),
           theta1*180/np.pi,1)
r1 = 0.1
femm.mi_createradius(R1*np.cos(theta2),R1*np.sin(theta2),r1)
femm.mi_createradius(R1*np.cos(theta3),R1*np.sin(theta3),r1)
r2 = 0.4
femm.mi_createradius(R2*np.cos(theta2),R2*np.sin(theta2),r2)
femm.mi_createradius(R2*np.cos(theta3),R2*np.sin(theta3),r2)
femm.mi_addsegment(R1*np.cos(theta1),R1*np.sin(theta1),R1*np.cos(theta4),R1*np.sin(theta4))
femm.mi_selectgroup(0)
femm.mi_copyrotate(0, 0, taud*180/np.pi, 5 )
femm.mi_drawline(Ra,0,R3,0)
femm.mi_drawline(Ra*np.cos(taup),Ra*np.sin(taup), R3*np.cos(taup),R3*np.sin(taup))
femm.mi_drawarc(R3,0,R3*np.cos(taup),R3*np.sin(taup),taup*180/np.pi,5)
femm.mi_drawline(Ra,0,Ra-e/3,0)
femm.mi_drawline(Ra*np.cos(taup),Ra*np.sin(taup),(Ra-e/3)*np.cos(taup),(Ra-e/3)*np.sin(taup))
femm.mi_drawarc((Ra-e/3),0,(Ra-e/3)*np.cos(taup),(Ra-e/3)*np.sin(taup),taup*180/np.pi,1)

femm.mi_addblocklabel((Ra+R1)/2*np.cos(taud/2),(Ra+R1)/2*np.sin(taud/2))
femm.mi_selectlabel((Ra+R1)/2*np.cos(taud/2),(Ra+R1)/2*np.sin(taud/2))
femm.mi_setblockprop('Air',1,0,0,0,0,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud/2),(R2+R1)/2*np.sin(taud/2))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud/2),(R2+R1)/2*np.sin(taud/2))
femm.mi_setblockprop('Bobine',1,0,'Phase a',0,2,N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*1.5),(R2+R1)/2*np.sin(taud*1.5))
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*2.5),(R2+R1)/2*np.sin(taud*2.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*1.5),(R2+R1)/2*np.sin(taud*1.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*2.5),(R2+R1)/2*np.sin(taud*2.5))
femm.mi_setblockprop('Bobine',1,0,'Phase c',0,3,-N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*3.5),(R2+R1)/2*np.sin(taud*3.5))
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*4.5),(R2+R1)/2*np.sin(taud*4.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*3.5),(R2+R1)/2*np.sin(taud*3.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*4.5),(R2+R1)/2*np.sin(taud*4.5))
femm.mi_setblockprop('Bobine',1,0,'Phase b',0,4,N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*5.5),(R2+R1)/2*np.sin(taud*5.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*5.5),(R2+R1)/2*np.sin(taud*5.5))
femm.mi_setblockprop('Bobine',1,0,'Phase a',0,2,-N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('Toles Stator',1,0,0,0,1,0)
femm.mi_clearselected()
femm.mi_selectsegment(R2,0)
femm.mi_selectsegment(R2*np.cos(taup),R2*np.sin(taup))
femm.mi_setsegmentprop('antiper1',0,1,0,1)
femm.mi_clearselected()
femm.mi_selectsegment((Ra-e/6),0)
femm.mi_selectsegment((Ra-e/6)*np.cos(taup),(Ra-e/6)*np.sin(taup))
femm.mi_setsegmentprop('antiper2',0,1,0,1)
femm.mi_clearselected()
femm.mi_selectarcsegment(R3*np.cos(taup/2),R3*np.sin(taup/2))
femm.mi_setarcsegmentprop(5,'Fond culasse',0,1) 
femm.mi_clearselected()

# rotor
R1 = Ra-2*e/3
R2 = Ra-e
R3 = R2-ea
R4 = R3-ecr
theta1 = (1-alphaa)*taup/2
theta2 = (1+alphaa)*taup/2
femm.mi_drawline(R4,0,R3,0)
femm.mi_drawline(R3,0,R1,0)
femm.mi_drawline(R4*np.cos(taup),R4*np.sin(taup),R3*np.cos(taup),R3*np.sin(taup))
femm.mi_drawline(R3*np.cos(taup),R3*np.sin(taup),R1*np.cos(taup),R1*np.sin(taup))
femm.mi_drawline(R3*np.cos(theta1),R3*np.sin(theta1),R2*np.cos(theta1),R2*np.sin(theta1))
femm.mi_drawline(R3*np.cos(theta2),R3*np.sin(theta2),R2*np.cos(theta2),R2*np.sin(theta2))
femm.mi_addarc(R4,0,R4*np.cos(taup),R4*np.sin(taup),taup*180/np.pi,5)
femm.mi_addarc(R3,0,R3*np.cos(theta1),R3*np.sin(theta1),theta1*180/np.pi,5)
femm.mi_addarc(R3*np.cos(theta2),R3*np.sin(theta2),R3*np.cos(taup),R3*np.sin(taup),
               theta1*180/np.pi,5)
femm.mi_addarc(R3*np.cos(theta1),R3*np.sin(theta1),R3*np.cos(theta2),R3*np.sin(theta2),
               alphaa*taup*180/np.pi,5)
femm.mi_addarc(R2*np.cos(theta1),R2*np.sin(theta1),R2*np.cos(theta2),R2*np.sin(theta2),
               alphaa*taup*180/np.pi,1)
femm.mi_addarc(R1,0,R1*np.cos(taup),R1*np.sin(taup),taup*180/np.pi,1)

femm.mi_addblocklabel((R2+R3)/2*np.cos(theta1/2),(R2+R3)/2*np.sin(theta1/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(theta1/2),(R2+R3)/2*np.sin(theta1/2))
femm.mi_setblockprop('Air',1,0,0,0,5,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R4+R3)/2*np.cos(taup/2),(R4+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R4+R3)/2*np.cos(taup/2),(R4+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('XC10',1,0,0,0,6,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('NdFeB',1,0,0,'theta',6,0)
femm.mi_clearselected()
femm.mi_selectsegment(R2,0)
femm.mi_selectsegment(R2*np.cos(taup),R2*np.sin(taup))
femm.mi_setsegmentprop('antiper3',0,1,0,5)
femm.mi_clearselected()
femm.mi_selectsegment((R4+R3)/2,0)
femm.mi_selectsegment((R4+R3)/2*np.cos(taup),(R4+R3)/2*np.sin(taup))
femm.mi_setsegmentprop('antiper4',0,1,0,5)
femm.mi_clearselected()
femm.mi_selectarcsegment(R4*np.cos(taup/2),R4*np.sin(taup/2))
femm.mi_setarcsegmentprop(5,'Fond culasse',0,1) 
femm.mi_clearselected()

femm.mi_selectarcsegment((Ra-2*e/3)*np.cos(taup/2),(Ra-2*e/3)*np.sin(taup/2))
femm.mi_selectarcsegment((Ra-e/3)*np.cos(taup/2),(Ra-e/3)*np.sin(taup/2))
femm.mi_setarcsegmentprop(1,'Bande Roulement',0,1)
femm.mi_clearselected()

femm.mi_zoomnatural()
femm.mi_saveas('masap.FEM')

ntheta = 30                # nombre de positions
dtheta_rad = np.pi/p/ntheta
dtheta_deg = dtheta_rad*180/np.pi  # FEMM travaile en degres...
for n in range(ntheta):
    femm.mi_analyze()
    femm.mi_loadsolution()
    femm.mo_hidepoints()
    femm.mo_showdensityplot(0,0,2,0,'mag')
    femm.mo_savebitmap("imagesMag{}.bmp".format(n+1))
    femm.mi_modifyboundprop('Bande Roulement',10,angRot+n*dtheta_deg)
# Retour position initiale_
femm.mi_modifyboundprop('Bande Roulement',10,angRot)

Avec les résultats obtenus, on peut réaliser la petite animation suivante :

Flux à vide

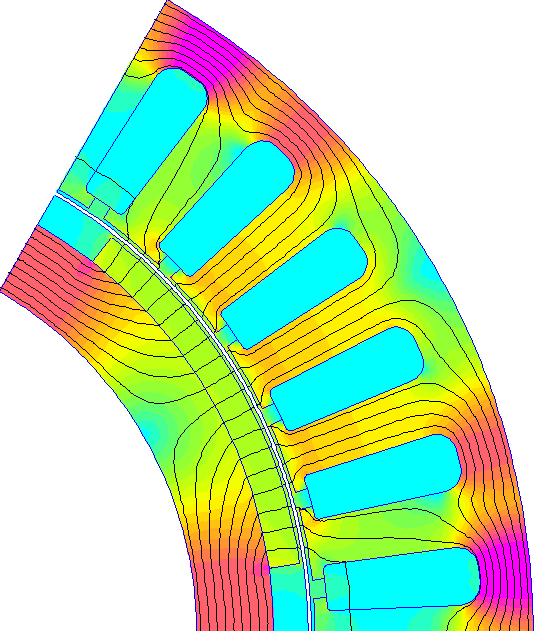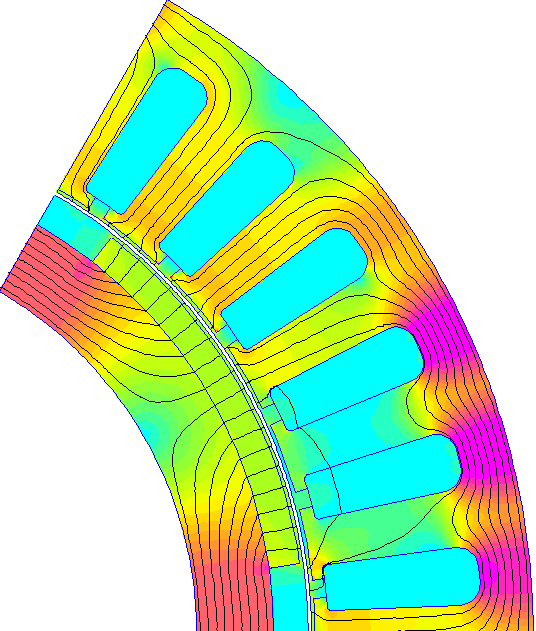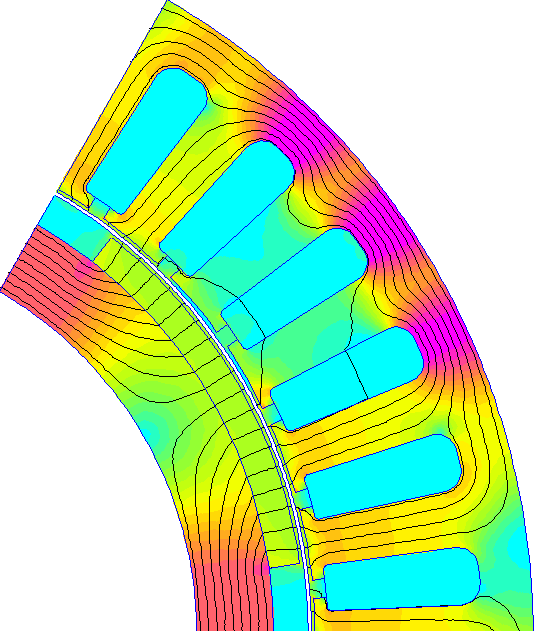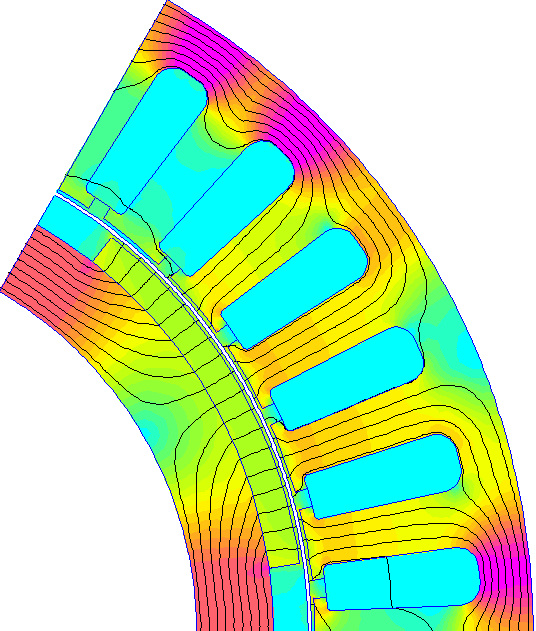
➤ Analysez le programme fourni et commentez les différentes parties.

Exploitation

Modèle externe : Flux, fem, et estimation du couple

➤ Modifiez le programme précédent pour calculer les flux à vide

Astuce : Pour calculer les flux, regardez la commande mo_getcircuitproperties.

➤ Intégrer les courbes obtenues pour en déduire les fem (forces électromotrices) à vide :

Formes d'onde du flux et fem à vide

➤ Déterminez l'angle de calage $\psi$ de la machine permettant d'avoir des courants d'alimentation en phase avec les fem (fonctionnement à couple max) dans le cas d'une alimentation sinusoïdale classique de la forme :

$$\left\{\begin{aligned}I_a(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi\right)\\I_b(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi-\frac{2\pi}{3}\right)\\I_c(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi+\frac{2\pi}{3}\right)\end{aligned}\right.$$

➤ Tracez alors l'allure de l'estimation du couple issue des fem à vide en fonction de la position du rotor :

On rappelle la formule : $$\Gamma_{\text{em}} = \frac{1}{\Omega} \sum_{k = (a,b,c)} E_k \cdot I_k$$

Exemple de résultat :

Estimation du couple

Calcul du couple par éléments finis

Le calcul du couple exercé sur le rotor se fait de la même façon que celui de la force vu pour la ventouse :

Par le tenseur de Maxwell moyenné : basé sur la technique de la « coquille d'œuf » vue précédemment.

La densité surfacique de force est issue du tenseur des contraintes électromagnétiques de Maxwell, on utilise comme surface $S$ un cylindre passant dans l'entrefer, et on obtient pour le moment du couple : \[ \Gamma = \iint_{S}\,\left( {\bf r} \wedge \left(\overline{\overline{{\bf T}}}\cdot{\bf n}\right) \right) \cdot {\bf u_z} \, \text{d} S\] Pour notre problème 2D, on peut considérer un arc de cercle $C$ passant dans l'entrefer, pour obtenir : \[\Gamma = 2\,p\,L_z\,\int_{C}\,\left( {\bf r} \wedge\overline{\overline{{\bf T}}}\cdot{\bf n}\right) \cdot {\bf u_z} \, \text{d}l\] Une expression moyennée dans une couche d'éléments dans l'air entourant le rotor peut-être directement calculée par FEMM.
On sélectionne les blocs correspondants à la culasse rotorique et l'aimant (groupe 6 dans le programme fourni), et on applique mo_blockintegral(22) pour avoir le terme intégral.
Par une méthode des travaux virtuels (avec dérivée de la coénergie) :
Vous avez vu dans le premier EC du bloc et en cours de Machines Électrique que le couple était la dérivée de la coénergie par rapport à la position angulaire à courant constant : \[\Gamma = \left.\frac{\partial\,\widetilde{W}}{\partial \theta}\right|_{I\,\text{constant}}\] On calcule donc la coénergie dans tout le pôle de la machine pour 2 positions : $\theta_k$ et $\theta_k+\Delta\theta$, à courant constant. Puis, on obtient le couple par : \[ \Gamma \left(\theta_k\right) = 2\,p\,\frac{\widetilde{W}(\theta_k+\Delta \theta)-\widetilde{W}(\theta_k)}{\Delta\theta}\]

➤ En utilisant une alimentation identique au modèle externe ci-dessus, calculez puis tracez le couple en fonction de la position du rotor, en superposant les courbes correspondant aux deux méthodes :

Calcul du couple

➤ Commentez les allures des deux courbes de couple (par le modèle externe et par la MEF).

Félicitations !

Si vous avez tout assimilé et tout compris vous êtes devenu un bon utilisateur de FEMM. Avec de la pratique, vous pourrez même devenir un power user !

Références

D. Meeker, Finite Element Method Magnetics: HomePage, site internet de FEMM, https://www.femm.info.
D. Meeker, Finite Element Method Magnetics, User’s Manual, Version 4.2, 16 mai 2020
D. Meeker, Finite Element Method Magnetics: OctaveFEMM, User’s Manual, 17 mars 2018.
D. Meeker, Finite Element Method Magnetics: pyFEMM 0.1.3, User’s Manual, 20 juillet 2021.

Crédits

Tout le contenu de ce site (y compris les images) a été créé par l'auteur et est placé sous licence creative commons CC BY-SA 4.0.

Ressources

Seuls des logiciels libres ont été utilisés pour élaborer ce mini-site, en particulier :

mdBook : pour la génération du site à partir de simples fichiers Markdown.
Xfig : pour la création des schémas.
GIMP : pour la retouche d'images et la création de gifs animés.

Webpoly TP FEMM - ENSEM Énergie 2A