Chauffage par induction

But du sujet : Étudier et simuler le fonctionnement d'une plaque à induction.

Notions abordées :

• Problème magnétoharmonique ;
• Calcul des courants induits ;
• Condition d'impédance de frontière ;
• Couplage faible avec une résolution thermique.

Ma famille adore les œufs à la coque. Ça tombe bien, nous avons la chance d'avoir une plaque à induction qui nous permet de les faire cuire en 5 minutes chrono (2 min pour faire bouillir l'eau + 3 min de cuisson) :

Le principe de fonctionnement est simple : sous la plaque de vitrocéramique, une bobine alimentée par un courant sinusoïdal à fréquence assez élevée (typiquement 25 kHz) crée un champ de même fréquence qui induit ainsi des courants de Foucault dans le cul de la casserole (Maxwell-Faraday).

N'ayant pas trop envie de démonter ma propre plaque personnelle, j'ai trouvé une photo de l'intérieur d'une autre :

La bobine est une bobine circulaire mono-couche (pancake) constituée de fil de Litz. Ce type de fil est particulièrement utile pour les applications à fréquence élevée. Il est constitué de multiples brins de très petits diamètres permettant ainsi de s'affranchir de l'effet de peau dans les inducteurs bobinés avec. Un exemple de fil que nous utilisons au laboratoire pour les manips de transfert inductif est visible ci-dessous :

D'un point de vue magnétique, seules deux régions sont dignes d'intérêt ; les autres peuvent être assimilées à de l'air. Les caractéristiques de notre problème sont alors :

1. Inducteur :

• Diamètre intérieur : 2,5 cm
• Nombre de spires : 16
• Diamètre du fil (toron) : 0,4 cm
• Constitution : 50 brins de 0,4 mm de diamètre
• Distance au haut de la plaque : 1,5 cm

2. Casserole (charge) :

• Matériau : Acier inoxydable (\(\mu_r = 400\), \(\sigma = 1,67~\text{MS}\cdot\text{m}^{-1}\))
• Épaisseur du fond : 1 cm
• Diamètre : 16 cm

Quelques détails théoriques

La formulation du problème à résoudre ressemble à celle utilisée jusqu'alors pour des problèmes statiques, à ceci près que nous prendrons en compte l'équation de Maxwell-Faraday. Le courant source étant sinusoïdal (de pulsation \(\omega\) ), nous pourrons utiliser le repère complexe pour nos grandeurs.

Dans FEMM, la transformation associée est : \[ u(t) \mapsto \underline{u} ~ , ~\text{tel que :} ~ ~ u(t) = \operatorname{Re}(\underline{u}\,\exp(i\,\omega\,t)) \] \[ \text{Et ainsi :} ~ ~ \frac{\partial \, u}{\partial t} \mapsto i\,\omega\,\underline{u}\]

Attention : FEMM utilise la convention anglo-saxonne qui repose sur un invariant d'amplitude. En général, la transformation complexe que nous utilisons d'ordinaire repose sur un invariant de puissance. En d'autre termes : habituellement, le module du complexe représente la valeur efficace de la grandeur ; mais dans FEMM c'est sa valeur max.

Il faudra donc être vigilant dans :

1. la définition du courant du circuit,
2. les calculs issus de ceux des grandeurs énergétiques.

L'équation générale complexe résolue dans le cadre de la magnétoharmonique est ainsi : \[{\bf rot}\left(\underline{\nu}\,{\bf rot\,\underline{a}}\right) + i\,\omega\,\sigma\,{\bf \underline{a}} = {\bf \underline{j_s}} - \sigma\,{\bf grad}\,\underline{v}\]

Où :

• \({\bf \underline{j_s}}\) : est la densité de courant source (imposée par le circuit),
• \(- i\,\omega\,\sigma\,{\bf \underline{a}}\) : est le terme représentant les courants induits,
• \(- \sigma\,{\bf grad}\,\underline{v}\) : est un terme constant en 2D servant uniquement à assurer la conservation du courant dans les conducteurs, c'est-à-dire : \[ \underline{I_c} = \iint\limits_{\text{section portant I_c}} {\bf \underline{j_{\text{tot}}}}\cdot{\bf d S}\]
  \[\text{Avec :} ~ ~ {\bf \underline{j_{\text{tot}}}} = {\bf \underline{j_s}} - i\,\omega\,\sigma\,{\bf \underline{a}} - \sigma\,{\bf grad}\,\underline{v}\]

Ceci dit, allons-y !

Premiers calculs à fréquence modérée

Pour commencer nous choisirons un courant d'alimentation de 10 A efficaces à 1 kHz.

➤ Implantez le problème correspondant en laissant le maillage par défaut créé automatiquement par FEMM.

On n'oubliera pas de définir le matériau de l'inducteur correctement :

• MATLAB :

mi_addmaterial('Litz',1,1,0,0,sigmaCu,0,0,1,5,0,0,nbrins,dbrins);

• Python :

femm.mi_addmaterial('Litz',1,1,0,0,sigmaCu,0,0,1,5,0,0,nbrins,dbrins)

Et de donner la valeur max du courant dans le circuit.

Vous pouvez alors constater les imprécisions dues au manque de finesse du maillage en traçant la densité de courants induits dans l'Inox.

Dans notre cas, la profondeur de peau \(\delta\) dans la charge est de : \[\delta = \sqrt{\frac{2}{\sigma\,\mu\,\omega}} \approx 0,6~\text{mm}\]

➤ Résoudre à nouveau le problème après avoir imposé une taille d'élément dans la charge d'au moins \({\delta}/{3}\).

La densité de puissance dissipée dans l'Inox peut être calculée de deux façons :

1. Par intégration des Pertes Joule directement (dans le bloc correspondant avec un mo_blockintegral(4)).
2. À partir de l'énergie magnétique fournie par l'inducteur.
   On a déjà vu qu'en linéaire celle-ci peut être calculée par l'intégrale de \({\bf a}\cdot{\bf j}\) dans la bobine. En dérivant cette dernière par rapport au temps, on obtient la puissance délivrée par la bobine. Finalement, en prenant la partie réelle de cette puissance apparente, on obtient la puissance active transmise à la charge par l'inducteur. Après simplification : : \[P_{tr} = -\operatorname{Im}\left[\frac{\omega}{2}\,\left(2\,\pi \iint\limits_{\text{inducteur}} {\bf \underline{a}}\cdot{\bf j^*}\,r\,\text{d}r\,\text{d}z\right)\right] \]

➤ Calculez \(P_{tr}\) de ces deux façons et vérifiez qu'on obtient la même valeur.

Problèmes liés à la montée en fréquence

Nous venons de voir qu'il était nécessaire d'adapter le maillage de la pièce en Inox en fonction de l'épaisseur de peau (et donc de la fréquence). Nous avons déjà dû mailler finement le cas précédent à 1 kHZ.

Si nous désirons effectuer des simulations à 25 kHz, l'effet de peau étant 5 fois plus petit, le nombre d'éléments du problème risque d'exploser, ce qui va entraîner un temps de calcul pour mailler et résoudre très important, voir une insuffisance de ressources (personnellement, sous Virt'UL : après avoir péniblement réussi à résoudre, FEMM crashe en beauté lors de l'affichage des résultats).

Heureusement, nous disposons d'une technique pour remédier à cela : une condition aux limites particulière appelée « Impédance de surface » ou « Condition de petit effet de peau » (Small skin depth).

Impédance de surface

Vous avez dû observer que plus la fréquence est élevée, moins le champ pénètre dans la charge. Pour de hautes fréquences, on peut donc retirer le bloc correspondant du domaine d'étude.

Ceci se fait simplement en :

1. ne créant pas pas de label dans le bloc ;
2. sélectionnant le segment de bloc situé sur l'axe et en le détruisant avec un mi_deleteselectedsegments. (Attention : faites-le après avoir créé la boîte infinie, donc après le mi_makeABC()s).

Les trois segments de la pièce en inox restants sont désormais des frontières du domaine, nous devons donc leur imposer une condition traduisant notre problème (équivalente à la présence du matériau de l'autre côté). À fréquence élevée, le champ magnétique est nul à l'intérieur de la pièce à chauffer, et la densité de courant est purement surfacique (comme si elle n'existait que sur une épaisseur \(\delta\) très petite. Ainsi, en développant le saut de la composante tangentielle de \({\bf h}\) sur les bords du conducteur, on obtient la condition mixte suivante :

\[\frac{\partial\,{\bf \underline{a}}}{\partial n} + \frac{1+i}{\delta}\,{\bf \underline{a}} = 0\]

Dans FEMM, une telle condition se crée facilement avec :

• MATLAB :

mi_addboundprop('Impedance_surface',0,0,0,0,mur,sigmaInox,0,0,1,0,0);

• Python :

femm.mi_addboundprop('Impedance_surface',0,0,0,0,mur,sigmaInox,0,0,1,0,0)

Il nous reste un dernier petit souci à régler : le calcul de la densité de pertes dans la pièce en Inox. Puisqu'elle n'est plus maillée, on ne peut plus intégrer la densité de perte Joule à l'intérieur. Ce n'est pas gênant, on l'estimera par le calcul de la puissance dans l'inducteur vu ci-avant.

➤ Pour une fréquence de 10 kHz, comparez les résultats obtenus par les deux méthodes :

• en maillant l'Inox avec une taille d'élément de \(\delta/3\) et en calculant les pertes des deux façons possibles ;
• en utilisant la condition d'impédance de surface.

Un exemple de calcul avec impédance de surface est donné ci-dessous :

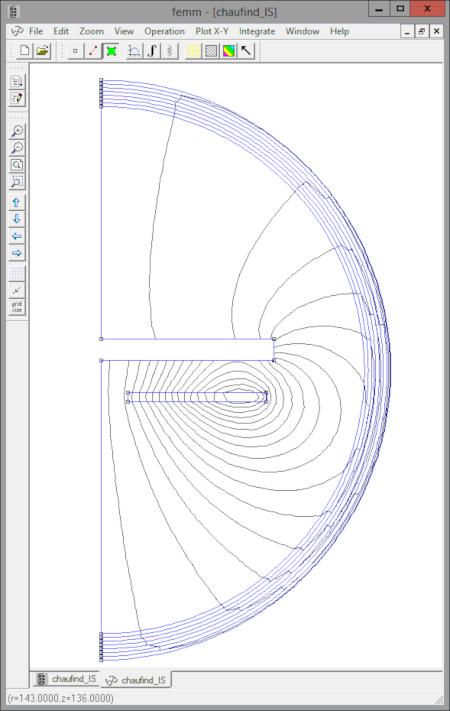
Simulation à 25 kHz et calcul de la température

➤ Forts des résultats précédents, faites une simulation à la vraie fréquence de fonctionnement de la plaque : 25 kHz (avec seulement la condition d'impédance de surface).

➤ Trouvez la valeur du courant inducteur permettant d'atteindre l'ébullition en 2 minutes grâce à un couplage faible avec la thermique.

Cadeau : Pour ce faire, je vous fournis ci-dessous un morceau de programme qui permet de résoudre le problème thermique (en transitoire) avec FEMM. Il est à exécuter après votre résolution magnétique permettant de calculer ce que j'ai appelée Ptr : la puissance transmise par l'inducteur à la casserole.

• MATLAB :

% A executer apres la resolution magnetoharmonique
% --> prend en entree : Ptr (= puissance transmise a la casserole)

R = 80;   % inutile si deja defini
ep = 10;  % meme chose
eb = 3;   % epaisseur bord
hc = 100; % hauteur casserole
he = 80;  % hauteur d'eau

Ta = 273+20; % Temperature ambiante
h = 10;      % coeff. convection naturelle avec air

newdocument(2);  % nouveau pbm thermique
hi_probdef('millimeters','axi')

hi_getmaterial('Water');   % eau
hi_modifymaterial('Water',0,'Eau');
hi_getmaterial('347 Stainless Steel');  % inox
hi_modifymaterial('347 Stainless Steel',0,'Inox');

hi_addboundprop('Convection',2, 0, 0, Ta, h, 0);
hi_addconductorprop('P_transmise', 0, Ptr, 0);
hi_addconductorprop('Temp_ini', Ta, 0, 1);

hi_drawpolygon([0,0;R,0;R,ep;R,ep+hc;R-eb,ep+hc;R-eb,ep+he;R-eb,ep;0,ep]);
hi_addnode(0,ep+he);
hi_addsegment(0,ep,0,ep+he);
hi_addsegment(0,ep+he,R-eb,ep+he);
hi_zoomnatural;

hi_addblocklabel(R/2,ep/2);
hi_selectlabel(R/2,ep/2);
hi_setblockprop('Inox', 1, 0, 1);
hi_clearselected;
hi_addblocklabel(R/2,ep+he/2);
hi_selectlabel(R/2,ep+he/2);
hi_setblockprop('Eau', 1, 0, 1);
hi_clearselected;

hi_selectsegment(R/2,0);
hi_setsegmentprop('<none>', 0, 1, 0, 1, 'Temp_ini'); % 1er calcul pour init
hi_clearselected;
hi_selectsegment(R,ep/2);
hi_selectsegment(R,ep+hc/2);
hi_selectsegment(R-eb/2,R-(hc-he)/2);
hi_selectsegment(R/2,ep+he);
hi_setsegmentprop('Convection', 0, 1, 0, 1, '<none>' );
hi_clearselected;

% 1ere resolution pour fixer T = Ta partout
hi_saveas('Temp0.feh');
hi_analyze();

% puissance transmise par l'inducteur
hi_selectsegment(R/2,0);
hi_setsegmentprop('<none>', 0, 1, 0, 1,'P_transmise');

% boucle pour regime transitoire
deltaT = 4; % pas de temps en secondes
npas = 30;  % nombre de pas
t = 0:deltaT:npas*deltaT; % temps
Tmoy = zeros(1,npas+1);   % initialisation
Tmoy(1) = Ta; 
for n=1:npas
    nomfichier = char("Temp"+(n-1)+".anh");
    hi_probdef('millimeters','axi',1.e-8,1,30,nomfichier,deltaT);
    hi_saveas(char("Temp"+n+".feh"));
    hi_analyze();
    hi_loadsolution();
	% recuperation de la temperature moyenne sur le fond interieur
    ho_addcontour(0,ep);
    ho_addcontour(R-eb,ep);
    res = ho_lineintegral(3);
    Tmoy(n+1) = res(1);
    ho_close();
end
plot(t,Tmoy,'linewidth',2));
xlabel("Temps (en s)");
ylabel("Temperature moyenne du fond (en K)");
title("Evolution de la temperature dans la casserole")
grid on

• Python :

# A executer apres la resolution magnetoharmonique
# --> prend en entree : Ptr (= puissance transmise a la casserole)
import matplotlib.pyplot as plt

R = 80   # inutile si deja defini
ep = 10  # meme chose
eb = 3   # epaisseur bord
hc = 100 # hauteur casserole
he = 80  # hauteur d'eau

Ta = 273+20 # Temperature ambiante
h = 10      # coeff. convection naturelle avec air

femm.newdocument(2)  # nouveau pbm thermique
femm.hi_probdef('millimeters','axi',1e-8)

femm.hi_getmaterial('Water')   # eau
femm.hi_modifymaterial('Water',0,'Eau')
femm.hi_getmaterial('347 Stainless Steel')  # inox
femm.hi_modifymaterial('347 Stainless Steel',0,'Inox')

femm.hi_addboundprop('Convection',2, 0, 0, Ta, h, 0)
femm.hi_addconductorprop('P_transmise', 0, Ptr, 0)
femm.hi_addconductorprop('Temp_ini', Ta, 0, 1)

femm.hi_drawline(0,0,R,0)
femm.hi_drawline(R,0,R,ep)
femm.hi_drawline(R,ep,R,ep+hc)
femm.hi_drawline(R,ep+hc,R-eb,ep+hc)
femm.hi_drawline(R-eb,ep+hc,R-eb,ep+he)
femm.hi_drawline(R-eb,ep+he,R-eb,ep)
femm.hi_drawline(R-eb,ep,0,ep)
femm.hi_drawline(0,ep,0,0)
femm.hi_addnode(0,ep+he)
femm.hi_addsegment(0,ep,0,ep+he)
femm.hi_addsegment(0,ep+he,R-eb,ep+he)
femm.hi_zoomnatural()

femm.hi_addblocklabel(R/2,ep/2)
femm.hi_selectlabel(R/2,ep/2)
femm.hi_setblockprop('Inox', 1, 0, 1)
femm.hi_clearselected()
femm.hi_addblocklabel(R/2,ep+he/2)
femm.hi_selectlabel(R/2,ep+he/2)
femm.hi_setblockprop('Eau', 1, 0, 1)
femm.hi_clearselected()

femm.hi_selectsegment(R/2,0)
femm.hi_setsegmentprop('<none>', 0, 1, 0, 1, 'Temp_ini') # 1er calcul pour init
femm.hi_clearselected()
femm.hi_selectsegment(R,ep/2)
femm.hi_selectsegment(R,ep+hc/2)
femm.hi_selectsegment(R-eb/2,R-(hc-he)/2)
femm.hi_selectsegment(R/2,ep+he)
femm.hi_setsegmentprop('Convection', 0, 1, 0, 1, '<none>' )
femm.hi_clearselected()

# 1ere resolution pour fixer T = Ta partout
femm.hi_saveas('Temp0.FEH')
femm.hi_analyze()

# puissance transmise par l'inducteur
femm.hi_selectsegment(R/2,0)
femm.hi_setsegmentprop('<none>', 0, 1, 0, 1,'P_transmise')

# boucle pour regime transitoire
deltaT = 4 # pas de temps en secondes
npas = 30  # nombre de pas
t = np.linspace(0,npas*deltaT,npas+1) # temps
Tmoy = np.zeros(npas+1)   # initialisation
Tmoy[0] = Ta
for n in range(npas):
    nomfichier = "Temp{}.anh".format(n)
    femm.hi_probdef('millimeters','axi',1.e-8,1,30,nomfichier,deltaT)
    femm.hi_saveas("Temp{}.feh".format(n+1))
    femm.hi_analyze()
    femm.hi_loadsolution()
    # recuperation de la temperature moyenne sur le fond interieur
    femm.ho_addcontour(0,ep)
    femm.ho_addcontour(R-eb,ep)
    res = femm.ho_lineintegral(3)
    Tmoy[n+1] = res[0]
    femm.ho_close()

plt.plot(t,Tmoy,'b',lw=2)
plt.title('Évolution de la température dans la casserole')
plt.xlabel('Temps (en s)')
plt.ylabel('Température moyenne du fond (en K)')
plt.grid()
plt.show()

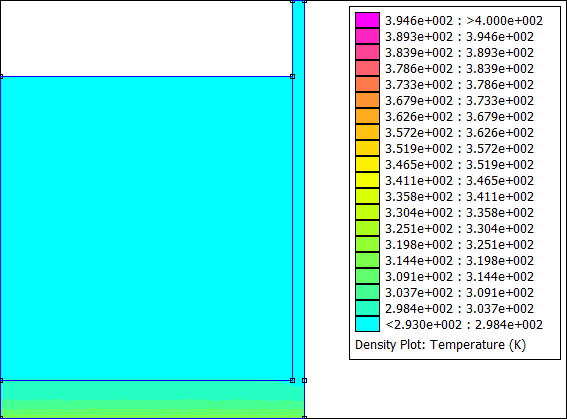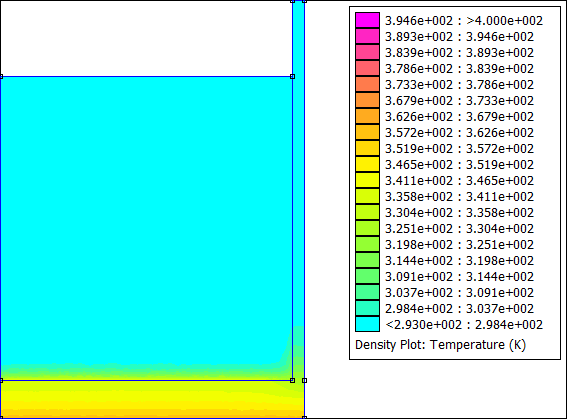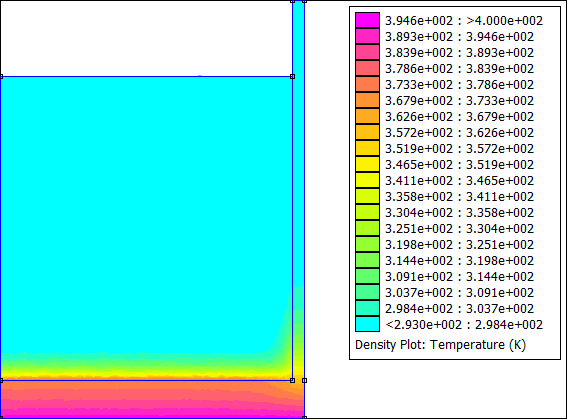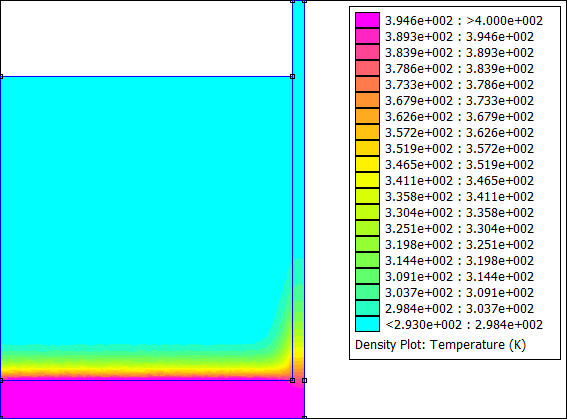
Remarque : Initialement, FEMM ne permettait de résoudre que des problèmes thermiques stationnaires. Depuis quelque temps, a été introduit un moyen permettant de résoudre le régime transitoire en chargeant une résolution précédente et un pas de temps dans la définition du problème. C'est ce qui est fait ci-dessus dans la boucle.

Vous pouvez modifier la phase d'exploitation du programme à votre guise. Par exemple, j'ai exporté le tracé de la température à chaque pas de temps pour faire une petite animation :