Machine Synchrone à Aimants Permanents (MSAP)
But du sujet : Étudier et simuler le fonctionnement d'une machine électrique classique : une MSAP.
Notions abordées :
- Conditions de périodicité ;
- Bande de roulement;
- Calcul de couple.
Pour cette dernière application, nous allons nous intéresser à une machine électrique. Ce que vous allez voir pourra vous être très utile si vous choisissez l'année prochaine le bloc de compétence S9-BC14 « Machines Électriques », ou si vous vous orientez vers un des nombreux stages de fin d'études en conception de machines électriques.
Préambule
Description
La machine étudiée est une machine synchrone triphasée à aimants permanents à 3 paires de pôles (lisses, aimants posés en surface avec aimantation radiale), 2 encoches par pôle et par phase, alimentée à 50 hz. Compte-tenu des symétries, on peut limiter le domaine d'étude à un pôle. Une représentation schématique est donnée ci-dessous :
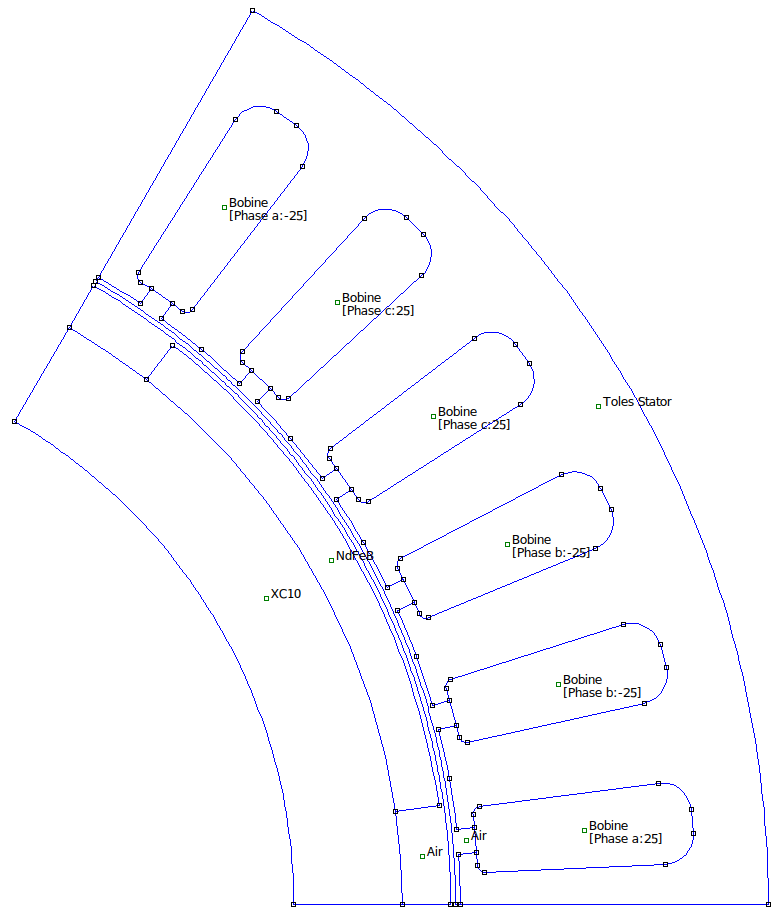
Remarque importante :
En réduisant ainsi le domaine, on gagne en simplicité et en complexité : moins d'éléments, taille du système matriciel réduite, donc moins d'occupation mémoire (RAM) et moins de temps de calcul (CPU). Il faudra juste veiller à :
- bien prendre en compte la périodicité dans les calculs post-opération (couple, énergies, flux),
- bien définir les conditions aux limites.
Conditions aux limites
Pour notre problème, ces conditions aux frontières seront :
-
des conditions de Dirichlet homogènes sur les bords des culasses rotoriques et statoriques pour forcer le champ à rester dans la machine : on les appelle souvent « conditions de fond de culasse ».
-
des conditions d'antipériodicité sur le bas et le haut du domaine, traduisant le fait que sur les pôles voisins de celui étudié, le problème est l'exact opposé. On les applique sur des lignes maillées de la même façon, et elles se traduisent par : \[ a_z\,(\text{noeud}\,i){\LARGE |}_{\text{ligne}\,2} = -a_z\,(\text{noeud}\,i){\LARGE |}_{\text{ligne}\,1} \]
Bande de roulement
On ajoute également une bande de roulement dans l'entrefer. Dans la plupart des logiciels « experts », on trouve des techniques permettant de prendre en compte la rotation de l'intérieur de la machine tout en conservant le maillage du rotor et du stator : ce sont des bandes ou surfaces de roulement / glissement.
Dans FEMM, la bande roulement s'appuie sur une condition d'antipériodicité particulière reliant une fine zone de l'entrefer liée au rotor avec une autre liée au stator, la bande centrale restant non maillée. Vous trouverez de plus amples détails sur son implantation sur la page dédiée du Wiki.
Une figure représentant celle utilisée sur notre machine est donnée ci-dessous :
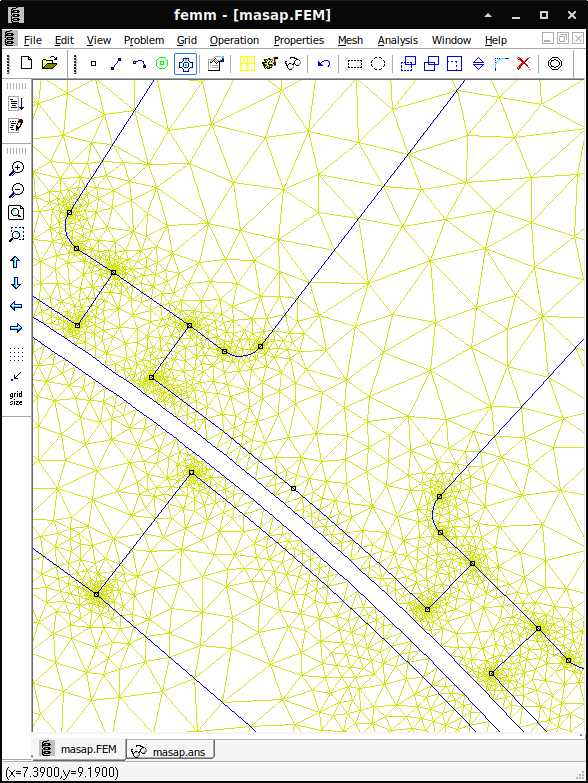
Inplantation (cadeau)
Afin de vous évitez l'étape un peu fastidieuse de définition de la géométrie, je vous donne ci-dessous un exemple de programme définissant entièrement le problème et permettant de calculer la distribution de champ à vide (sans courant d'alimentation).
- MATLAB :
close all
clear
clc
addpath('C:\femm42\mfiles')
% Donnees probleme (toutes les longueurs sont en cm)
p = 3; % nombre de paires de poles
Lz = 20; % longueur
Ra = 10; % rayon d'alesage
alphae = 0.5; % larg. ang. encoche
alphai = 0.2; % larg. ang. isthme
he = 3; % hauteur encoche
hi = 0.25; % hauteur isthme
ecs = 1; % epaisseur culasse stator
e = 0.2; % entrefer
ea = 0.6; % epaisseur aimant
ecr = 1.5; % epaisseur culasse rotor
alphaa = (9-alphai)/12; % coef. arc polaire
taup = pi/p; % pas polaire
taud = taup/6; % pas dentaire
N = 25; % nombre de spires
Ieff = 0; % valeur eff courant d'alim.
w = 2*pi*50; % pulsation
Ia = 0;
Ib = 0;
Ic = 0;
Omega = w/p; % vitesse
angRot = 0; % position rotor : 0 (plus simple a reperer car position geometrie)
angStat = 0; % on laisse 0 : centre sur phase a
openfemm()
newdocument(0)
mi_probdef(0,'centimeters','planar',1e-8,Lz);
% Materiaux
mi_getmaterial('Air');
mi_getmaterial('M-19 Steel');
mi_modifymaterial('M-19 Steel',0,'Toles Stator');
mi_getmaterial('1010 Steel')
mi_modifymaterial('1010 Steel',0,'XC10');
mi_getmaterial('Copper');
mi_modifymaterial('Copper',0,'Bobine');
mi_getmaterial('N30');
mi_modifymaterial('N30',0,'NdFeB');
% Sources
mi_addcircprop('Phase a',Ia,1);
mi_addcircprop('Phase b',Ib,1);
mi_addcircprop('Phase c',Ic,1);
% CL
mi_addboundprop('Fond culasse',0,0,0,0);
mi_addboundprop('antiper1',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper2',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper3',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('antiper4',0,0,0,0,0,0,0,0,5,0,0);
mi_addboundprop('Bande Roulement',0,0,0,0,0,0,0,0,7,angRot,angStat);
% Attention : bug dans mi_addboundprop.m, on doit rajouter :
mi_modifyboundprop('Bande Roulement',10,angRot);
% stator
R1 = Ra+hi;
R2 = R1+he;
R3 = R2+ecs;
theta1 = (1-alphai)*taud/2;
theta2 = (1-alphae)*taud/2;
theta3 = (1+alphae)*taud/2;
theta4 = (1+alphai)*taud/2;
mi_addnode(Ra,0);
mi_drawarc(Ra,0,Ra*cos(theta1),Ra*sin(theta1),theta1*180/pi,1);
mi_drawpolyline([Ra*cos(theta1),Ra*sin(theta1); ...
R1*cos(theta1),R1*sin(theta1); R1*cos(theta2),R1*sin(theta2); ...
R2*cos(theta2),R2*sin(theta2)]);
mi_drawarc(R2*cos(theta2),R2*sin(theta2),R2*cos(theta3),R2*sin(theta3), ...
alphae*taud*180/pi,5);
mi_drawpolyline([R2*cos(theta3),R2*sin(theta3); ...
R1*cos(theta3),R1*sin(theta3); R1*cos(theta4),R1*sin(theta4); ...
Ra*cos(theta4),Ra*sin(theta4)]);
mi_drawarc(Ra*cos(theta4),Ra*sin(theta4),Ra*cos(taud),Ra*sin(taud), ....
theta1*180/pi,1);
r1 = 0.1;
mi_createradius(R1*cos(theta2),R1*sin(theta2),r1);
mi_createradius(R1*cos(theta3),R1*sin(theta3),r1);
r2 = 0.4;
mi_createradius(R2*cos(theta2),R2*sin(theta2),r2);
mi_createradius(R2*cos(theta3),R2*sin(theta3),r2);
mi_addsegment(R1*cos(theta1),R1*sin(theta1),R1*cos(theta4),R1*sin(theta4));
mi_selectgroup(0);
mi_copyrotate(0, 0, taud*180/pi, 5 );
mi_drawline(Ra,0,R3,0);
mi_drawline(Ra*cos(taup),Ra*sin(taup), R3*cos(taup),R3*sin(taup));
mi_drawarc(R3,0,R3*cos(taup),R3*sin(taup),taup*180/pi,5);
mi_drawline(Ra,0,Ra-e/3,0);
mi_drawline(Ra*cos(taup),Ra*sin(taup),(Ra-e/3)*cos(taup),(Ra-e/3)*sin(taup));
mi_drawarc((Ra-e/3),0,(Ra-e/3)*cos(taup),(Ra-e/3)*sin(taup),taup*180/pi,1);
mi_addblocklabel((Ra+R1)/2*cos(taud/2),(Ra+R1)/2*sin(taud/2));
mi_selectlabel((Ra+R1)/2*cos(taud/2),(Ra+R1)/2*sin(taud/2));
mi_setblockprop('Air',1,0,0,0,0,0);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud/2),(R2+R1)/2*sin(taud/2));
mi_selectlabel((R2+R1)/2*cos(taud/2),(R2+R1)/2*sin(taud/2));
mi_setblockprop('Bobine',1,0,'Phase a',0,2,N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*1.5),(R2+R1)/2*sin(taud*1.5));
mi_addblocklabel((R2+R1)/2*cos(taud*2.5),(R2+R1)/2*sin(taud*2.5));
mi_selectlabel((R2+R1)/2*cos(taud*1.5),(R2+R1)/2*sin(taud*1.5));
mi_selectlabel((R2+R1)/2*cos(taud*2.5),(R2+R1)/2*sin(taud*2.5));
mi_setblockprop('Bobine',1,0,'Phase c',0,3,-N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*3.5),(R2+R1)/2*sin(taud*3.5));
mi_addblocklabel((R2+R1)/2*cos(taud*4.5),(R2+R1)/2*sin(taud*4.5));
mi_selectlabel((R2+R1)/2*cos(taud*3.5),(R2+R1)/2*sin(taud*3.5));
mi_selectlabel((R2+R1)/2*cos(taud*4.5),(R2+R1)/2*sin(taud*4.5));
mi_setblockprop('Bobine',1,0,'Phase b',0,4,N);
mi_clearselected;
mi_addblocklabel((R2+R1)/2*cos(taud*5.5),(R2+R1)/2*sin(taud*5.5));
mi_selectlabel((R2+R1)/2*cos(taud*5.5),(R2+R1)/2*sin(taud*5.5));
mi_setblockprop('Bobine',1,0,'Phase a',0,2,-N);
mi_clearselected;
mi_addblocklabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_selectlabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_setblockprop('Toles Stator',1,0,0,0,1,0);
mi_clearselected;
mi_selectsegment(R2,0);
mi_selectsegment(R2*cos(taup),R2*sin(taup));
mi_setsegmentprop('antiper1',0,1,0,1);
mi_clearselected;
mi_selectsegment((Ra-e/6),0);
mi_selectsegment((Ra-e/6)*cos(taup),(Ra-e/6)*sin(taup));
mi_setsegmentprop('antiper2',0,1,0,1);
mi_clearselected;
mi_selectarcsegment(R3*cos(taup/2),R3*sin(taup/2));
mi_setarcsegmentprop(5,'Fond culasse',0,1);
mi_clearselected;
% rotor
R1 = Ra-2*e/3;
R2 = Ra-e;
R3 = R2-ea;
R4 = R3-ecr;
theta1 = (1-alphaa)*taup/2;
theta2 = (1+alphaa)*taup/2;
mi_drawpolyline([R4,0;R3,0;R1,0]);
mi_drawpolyline([R4*cos(taup),R4*sin(taup);R3*cos(taup),R3*sin(taup); ...
R1*cos(taup),R1*sin(taup)]);
mi_drawline(R3*cos(theta1),R3*sin(theta1),R2*cos(theta1),R2*sin(theta1));
mi_drawline(R3*cos(theta2),R3*sin(theta2),R2*cos(theta2),R2*sin(theta2));
mi_addarc(R4,0,R4*cos(taup),R4*sin(taup),taup*180/pi,5);
mi_addarc(R3,0,R3*cos(theta1),R3*sin(theta1),theta1*180/pi,5);
mi_addarc(R3*cos(theta2),R3*sin(theta2),R3*cos(taup),R3*sin(taup), ...
theta1*180/pi,5);
mi_addarc(R3*cos(theta1),R3*sin(theta1),R3*cos(theta2),R3*sin(theta2), ...
alphaa*taup*180/pi,5);
mi_addarc(R2*cos(theta1),R2*sin(theta1),R2*cos(theta2),R2*sin(theta2), ...
alphaa*taup*180/pi,1);
mi_addarc(R1,0,R1*cos(taup),R1*sin(taup),taup*180/pi,1);
mi_addblocklabel((R2+R3)/2*cos(theta1/2),(R2+R3)/2*sin(theta1/2));
mi_selectlabel((R2+R3)/2*cos(theta1/2),(R2+R3)/2*sin(theta1/2));
mi_setblockprop('Air',1,0,0,0,5,0);
mi_clearselected;
mi_addblocklabel((R4+R3)/2*cos(taup/2),(R4+R3)/2*sin(taup/2));
mi_selectlabel((R4+R3)/2*cos(taup/2),(R4+R3)/2*sin(taup/2));
mi_setblockprop('XC10',1,0,0,0,6,0);
mi_clearselected;
mi_addblocklabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_selectlabel((R2+R3)/2*cos(taup/2),(R2+R3)/2*sin(taup/2));
mi_setblockprop('NdFeB',1,0,0,'theta',6,0);
mi_clearselected;
mi_selectsegment(R2,0);
mi_selectsegment(R2*cos(taup),R2*sin(taup));
mi_setsegmentprop('antiper3',0,1,0,5);
mi_clearselected;
mi_selectsegment((R4+R3)/2,0);
mi_selectsegment((R4+R3)/2*cos(taup),(R4+R3)/2*sin(taup));
mi_setsegmentprop('antiper4',0,1,0,5);
mi_clearselected;
mi_selectarcsegment(R4*cos(taup/2),R4*sin(taup/2));
mi_setarcsegmentprop(5,'Fond culasse',0,1);
mi_clearselected;
mi_selectarcsegment((Ra-2*e/3)*cos(taup/2),(Ra-2*e/3)*sin(taup/2));
mi_selectarcsegment((Ra-e/3)*cos(taup/2),(Ra-e/3)*sin(taup/2));
mi_setarcsegmentprop(1,'Bande Roulement',0,1);
mi_clearselected;
mi_zoomnatural;
mi_saveas('masap.FEM')
ntheta = 30; % nombre de positions
dtheta_rad = pi/p/ntheta;
dtheta_deg = dtheta_rad*180/pi; % FEMM travaille en degres...
for n = 1:ntheta
mi_analyse();
mi_loadsolution();
mo_hidepoints;
mo_showdensityplot(0,0,2,0,'mag');
mo_savebitmap(char("imagesMag\B"+n+".bmp"));
mi_modifyboundprop('Bande Roulement',10,angRot+n*dtheta_deg);
end
mi_modifyboundprop('Bande Roulement',10,angRot); % retour position initiale
- Python :
import numpy as np
import femm
# Donnees probleme (toutes les longueurs sont en cm)
pp = 3 # nombre de paires de poles
Lz = 20 # longueur
Ra = 10 # rayon d'alesage
alphae = 0.5 # larg. ang. encoche
alphai = 0.2 # larg. ang. isthme
he = 3 # hauteur encoche
hi = 0.25 # hauteur isthme
ecs = 1 # epaisseur culasse stator
e = 0.2 # entrefer
ea = 0.6 # epaisseur aimant
ecr = 1.5 # epaisseur culasse rotor
alphaa = (9-alphai)/12; # coef. arc polaire
taup = np.pi/p # pas polaire
taud = taup/6 # pas dentaire
N = 25 # nombre de spires
Ieff = 0 # valeur eff courant d'alim.
w = 2*np.pi*50 # pulsation
Ia = 0
Ib = 0
Ic = 0
Omega = w/p # vitesse
angRot = 0 # position rotor : 0 (plus simple a reperer car position geometrie)
angStat = 0 # on laisse 0 : centre sur phase a
femm.openfemm()
femm.newdocument(0)
femm.mi_probdef(0,'centimeters','planar',1e-8,Lz)
# Materiaux
femm.mi_getmaterial('Air')
femm.mi_getmaterial('M-19 Steel')
femm.mi_modifymaterial('M-19 Steel',0,'Toles Stator')
femm.mi_getmaterial('1010 Steel')
femm.mi_modifymaterial('1010 Steel',0,'XC10')
femm.mi_getmaterial('Copper')
femm.mi_modifymaterial('Copper',0,'Bobine')
femm.mi_getmaterial('N30')
femm.mi_modifymaterial('N30',0,'NdFeB')
# Sources
femm.mi_addcircprop('Phase a',Ia,1)
femm.mi_addcircprop('Phase b',Ib,1)
femm.mi_addcircprop('Phase c',Ic,1)
# CL
femm.mi_addboundprop('Fond culasse',0,0,0,0)
femm.mi_addboundprop('antiper1',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper2',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper3',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('antiper4',0,0,0,0,0,0,0,0,5,0,0)
femm.mi_addboundprop('Bande Roulement',0,0,0,0,0,0,0,0,7,angRot,angStat)
# Attention : bug dans femm.mi_addboundprop.m, on doit rajouter :
femm.mi_modifyboundprop('Bande Roulement',10,angRot)
# stator
R1 = Ra+hi
R2 = R1+he
R3 = R2+ecs
theta1 = (1-alphai)*taud/2
theta2 = (1-alphae)*taud/2
theta3 = (1+alphae)*taud/2
theta4 = (1+alphai)*taud/2
femm.mi_addnode(Ra,0)
femm.mi_drawarc(Ra,0,Ra*np.cos(theta1),Ra*np.sin(theta1),theta1*180/np.pi,1)
femm.mi_drawline(Ra*np.cos(theta1),Ra*np.sin(theta1),R1*np.cos(theta1),R1*np.sin(theta1))
femm.mi_drawline(R1*np.cos(theta1),R1*np.sin(theta1),R1*np.cos(theta2),R1*np.sin(theta2))
femm.mi_drawline(R1*np.cos(theta2),R1*np.sin(theta2),R2*np.cos(theta2),R2*np.sin(theta2))
femm.mi_drawarc(R2*np.cos(theta2),R2*np.sin(theta2),R2*np.cos(theta3),R2*np.sin(theta3),
alphae*taud*180/np.pi,5)
femm.mi_drawline(R2*np.cos(theta3),R2*np.sin(theta3),R1*np.cos(theta3),R1*np.sin(theta3))
femm.mi_drawline(R1*np.cos(theta3),R1*np.sin(theta3),R1*np.cos(theta4),R1*np.sin(theta4))
femm.mi_drawline(R1*np.cos(theta4),R1*np.sin(theta4),Ra*np.cos(theta4),Ra*np.sin(theta4))
femm.mi_drawarc(Ra*np.cos(theta4),Ra*np.sin(theta4),Ra*np.cos(taud),Ra*np.sin(taud),
theta1*180/np.pi,1)
r1 = 0.1
femm.mi_createradius(R1*np.cos(theta2),R1*np.sin(theta2),r1)
femm.mi_createradius(R1*np.cos(theta3),R1*np.sin(theta3),r1)
r2 = 0.4
femm.mi_createradius(R2*np.cos(theta2),R2*np.sin(theta2),r2)
femm.mi_createradius(R2*np.cos(theta3),R2*np.sin(theta3),r2)
femm.mi_addsegment(R1*np.cos(theta1),R1*np.sin(theta1),R1*np.cos(theta4),R1*np.sin(theta4))
femm.mi_selectgroup(0)
femm.mi_copyrotate(0, 0, taud*180/np.pi, 5 )
femm.mi_drawline(Ra,0,R3,0)
femm.mi_drawline(Ra*np.cos(taup),Ra*np.sin(taup), R3*np.cos(taup),R3*np.sin(taup))
femm.mi_drawarc(R3,0,R3*np.cos(taup),R3*np.sin(taup),taup*180/np.pi,5)
femm.mi_drawline(Ra,0,Ra-e/3,0)
femm.mi_drawline(Ra*np.cos(taup),Ra*np.sin(taup),(Ra-e/3)*np.cos(taup),(Ra-e/3)*np.sin(taup))
femm.mi_drawarc((Ra-e/3),0,(Ra-e/3)*np.cos(taup),(Ra-e/3)*np.sin(taup),taup*180/np.pi,1)
femm.mi_addblocklabel((Ra+R1)/2*np.cos(taud/2),(Ra+R1)/2*np.sin(taud/2))
femm.mi_selectlabel((Ra+R1)/2*np.cos(taud/2),(Ra+R1)/2*np.sin(taud/2))
femm.mi_setblockprop('Air',1,0,0,0,0,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud/2),(R2+R1)/2*np.sin(taud/2))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud/2),(R2+R1)/2*np.sin(taud/2))
femm.mi_setblockprop('Bobine',1,0,'Phase a',0,2,N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*1.5),(R2+R1)/2*np.sin(taud*1.5))
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*2.5),(R2+R1)/2*np.sin(taud*2.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*1.5),(R2+R1)/2*np.sin(taud*1.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*2.5),(R2+R1)/2*np.sin(taud*2.5))
femm.mi_setblockprop('Bobine',1,0,'Phase c',0,3,-N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*3.5),(R2+R1)/2*np.sin(taud*3.5))
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*4.5),(R2+R1)/2*np.sin(taud*4.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*3.5),(R2+R1)/2*np.sin(taud*3.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*4.5),(R2+R1)/2*np.sin(taud*4.5))
femm.mi_setblockprop('Bobine',1,0,'Phase b',0,4,N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R1)/2*np.cos(taud*5.5),(R2+R1)/2*np.sin(taud*5.5))
femm.mi_selectlabel((R2+R1)/2*np.cos(taud*5.5),(R2+R1)/2*np.sin(taud*5.5))
femm.mi_setblockprop('Bobine',1,0,'Phase a',0,2,-N)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('Toles Stator',1,0,0,0,1,0)
femm.mi_clearselected()
femm.mi_selectsegment(R2,0)
femm.mi_selectsegment(R2*np.cos(taup),R2*np.sin(taup))
femm.mi_setsegmentprop('antiper1',0,1,0,1)
femm.mi_clearselected()
femm.mi_selectsegment((Ra-e/6),0)
femm.mi_selectsegment((Ra-e/6)*np.cos(taup),(Ra-e/6)*np.sin(taup))
femm.mi_setsegmentprop('antiper2',0,1,0,1)
femm.mi_clearselected()
femm.mi_selectarcsegment(R3*np.cos(taup/2),R3*np.sin(taup/2))
femm.mi_setarcsegmentprop(5,'Fond culasse',0,1)
femm.mi_clearselected()
# rotor
R1 = Ra-2*e/3
R2 = Ra-e
R3 = R2-ea
R4 = R3-ecr
theta1 = (1-alphaa)*taup/2
theta2 = (1+alphaa)*taup/2
femm.mi_drawline(R4,0,R3,0)
femm.mi_drawline(R3,0,R1,0)
femm.mi_drawline(R4*np.cos(taup),R4*np.sin(taup),R3*np.cos(taup),R3*np.sin(taup))
femm.mi_drawline(R3*np.cos(taup),R3*np.sin(taup),R1*np.cos(taup),R1*np.sin(taup))
femm.mi_drawline(R3*np.cos(theta1),R3*np.sin(theta1),R2*np.cos(theta1),R2*np.sin(theta1))
femm.mi_drawline(R3*np.cos(theta2),R3*np.sin(theta2),R2*np.cos(theta2),R2*np.sin(theta2))
femm.mi_addarc(R4,0,R4*np.cos(taup),R4*np.sin(taup),taup*180/np.pi,5)
femm.mi_addarc(R3,0,R3*np.cos(theta1),R3*np.sin(theta1),theta1*180/np.pi,5)
femm.mi_addarc(R3*np.cos(theta2),R3*np.sin(theta2),R3*np.cos(taup),R3*np.sin(taup),
theta1*180/np.pi,5)
femm.mi_addarc(R3*np.cos(theta1),R3*np.sin(theta1),R3*np.cos(theta2),R3*np.sin(theta2),
alphaa*taup*180/np.pi,5)
femm.mi_addarc(R2*np.cos(theta1),R2*np.sin(theta1),R2*np.cos(theta2),R2*np.sin(theta2),
alphaa*taup*180/np.pi,1)
femm.mi_addarc(R1,0,R1*np.cos(taup),R1*np.sin(taup),taup*180/np.pi,1)
femm.mi_addblocklabel((R2+R3)/2*np.cos(theta1/2),(R2+R3)/2*np.sin(theta1/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(theta1/2),(R2+R3)/2*np.sin(theta1/2))
femm.mi_setblockprop('Air',1,0,0,0,5,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R4+R3)/2*np.cos(taup/2),(R4+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R4+R3)/2*np.cos(taup/2),(R4+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('XC10',1,0,0,0,6,0)
femm.mi_clearselected()
femm.mi_addblocklabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_selectlabel((R2+R3)/2*np.cos(taup/2),(R2+R3)/2*np.sin(taup/2))
femm.mi_setblockprop('NdFeB',1,0,0,'theta',6,0)
femm.mi_clearselected()
femm.mi_selectsegment(R2,0)
femm.mi_selectsegment(R2*np.cos(taup),R2*np.sin(taup))
femm.mi_setsegmentprop('antiper3',0,1,0,5)
femm.mi_clearselected()
femm.mi_selectsegment((R4+R3)/2,0)
femm.mi_selectsegment((R4+R3)/2*np.cos(taup),(R4+R3)/2*np.sin(taup))
femm.mi_setsegmentprop('antiper4',0,1,0,5)
femm.mi_clearselected()
femm.mi_selectarcsegment(R4*np.cos(taup/2),R4*np.sin(taup/2))
femm.mi_setarcsegmentprop(5,'Fond culasse',0,1)
femm.mi_clearselected()
femm.mi_selectarcsegment((Ra-2*e/3)*np.cos(taup/2),(Ra-2*e/3)*np.sin(taup/2))
femm.mi_selectarcsegment((Ra-e/3)*np.cos(taup/2),(Ra-e/3)*np.sin(taup/2))
femm.mi_setarcsegmentprop(1,'Bande Roulement',0,1)
femm.mi_clearselected()
femm.mi_zoomnatural()
femm.mi_saveas('masap.FEM')
ntheta = 30 # nombre de positions
dtheta_rad = np.pi/p/ntheta
dtheta_deg = dtheta_rad*180/np.pi # FEMM travaile en degres...
for n in range(ntheta):
femm.mi_analyze()
femm.mi_loadsolution()
femm.mo_hidepoints()
femm.mo_showdensityplot(0,0,2,0,'mag')
femm.mo_savebitmap("imagesMag{}.bmp".format(n+1))
femm.mi_modifyboundprop('Bande Roulement',10,angRot+n*dtheta_deg)
# Retour position initiale_
femm.mi_modifyboundprop('Bande Roulement',10,angRot)
Avec les résultats obtenus, on peut réaliser la petite animation suivante :
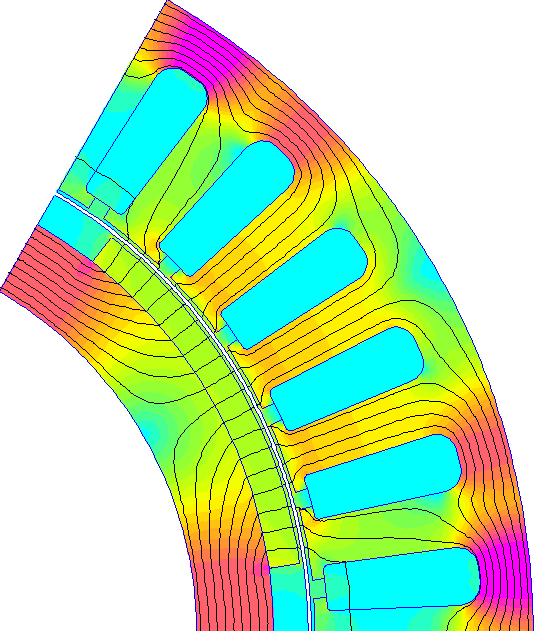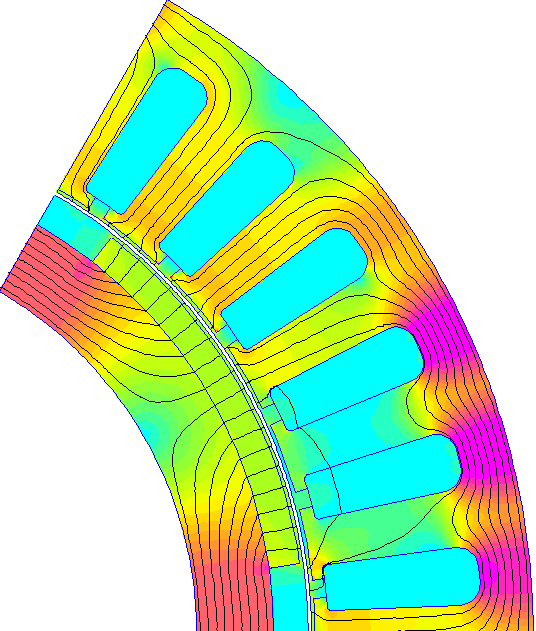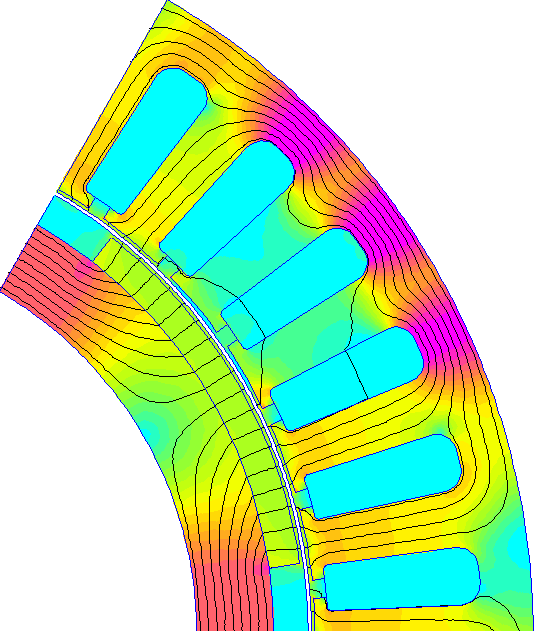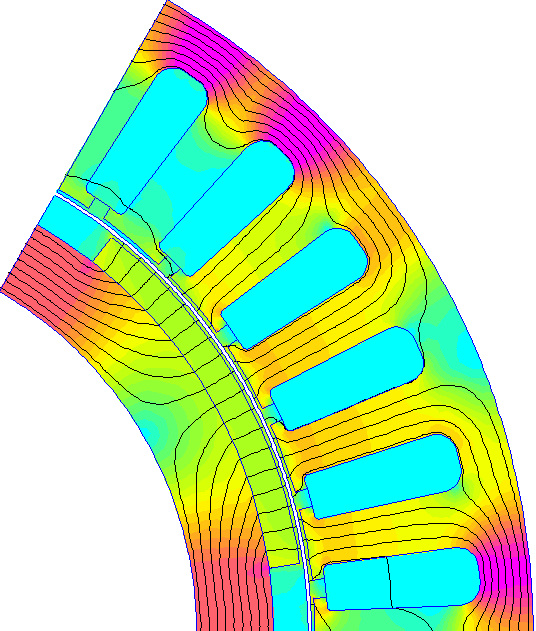
➤ Analysez le programme fourni et commentez les différentes parties.
Exploitation
Modèle externe : Flux, fem, et estimation du couple
➤ Modifiez le programme précédent pour calculer les flux à vide
Astuce : Pour calculer les flux, regardez la commande
mo_getcircuitproperties.
➤ Dérivez les courbes obtenues pour en déduire les fem (forces électromotrices) à vide :
➤ Déterminez l'angle de calage \(\psi\) de la machine permettant d'avoir des courants d'alimentation en phase avec les fem (fonctionnement à couple max) dans le cas d'une alimentation sinusoïdale classique de la forme :
$$\left\{\begin{aligned}I_a(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi\right)\\I_b(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi-\frac{2\pi}{3}\right)\\I_c(t) &= I_{\text{eff}} \sqrt{2} \cos\left(\omega\,t-\psi+\frac{2\pi}{3}\right)\end{aligned}\right.$$
➤ Tracez alors l'allure de l'estimation du couple issue des fem à vide en fonction de la position du rotor :
On rappelle la formule : $$\Gamma_{\text{em}} = \frac{1}{\Omega} \sum_{k = (a,b,c)} E_k \cdot I_k$$
Exemple de résultat :
Calcul du couple par éléments finis
Le calcul du couple exercé sur le rotor se fait de la même façon que celui de la force vu pour la ventouse :
-
Par le tenseur de Maxwell moyenné : basé sur la technique de la « coquille d'œuf » vue précédemment.
La densité surfacique de force est issue du tenseur des contraintes électromagnétiques de Maxwell, on utilise comme surface \(S\) un cylindre passant dans l'entrefer, et on obtient pour le moment du couple : \[ \Gamma = \iint_{S}\,\left( {\bf r} \wedge \left(\overline{\overline{{\bf T}}}\cdot{\bf n}\right) \right) \cdot {\bf u_z} \, \text{d} S\] Pour notre problème 2D, on peut considérer un arc de cercle \(C\) passant dans l'entrefer, pour obtenir : \[\Gamma = 2\,p\,L_z\,\int_{C}\,\left( {\bf r} \wedge\overline{\overline{{\bf T}}}\cdot{\bf n}\right) \cdot {\bf u_z} \, \text{d}l\] Une expression moyennée dans une couche d'éléments dans l'air entourant le rotor peut-être directement calculée par FEMM.
On sélectionne les blocs correspondants à la culasse rotorique et l'aimant (groupe 6 dans le programme fourni), et on appliquemo_blockintegral(22)pour avoir le terme intégral. -
Par une méthode des travaux virtuels (avec dérivée de la coénergie) :
Vous avez vu dans le premier EC du bloc et en cours de Machines Électrique que le couple était la dérivée de la coénergie par rapport à la position angulaire à courant constant : \[\Gamma = \left.\frac{\partial\,\widetilde{W}}{\partial \theta}\right|_{I\,\text{constant}}\] On calcule donc la coénergie dans tout le pôle de la machine pour 2 positions : \(\theta_k\) et \(\theta_k+\Delta\theta\), à courant constant. Puis, on obtient le couple par : \[ \Gamma \left(\theta_k\right) = 2\,p\,\frac{\widetilde{W}(\theta_k+\Delta \theta)-\widetilde{W}(\theta_k)}{\Delta\theta}\]
➤ En utilisant une alimentation identique au modèle externe ci-dessus, calculez puis tracez le couple en fonction de la position du rotor, en superposant les courbes correspondant aux deux méthodes :
➤ Commentez les allures des deux courbes de couple (par le modèle externe et par la MEF).
Félicitations !
Si vous avez tout assimilé et tout compris vous êtes devenu un bon utilisateur de FEMM. Avec de la pratique, vous pourrez même devenir un power user !