Runge-Kutta d'ordre 2
Bien qu'elle ne soit pas aussi employée que la méthode d'ordre 4 (RK4), la preuve de la méthode de Runge-Kutta d'ordre 2 (RK2) est plus facile à comprendre et illustre clairement les principes énoncés ci-avant.
\(~\)
On rappelle donc le problème à résoudre :
\(\left\{ \begin{array}{l} y'(x) = f(x,y(x))\\ y(x_0) = y_0 \end{array} \right.~~~~~(P)\)
On commence en écrivant le développement en série de Taylor à l'ordre 2 :
\(y(x+h) = y(h) + h~y'(x) +\frac{h^2}{2}~y''(x) + O(h^3)\)
On va ensuite exprimer les dérivées \(y'(x)\) et \(y''(x)\) en fonction de \(f(x,y)\) et de ses dérivées partielles par rapport à \(x\) et \(y\).
On sait que : \(y'(x) = f\left(x,y(x)\right)\)
On peut en déduire :
\(\begin{array}{r l} y''(x) &=\displaystyle {\Huge \mathstrut}\frac{d}{dx}\big[f(x,y(x))\big]\\ &= \displaystyle{\Huge \mathstrut}\frac{d\,f(x,y(x))}{dx} + \frac{d\,f(x,y(x))}{dy}\cdot\frac{d\,y(x)}{dx} \\ &= \displaystyle{\Huge \mathstrut}\frac{d\,f(x,y)}{dx} + \frac{d\,f(x,y)}{dy}\cdot y'(x) \\ &= \displaystyle{\Huge \mathstrut}\frac{d\,f(x,y)}{dx} + \frac{d\,f(x,y)}{dy}\cdot f(x,y(x)) \end{array}\)
On substitue alors ces deux expressions dans le développement de Taylor précédent, et on obtient :
\(y(x+h) = y(h) + h~f(x,y) +\frac{h^2}{2}~\frac{d\,f(x,y)}{dx} + \frac{h^2}{2}~\frac{d\,f(x,y)}{dy}\cdot f(x,y(x)) + O(h^3)\)
L'idée qu'on eu Runge et Kutta est d'écrire une combinaison linéaire de deux valeurs de la fonction \(f\) pour exprimer \(y(x+h)\) :
\(y(x+h) = y(x) + A\,h\,f_0 + B\,h\,f_1~~~~~(E)\)
avec :
\(\left\{ \begin{array}{l} f_0 = f(x,y(x)) \\ f_1 = f(x + P h, y(x)+Qhf_0) \end{array} \right.\)
Ils ont ensuite appliqué à \(f_1\) le développement de Taylor (à l'ordre 1) d'une fonction de deux variables :
\(\begin{array}{r l} f_1 &= f(x,y) + P h~\frac{d\,f(x,y)}{dx} + Q h f_0~\frac{d\,f(x,y)}{dy} + O(h) \\ & = f(x,y) + P h~\frac{d\,f(x,y)}{dx} + Q h~\frac{d\,f(x,y)}{dy}~f(x,y(x)) + O(h) \end{array}\)
En reportant les expressions de \(f_0\) et \(f_1\) dans \((E)\) :
\(y(x+h) = y(x) + (A+B)h~f(x,y) + B P h^2~\frac{d\,f(x,y)}{dx} + B Q h^2~\frac{d\,f(x,y)}{dy}~f(x,y) + O(h^3)\)
En identifiant terme à terme les deux développement faisant intervenir les dérivées partielles, on trouve :
\(\left\{ \begin{array}{l} A + B = 1 \\ B P = {\Huge \mathstrut}\tfrac{1}{2}\\ B Q = {\Huge \mathstrut}\tfrac{1}{2} \end{array} \right.\)
Ainsi, avec des valeurs de \(A,~B,~P\) et \(Q\) vérifiant les relations ci-dessus, la solution de \((P)\) fournie par la méthode de Runge-Kutta d'ordre 2 aura la même approximation que celle fournie par le développement en série de Taylor.
\(~\)
Puisqu'on n'a que 3 équations pour 4 inconnues, on peut choisir arbitrairement un des coefficients. On prend alors \(A = 0\), et ainsi \(B = 1\), et \(P = Q = \tfrac{1}{2}\).
Dans ce cas, le schéma correspondant est :
\(y_{k+1} = y_k + h \cdot f_1\), avec : \(\left\{ \begin{array}{l} f_0 = f(x_k,y_k) \\ {\Huge \mathstrut} f_1 = f(x_k+\frac{h}{2}, ~y_k + \frac{h}{2}f_0) \end{array} \right.\)
\(~\)
Graphiquement, le procédé est représenté sur la figure ci-dessous.
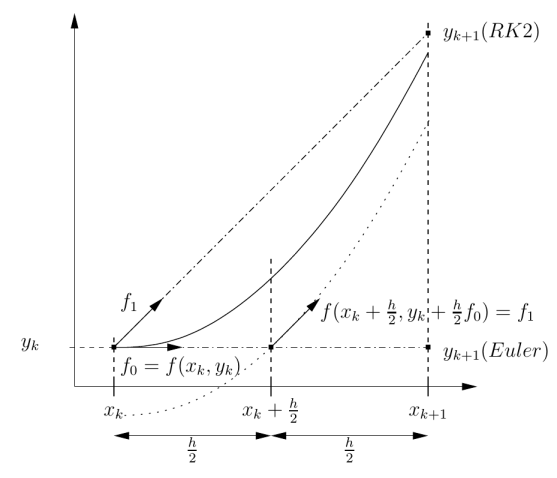
Remarque :
Parfois la méthode RK2 est aussi appelée méthode de la tangente améliorée ou encore méthode d'Euler modifiée.
Point de vue algorithmique :
Complément :
C'est la même technique qui amène aux méthodes de Runge-Kutta d'ordre \(n\). La plus populaire d'entre elles, parce qu'elle assure un bon compromis entre l'effort de programmation et les performances qu'elle fournie est la méthode de Runge-Kutta d'ordre 4 (RK4).
