Runge-Kutta d'ordre 4
Cette méthode fournit une solution approchée du problème \((P)\) avec une erreur du même ordre que celle obtenue par le développement en série de Taylor d'ordre 4.
Schéma de RK4 :
Elle est basée sur le schéma suivant :
\(y_{k+1} = y_k + \frac{h}{6}~\bigg(f_1 + 2 f_2 + 2 f_3 + f_4 \bigg)\), avec :
\(\left\{ \begin{array}{l} f_1 = f(x_k,y_k) \\ {\Huge \mathstrut} f_2 = f(x_k+\frac{h}{2}, ~y_k + \frac{h}{2}f_1)\\ {\Huge \mathstrut} f_3 = f(x_k+\frac{h}{2}, ~y_k + \frac{h}{2}f_2)\\ {\Huge \mathstrut} f_4 = f(x_k+ h, ~y_k + h f_3)\\ \end{array} \right.\)
Graphiquement, le procédé est représenté sur la figure ci-dessous.
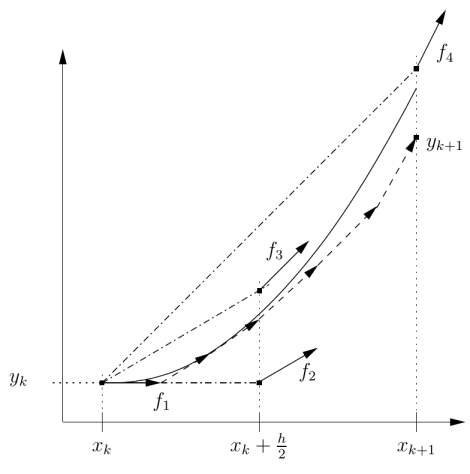
Fondamental : Théorème
La suite des approximations successives produites par la méthode de Runge-Kutta d'ordre 4 est de la forme :
\(\epsilon_k = ||y(x_k)- y_k || = O(h^4)\)
Remarque :
RK4 est souvent représenté dans la littérature sous une autre forme équivalente :
\(y_{k+1} = y_k + \frac{1}{6}~\bigg(K_1 + 2 (K_2 + K_3) + K_4 \bigg)\), avec :
\(\left\{ \begin{array}{l} K_1 = h \cdot f(x_k,y_k) \\ {\Huge \mathstrut} K_2 = h \cdot f(x_k+\frac{h}{2}, ~y_k + \frac{K_1}{2})\\ {\Huge \mathstrut} K_3 = h \cdot f(x_k+\frac{h}{2}, ~y_k + \frac{K_2}{2})\\ {\Huge \mathstrut} K_4 = h \cdot f(x_k+ h, ~y_k + K_3)\\ \end{array} \right.\)
L'algorithme de résolution correspondant est :
