Circuit RL

Description du problème et étude préliminaire

On étudie le dispositif illustré par la figure suivante : un circuit RL alimenté par une source de tension continue E via un interrupteur. On ferme l'interrupteur à l'instant \(t=0\), et on cherche à calculer l'établissement du courant dans le circuit (et donc la tension au bornes de la résistance).

Les valeurs numériques des différentes grandeurs sont :

  • E = 200 V

  • L = 10 mH

  • R = 10 Ω

Question

Donner l'équation différentielle à laquelle obéit le courant, et sa condition initiale.

Indice

On pourra utiliser la loi des mailles et se rappeler la tension aux bornes d'une inductance : \(v_L(t) = L\,\frac{d\,i}{dt}\).

Solution

Pour \(t\geq 0\), \(E = R\,i(t) + L\,\frac{d\,i(t)}{dt}\)

Initialement, le circuit est ouvert : \(i(0) = 0\)

Question

Résoudre analytiquement l'équation précédente.

Indice

La solution particulière est évidente, elle correspond au régime permanent.

Solution

\(i(t) = \frac{E}{R}\,\left(1-e^{-\frac{R}{L}\,t}\right)\)

Implantation sous Matlab ou Octave

Dans la suite, nous allons utiliser un des deux logiciels pour tracer cette solution analytique. Ouvrez celui que vous avez choisi et enregistrez un nouveau script (on l’appellera par exemple CircuitRL.m)

Pour commencer le script, on procède à un petit nettoyage après un en-tête rapide (les "%" permettent d'ajouter des commentaires) :

1
% Fichier CircuitRL.m correspondant au 1er exercice du TP
2
%  Circuit RL soumis a un echelon de tension
3
4
clear       % Nettoyage du Workspace
5
close all   % Fermeture des fenetres restees ouvertes
6
clc         % Nettoyage du terminal de commande
7
 
On définit ensuite les grandeurs du problème (les ";" clôturent l'instruction courante et évitent un affichage dans le terminal de commande) :
1
L = 100e-3;  % H
2
R = 10;     % Ohm
3
E = 200;    % V (~ 2*sqrt(2)/pi*230) 
4
5
t_ini = 0;       % instant initial
6
t_fin = 10*L/R;  % instant final = 10 fois la constante de temps 
Nous devons ensuite définir 2 vecteurs pour pouvoir tracer la solution analytique :
  • celui contenant les valeurs de temps (t_ana) ;
  • celui contenant les valeurs de courant correspondantes (i_ana). On utilisera la notation vectorielle pour simplifier l'écriture, d'où le ".*" devant "t_ana" pour effectuer une opération terme à terme.
1
npoints_ana = 10000;                           % nombre de points utilisés pour le trace
2
t_ana = t_ini:(t_fin-t_ini)/(npoints_ana-1):t_fin;  % vecteur de temps 
3
i_ana = E/R*(1-exp(-R/L.*t_ana));                   % valeurs de courant correspondantes
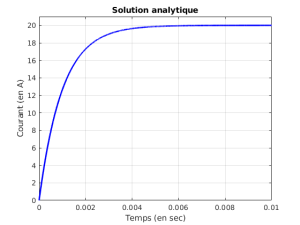
On crée ensuite une figure pour le tracé de i_ana en fonction de t_ana :
1
figure(1)                                    % nouvelle figure 1
2
plot(t_ana,i_ana,'b-','LineWidth',2)         % trace avec une ligne d'epaisseur 2
3
grid on                                      % affiche la grille
4
xlabel('Temps (en sec)')                     % label des abscisses
5
ylabel('Courant (en A)')                     % label des ordonnees 
6
title('Solution analytique')                 % titre de la figure 
7
axis([t_ini, t_fin, 0, round(max(i_ana))+1]) % echelle des axes
On obtient alors la figure :
Question
Mettre le problème sous forme résolue et implanter la méthode d'Euler dans le fichier *.m pour calculer les vecteurs t_euler et i_euler contenant les résultats correspondants.
Solution
Forme résolue
On a : \(i'(t) = f(t,i)\) et \(i(0) = 0\) avec :
\(f(t,i) = -\frac{R}{L}\,i +\frac{E}{L}\)
Implantation
On programme l'algorithme de la méthode d'Euler : cliquez ici pour rappel[1].
On commence par définir la fonction donnant l'équation différentielle et la condition initiale :
1
f = @(t,i) -R/L*i + E/L;  % fonction de t et de i definissant l'equa. diff.
2
i0 = 0;                   % condition initiale
On implante directement l'algorithme (il faut juste penser à un décalage d'indice car Matlab ou Octave ne peuvent que commencer à 1) :
1
n = 20;                   % nombre de pas de calcul
2
h = (t_fin-t_ini)/n; 
3
4
5
% initialisation 
6
t_euler = zeros(1,n+1);
7
i_euler = zeros(1,n+1);
8
t_euler(1) = t_ini;       % condition initiale (sur t)
9
i_euler(1) = i0;          % condition initiale (sur i)
10
for k = 2:n+1             % on boucle de 2 a n+1 car on ne peut pas indicer a partir de zero  
11
    i_euler(k) = i_euler(k-1) + h*f(t_euler(k-1),i_euler(k-1));
12
    t_euler(k) = t_euler(k-1)+h;
13
end
Tracé des nouveaux résultats
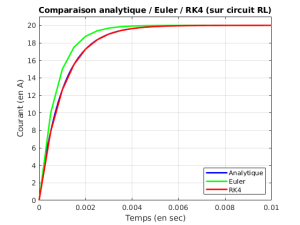
On va modifier la figure courante pour rajouter le tracé de i_euler en fonction de t_euler :
1
hold on                 % on rajoute le trace sur la figure courante 
2
plot(t_euler,i_euler,'g','LineWidth',2)     % trace avec une ligne verte 
3
title('Comparaison analytique / Euler')     % modification du titre de la figure 
Question
Mettre en œuvre la méthode de Runge-Kutta 4 pour calculer aussi t_RK4 et i_RK4.
Solution
Implantation
On implante l'algorithme tel que donné dans la partie précédente : cliquez ici pour rappel[2].
On garde le même pas que pour la méthode d'Euler, il reste :
1
t_RK4 = zeros(1,n);
2
i_RK4 = zeros(1,n);
3
t_RK4(1) = t_ini;
4
i_RK4(1) = i0;
5
for k = 2:n+1
6
    f1 = f( t_RK4(k-1) , i_RK4(k-1) ); 
7
    f2 = f( t_RK4(k-1)+h/2 , i_RK4(k-1)+h/2*f1 );
8
    f3 = f( t_RK4(k-1)+h/2 , i_RK4(k-1)+h/2*f2 );
9
    f4 = f( t_RK4(k-1)+h   , i_RK4(k-1)+h*f3 );
10
    i_RK4(k) = i_RK4(k-1) + h/6*(f1+2*f2+2*f3+f4);
11
    t_RK4(k) = t_RK4(k-1)+h;
12
end
Tracé final
On rajoute le dernier tracé et une légende
1
plot(t_RK4,i_RK4,'r','LineWidth',2)                              % en rouge
2
title('Comparaison analytique / Euler / RK4 (sur circuit RL)')
3
legend('Analytique','Euler','RK4','Location','SouthEast')        % légende en bas à droite (sud-est)
On obtient alors :
Question
Tester et comparer les performances des méthodes en modifiant le pas de calcul (en modifiant la valeur du nombre de pas n).
Indice
On pourra essayer n = 10, 20 ou 100...