Filtre RL

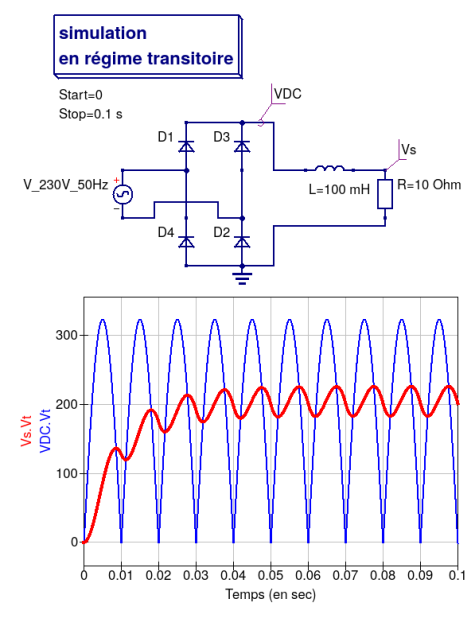
L'inductance du circuit précédent est utilisée derrière un pont redresseur avant d'alimenter une résistance de charge R. Le dispositif étudié est ainsi décrit par la figure ci-dessous : la tension réseau (230 V / 50 Hz) est redressée par un pont de diode supposé idéal qui alimente la charge via l'inductance. Il serait très pénible de trouver une solution analytique au problème, donc pour information et vérification ultérieure, on trace les formes d'onde de la tension redressée (VDC) et de celle dans la charge (Vs) avec un logiciel libre de simulation de circuits électriques (Qucs ou sa variante Qucs-S basée sur SPICE).

Le pont étant idéal, on peut considérer que la tension VDC est égale à la valeur absolue de la tension d'entrée, soit :

\(\text{VDC} = \left|V_{\text{eff}}\sqrt{2} \sin(\omega t)\right|\), avec \(\omega = 2\pi\,f~~~\) (\(V_{\text{eff}} = 230\,\text{V}\), \(f = 50\,\text{Hz}\)).

Question

À l'aide du fichier de la partie précédente, créer un fichier FiltreRL.m (par exemple) qui permettra de résoudre le problème à l'aide des deux méthodes (Euler et RK4). Commencer par définir les grandeurs, ainsi que les fonctions associées.

Indice

Le début est identique à celui de CircuitRL.m, si ce n'est la fonction "VDC(t)" et la fonction "f" associée à l'équation différentielle (VDC y remplace E).

Solution

1
% Fichier FiltreRL.m correspondant au 2eme exercice du TP
2
%  Filtre RL derriere un pont de diodes
3
4
clear       % Nettoyage du Workspace
5
close all   % Fermeture des fenetres restees ouvertes
6
clc         % Nettoyage du terminal de commande
7
 
8
L = 100e-3;    % H
9
R = 10;        % Ohm
10
11
freq = 50;     % Hz
12
w = 2*pi*freq; % s^-1
13
VDC = @(t) abs(230*sqrt(2)*sin(w*t)); % V
14
15
f = @(t,i) -R/L*i + VDC(t)/L;  
16
i0 = 0;
Calcul de la tension de sortie avec Euler
Nous allons maintenant résoudre notre équation différentielle avec la méthode d'Euler. La tension source VDC étant périodique (de période \(T = \frac{1}{2\,f}\), le régime permanent sera lui aussi T-périodique. Il est donc judicieux de définir le pas de calcul h à partir de cette période. Soit :
1
T = 1/freq/2;  % periode de la source
2
nbp = 10;      % nombre de periodes pour le calcul
3
t_ini = 0.;    % instant initiel
4
t_fin = nbp*T; % instant final = nbp periodes
5
6
nbpp = 10;     % nombre de pas par période
7
h = T/nbpp;    % pas de calcul
8
n = nbp*nbpp;  % nombre total de pas
Question
Implanter la méthode d'Euler pour résoudre le problème (calculer le vecteur vs_euler contenant les valeurs de la tension de sortie Vs)
Indice
Un copié-collé du fichier précédent devrait fonctionner sans problème pour calculer le courant (i_euler). Il est ensuite facile d'en déduire Vs.
Solution
1
t_euler = zeros(1,n+1);
2
i_euler = zeros(1,n+1);
3
t_euler(1) = t_ini;        
4
i_euler(1) = i0;           
5
for k = 2:n+1                
6
    i_euler(k) = i_euler(k-1) + h*f(t_euler(k-1),i_euler(k-1));
7
    t_euler(k) = t_euler(k-1)+h;
8
end
9
vs_euler = R*i_euler;
Calcul de la tension de sortie avec RK4
On a vu précédemment que la méthode d'Euler était moins précise (à pas de calcul donné) que celle de Runge-Kutta à l'ordre 4, nous allons donc les comparer.
Question
Même question que la précédente pour RK4 en calculant v_RK4.
Solution
1
t_RK4 = zeros(1,n+1);
2
i_RK4 = zeros(1,n+1);
3
t_RK4(1) = t_ini;
4
i_RK4(1) = i0;
5
for k = 2:n+1
6
    f1 = f( t_RK4(k-1) , i_RK4(k-1) ); 
7
    f2 = f( t_RK4(k-1)+h/2 , i_RK4(k-1)+h/2*f1 );
8
    f3 = f( t_RK4(k-1)+h/2 , i_RK4(k-1)+h/2*f2 );
9
    f4 = f( t_RK4(k-1)+h   , i_RK4(k-1)+h*f3 );
10
    i_RK4(k) = i_RK4(k-1) + h/6*(f1+2*f2+2*f3+f4);
11
    t_RK4(k) = t_RK4(k-1)+h;
12
end
13
vs_RK4 = R*i_RK4;
Tracé des résultats
On peut alors tracer VDC, v_euler et v_RK4 sur une même figure :
1
% calcul des valeurs pour tracer VDC
2
nVDC = 10000;  % nombre de points pour le trace
3
t_VDC = t_ini:(t_fin-t_ini)/(nVDC-1):t_fin;
4
% trace des 3 courbes
5
figure(1)
6
plot(t_VDC,VDC(t_VDC),'k-','LineWidth',2)
7
hold on
8
grid on
9
plot(t_euler,vs_euler,'b-','LineWidth',2)
10
plot(t_RK4,vs_RK4,'r-','LineWidth',2)
11
xlabel('Temps (en sec)')                 
12
ylabel('Tension (en V)')                      
13
axis([t_ini, t_fin, 0, round(max(VDC(t_VDC)))+10]) 
14
legend('VDC','Vs (Euler)','Vs (RK4)','Location','SouthEast')
15
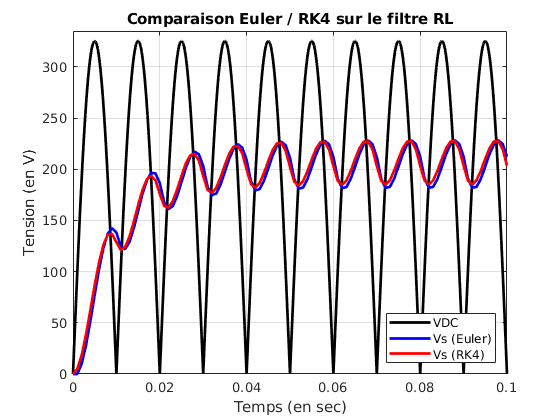
title('Comparaison Euler / RK4 sur le filtre RL')
Et on obtient la figure ci-dessous :
Question
Observer l'influence du pas de calcul sur les résultats pour plusieurs valeurs de la résistance de charge (R = 5, 10, et 20 Ω), ainsi que l'influence de cette dernière sur les oscillations de Vs en régime permanent.