Filtre RLC
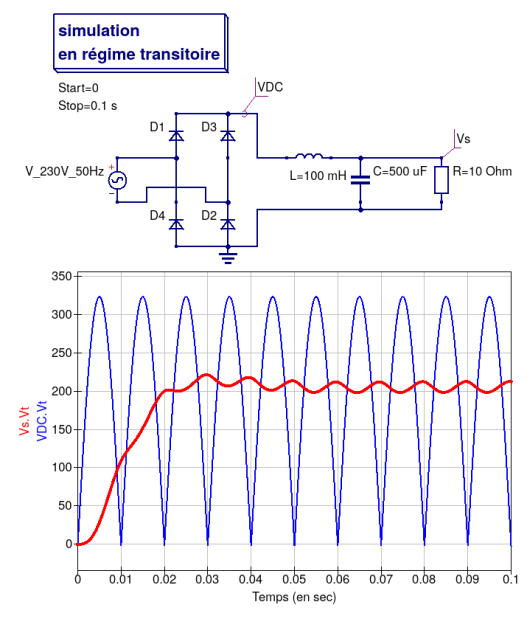
Pour réduire les oscillations de la tension de sortie Vs et leur dépendance à la valeur de la charge, on rajoute souvent une capacité en parallèle de cette dernière. Le montage correspondant est donné ci-dessous :
La seule différence avec celui de la partie précédente est l'ajout d'une capacité de 500 μF en parallèle de R (non chargée à l'instant initial).
Mise en équation
La tension de sortie Vs dépend désormais d'une équation différentielle linéaire d'ordre 2. En effet, en notant \(i\) le courant dans l'inductance et \(i_c\) celui dans le condensateur :
la loi des mailles donne :
\(V_{\text{DC}} = L\,\frac{d\,i}{dt} + V_s\)
et la loi des nœuds donne :
\(i = i_c + \frac{V_s}{R}\)
Or : \(i_c = \frac{d\,q}{dt} = C\,\frac{d\,V_s}{dt}\)
Finalement : \(V_{\text{DC}} = LC\,V_s'' + \frac{L}{R}\,V_s' + V_s\)
On pourrait résoudre en se ramenant à un système du premier ordre de dimension 2 grâce à la même transformation que celle vue dans les modules précédents.
À savoir : \(X = \begin{pmatrix}V_s\\V_s'\end{pmatrix}\).
Mais, en général on préfère utiliser des variables plus « physiquement parlant » : on choisit ce qu'on appelle des variables d'état.
Dans notre cas, on choisira \(i\) et \(V_s\). Ainsi, on obtient :
\(\displaystyle\left\{\begin{array}{l}i'(t) = -\frac{1}{L}\,V_s(t) + \frac{1}{L}\,V_{\text{DC}}(t)\\V_s'(t) = \frac{1}{C}\,i(t) -\frac{1}{RC} V_s(t)\end{array}\right.\), \(~~~i(0) = 0, V_s(0) = 0\)
Question
Mettre le système précédent sous forme matricielle, et modifier le début du fichier FiltreRL.m précédent (après l'avoir renommé en FiltreRLC.m par exemple) pour prendre en compte la nouvelle fonction "f" définissant notre système différentiel.
Solution
% Fichier FiltreRLC.m correspondant au 3eme exercice du TP% Filtre RLC derriere un pont de diodesclear % Nettoyage du Workspace
close all % Fermeture des fenetres restees ouvertes
clc % Nettoyage du terminal de commande
L = 100e-3; % H
R = 10; % Ohm
C = 500e-6; % F
freq = 50; % Hz
w = 2*pi*freq; % s^-1
VDC = @(t) abs(230*sqrt(2)*sin(w*t)); % V
i0 = 0;
Vs0 = 0;
A = [0 -1/L; 1/C -1/(R*C)];
B = @(t) [VDC(t)/L; 0];
f = @(t,X) A*X + B(t);
X0 = [i0;Vs0];
Question
Modifier la suite du programme pour appliquer Euler et RK4 à notre nouveau problème.
Solution
T = 1/freq/2; % periode de la source
nbp = 10; % nombre de periodes pour le calcul
t_ini = 0.; % instant initial
t_fin = nbp*T; % instant final = nbp periodes
nbpp = 10; % nombre de pas par période
h = T/nbpp; % pas de calcul
n = nbp*nbpp; % nombre total de pas
t_euler = zeros(1,n+1);
X_euler = zeros(2,n+1); % attention : 2 coordonnees dans X
t_euler(1) = t_ini;
X_euler(:,1) = X0; % 1ere colonne de X = instant initial
for k = 2:n+1
X_euler(:,k) = X_euler(:,k-1) + h*f(t_euler(k-1),X_euler(:,k-1));
t_euler(k) = t_euler(k-1)+h;
endvs_euler = X_euler(2,:);
t_RK4 = zeros(1,n+1);
X_RK4 = zeros(2,n+1);
t_RK4(1) = t_ini;
X_RK4(:,1) = X0;
for k = 2:n+1
f1 = f( t_RK4(k-1) , X_RK4(:,k-1) );
f2 = f( t_RK4(k-1)+h/2 , X_RK4(:,k-1)+h/2*f1 );
f3 = f( t_RK4(k-1)+h/2 , X_RK4(:,k-1)+h/2*f2 );
f4 = f( t_RK4(k-1)+h , X_RK4(:,k-1)+h*f3 );
X_RK4(:,k) = X_RK4(:,k-1) + h/6*(f1+2*f2+2*f3+f4);
t_RK4(k) = t_RK4(k-1)+h;
endvs_RK4 = X_RK4(2,:);
% calcul des valeurs pour tracer VDCnVDC = 10000; % nombre de points pour le trace
t_VDC = t_ini:(t_fin-t_ini)/(nVDC-1):t_fin;
% trace des 3 courbesfigure(1)
plot(t_VDC,VDC(t_VDC),'k-','LineWidth',2)
hold on
grid on
plot(t_euler,vs_euler,'b-','LineWidth',2)
plot(t_RK4,vs_RK4,'r-','LineWidth',2)
xlabel('Temps (en sec)')
ylabel('Tension (en V)')
axis([t_ini, t_fin, 0, round(max(VDC(t_VDC)))+10])
legend('VDC','Vs (Euler)','Vs (RK4)','Location','SouthEast')
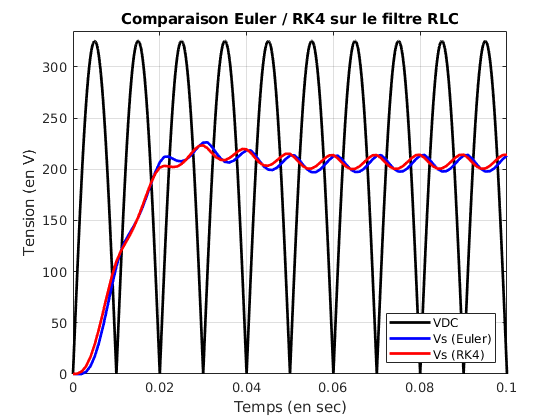
title('Comparaison Euler / RK4 sur le filtre RLC')
Résultats
Question
Observer l'influence du pas de calcul sur les résultats pour plusieurs valeurs de la résistance de charge (R = 5, 10, et 20 Ω), ainsi que l'influence de cette dernière sur les oscillations de Vs en régime permanent. Conclure sur l’intérêt de rajouter une capacité.
Fin du TP, du module et du cours !
J'espère sincèrement que ça vous a plu...
\(\strut\)