Problèmes 3D

Conditions de Jauge sur le potentiel vecteur magnétique

Nous avons déjà vu plusieurs fois précédemment que le potentiel vecteur magnétique ${\bf a}$ était défini à un champ de gradient près et qu’il était donc nécessaire de le jauger pour assurer l’unicité de la solution.

Dans le chapitre précédent, deux méthodes ont été présentées et nous allons maintenant voir leur application à nos problèmes ainsi que la manière de les définir dans GetDP.

Jauge de Coulomb

Par application directe de la méthode du chapitre 2, nous allons définir un champ scalaire $\xi$ dont le gradient permettra d’assurer $\text{div}\,{\bf a} = 0$ en l’introduisant comme multiplicateur de Lagrange dans la formulation.

Ainsi la formulation ccomplète dans le domaine discret sera :

où $W_0^1$ et $W_0^0$ approximent respectivement $\textbf{H}_{0}({\bf rot},\Omega)$ et $\text{H}_{0}({\bf grad},\Omega)$.

Dans GetDP, il faudra d’abord définir ces deux espaces fonctionnels :

Constraint {	
  {Name Dirichlet ;
    Case {      
      { Region Dirichlet ; Type Assign ; Value 0. ; }
    }
  }
}

FunctionSpace {
  { Name Hrot ; Type Form1 ; // W_0^1
    BasisFunction { 
      { Name se ; NameOfCoef ae ; Function BF_Edge ; 
	     Support Region[{Domaine}]  ; Entity EdgesOf[All] ; }  } 
    Constraint {
      { NameOfCoef ae  ; EntityType EdgesOf ; NameOfConstraint Dirichlet ; }
    }
  }  
  { Name Hgrad ; Type Form0 ; // W_0^0
    BasisFunction { 
      { Name sn ; NameOfCoef xin ; Function BF_Node ; 
	       Support Region[{Domaine}]  ; Entity NodesOf[All] ; }  } 
    Constraint {
      { NameOfCoef xin  ; EntityType NodesOf ; NameOfConstraint Dirichlet ; }
    }
  } 
}

Puis la formulation correspondante (exemple pour un problème sans aimants avec lois de comportement magnétiques linéaires) :

Formulation {
  { Name Magnetostat ; Type FemEquation ;
    Quantity {
      { Name a  ; Type Local  ; NameOfSpace Hrot ; }
      { Name xi ; Type Local  ; NameOfSpace Hgrad ; }
    }
    Equation {
      Integral { [ nu[] * Dof{d a} , {d a} ];
	     In Domaine; Jacobian Jvol; Integration Integ; }
      
      Integral { [ -js[] , {a} ];
	     In Bobines; Jacobian Jvol; Integration Integ; }
      
      Integral{ [ Dof{Grad xi} , {a}  ];
	     In Domaine; Jacobian Jvol; Integration Integ; }
      
      Integral { [ Dof{a} , {Grad xi} ];
	     In Domaine; Jacobian Jvol; Integration Integ; }
    }
  } 
}

Le principal inconvénient de cette méthode est d’aboutir à une taille de système conséquente conduisant à des temps de calcul élévés, c’est pourquoi on lui préfèrera généralement la technique suivante.

Jauge d’arbre

Comme vu dans cette partie, nous allons construire un arbre sur l’ensemble des arrêtes du domaine en partant des surfaces sur lesquelles sont imposées des conditions particulières (dans le cas présent, les conditions de Dirichlet) et imposer une circulation nulle de ${\bf a}$ le long de cet arbre directement dans l’espace fonctionnel associé. Ce dernier sera alors noté $W_{0,\text{JA}}^1$, et notre formulation devient ainsi :

La taille du système sera ainsi fortement réduite par rapport au cas précédent puisqu’on s’affranchit du calcul de la grandeur nodale $\xi$.

En pratique, dans GetDP cela se définit de la façon suivante :

Constraint {	
  {Name Dirichlet ;
    Case {      
      { Region Dirichlet ; Type Assign ; Value 0. ; }
    }
  }
  { Name Jauge_arbre ; Type Assign ;
    Case {
      {Region Domaine ; SubRegion Dirichlet ; Value 0. ; }
    }
  }
}

FunctionSpace {
  { Name Hrot ; Type Form1 ;  // W_(0,JA)^1
    BasisFunction { 
      { Name se ; NameOfCoef ae ; Function BF_Edge ; 
	      Support Region[{Domaine}]  ; Entity EdgesOf[All] ; }  } 
    Constraint {
      { NameOfCoef ae  ; EntityType EdgesOf ; NameOfConstraint Dirichlet ; }
      { NameOfCoef ae  ; EntityType EdgesOfTreeIn ; EntitySubType StartingOn ;
	       NameOfConstraint Jauge_arbre ; }
    }
  }  
}

Et la formulation sera strictement la même que dans les cas 2D précédents.

Applications

Retour sur notre inductance pour électronique de puissance

Dans le problème de dimensionnement d’inductance de la page précédente, nous avons utilisé un modèle 2D alors que l’épaisseur de la ferrite utilisée est relativement faible. Il serait donc judicieux de valider (ou non) cette hypothèse par un calcul 3D.

Pour ce faire, je vous fournis le modèle complet (réduit à un huitième de géométrie gràce aux symétries) à Télécharger ici .

Avec, vous pourrez :

• tester les deux types de jauge en linéaire et non-linéaire ;
• observer les valeurs des champs tels que l’induction dans le circuit magnétique par exemple :
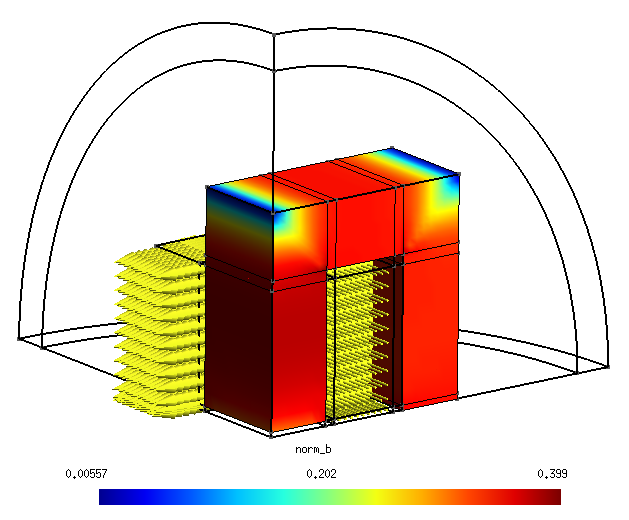
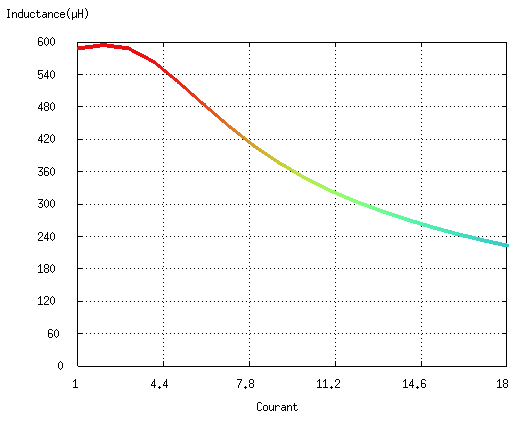
• tester votre design et vérifier si vous respectez le cahier des charges (200 µH sous 15 A) ;
• tracer la valeur de l’inductance en fonction du courant :

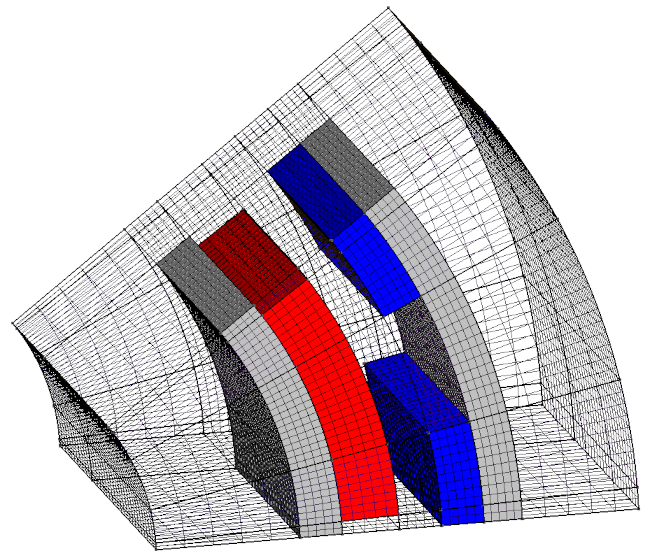
Retour sur notre accouplement à aimants permanents

L’accouplement étudié page précédente reposait lui aussi sur l’hypothèse que les effets de bords sont négligeables et il serait opportun de le vérifier.

Résoudre le problème en 3D et comparer les deux formulations :

1. en potentiel vecteur magnétique (avec la jauge que vous voulez) ;
2. en potentiel scalaire magnétique.

Pour gagner du temps, je vous fournis encore la géométie 3D en cliquant ici . Un exemple de géométrie possible est représenté ci-dessous :