Maillage

Intéressons nous tout d’abords aux éléments géométriques $K$ obtenus par discrétisation du domaine d’étude $\Omega$, ce qu’on appelle le maillage. Le domaine est alors partitionné avec le type d’entités élémentaires choisi (triangle, quadrangle, tétraèdre, hexaèdre, etc…).

Le maillage doit être conforme, c’est-à-dire :

  • Les éléments doivent recouvrir la fermeture $\overline{\Omega}$ de $\Omega$.
  • L’intersection de deux éléments est soit l’ensemble vide, soit un sommet, soit une arête partagée.

Nous pouvons illustrer cela sur un exemple :

Maillage conforme Maillage non conforme
Maillage conforme Maillagenon-conforme

Dans la suite, nous utiliserons le logiciel libre de maillage par éléments finis Gmsh développé par C. Geuzaine et J-F. Remacle.

Génération d’un maillage

Pour pouvoir discrétiser un problème donné, nous devons tout d’abord définir ses aspects purement géométriques. C’est-à-dire créer toutes les entités élémentaires :

  • les points, qui permettent de définir :
  • les lignes (segments, arcs de cercles, voire courbes), qui permettent de définir :
  • les surfaces (planes ou courbes), qui permettent de définir :
  • les volumes.

Sur notre cas d’étude, on obtient par exemple :

Géométrie de notre exemple

Après avoir défini des tailles caractéristiques d’éléments et/ou discrétiser les lignes, on peut mailler notre géométrie. Ci-dessous, deux exemples :

Triangulaire Quadrangulaire
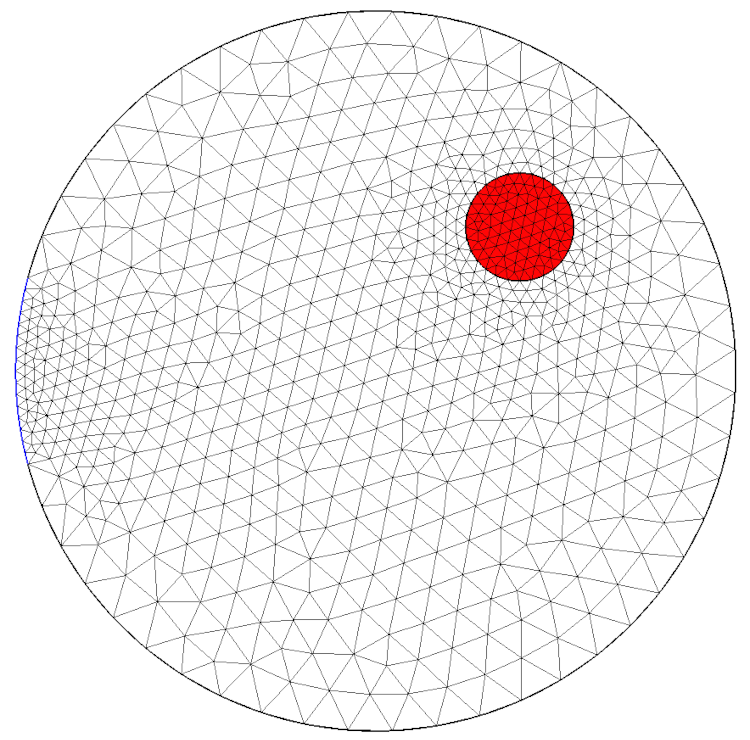
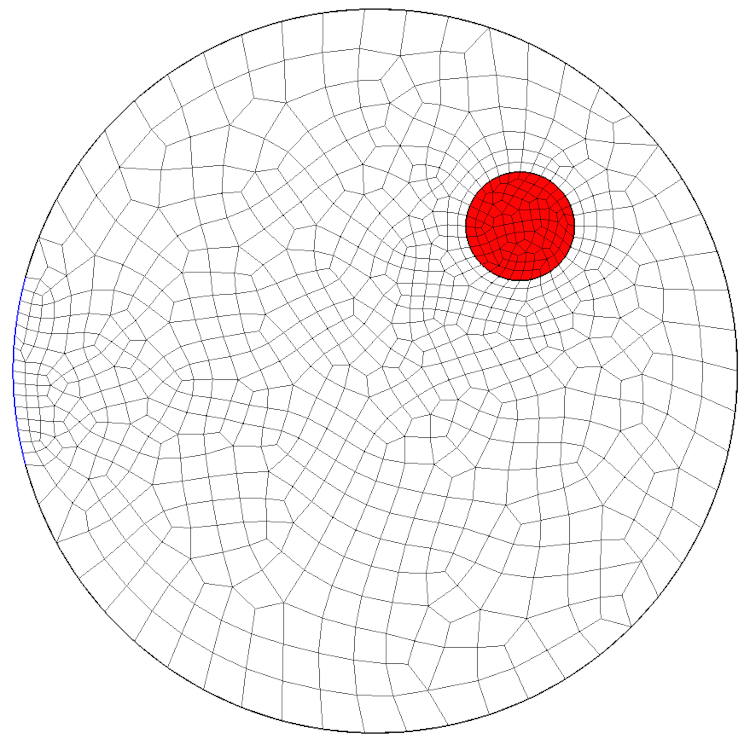
Maillage 1 Maillage 2

Pour information, je vous donne en exemple les scripts permettant de générer ces maillages. Par habitude, j’utilise deux fichiers :

  • data.geo : servant à définir les paramètres qui pourront être partagés avec le solveur,
  • poisson.geo : contenant la création de la géométrie.
/* 
	Fichier data.geo contenant les parametres 
*/

// Parametres geometriques
Rd = 1;
Rs = 0.15*Rd;
xs = 0.4*Rd;  
ys = 0.4*Rd;
alphaN = Pi/6;

// Parametres maillage 
finesse = 2;
nec = 4*finesse;
lcd = Rd/nec;
lcs = Rs/nec*2;
neN = 2*nec;
typele = 1;  // <=1 : triangles
             // > 1 : quadrangles
             
// Numeros regions physiques
DISQUE = 1000;
SOURCE = 1001;
DIRICHLET = 2000;
NEUMANN = 2001;

/*
	Fichier poisson.geo contenant la creation de 
	la geometrie de notre petit probleme de Poisson
*/

// Lecture des parametres
Include "data.geo" ;

// Creation des points
Point(1) = {0,0,0,lcd};  // centre domaine
Point(2) = {Rd/Sqrt[2],Rd/Sqrt[2],0,lcd};
Point(3) = {-Rd*Cos[alphaN/2],Rd*Sin[alphaN/2],0,lcd};
Point(4) = {-Rd*Cos[alphaN/2],-Rd*Sin[alphaN/2],0,lcd};
Point(5) = {Rd/Sqrt[2],-Rd/Sqrt[2],0,lcd};
Point(6) = {xs,ys,0,lcs}; // centre Omega_s
Point(7) = {xs+Rs,ys,0,lcs};
Point(8) = {xs,ys+Rs,0,lcs};
Point(9) = {xs-Rs,ys,0,lcs};
Point(10) = {xs,ys-Rs,0,lcs};

// Creation des lignes
Circle(1) = {2,1,3}; 
Circle(2) = {3,1,4};
Circle(3) = {4,1,5}; 
Circle(4) = {5,1,2};
Circle(5) = {7,6,8}; 
Circle(6) = {8,6,9};
Circle(7) = {9,6,10}; 
Circle(8) = {10,6,7};

// Discretisation de la ligne Gamma_n
Transfinite Line {2}  = neN+1 Using Progression 1.0;

// Surfaces
Line Loop(1) = {1,2,3,4};
Line Loop(2) = {5,6,7,8};
Plane Surface(1) = {2};     // Omega_s
Plane Surface(2) = {1,-2};  // Omega

// Maillage en quadrangles (si voulu)
If (typele > 1)  
  Recombine Surface '*';
EndIf

Physical Surface(DISQUE) = {2};
Physical Surface(SOURCE) = {1};
Physical Line(DIRICHLET) = {1,3,4};
Physical Line(NEUMANN) = {2};

// Un peu de cosmetisme
Color Red { Surface{1}; }
Color White { Surface{2}; }
Color Blue { Line{2};}
Color Black { Line{1,3,4,5,6,7,8};}

En plus des fonctions basiques de création des entités élémentaires, Gmsh possède des fonctions plus évoluées : transformations (symétries, translations, rotations, dilatations), extrusions. De plus, il intègre depuis quelques temps un noyau supplémentaire basé sur le moteur CAO OpenCascade permettant de créer directement des objets 2D ou 3D, d’effectuer des opérations booléennes, ou de manipuler des splines.

Pour plus d’informations sur le logiciel, vous pouvez :
$\rightarrow$ consulter le site officiel et son wiki ;
$\rightarrow$ suivre un très bon tutoriel fait par B. Thierry (ENSEM, promo 2007).

Exemples

Ci-après, vous trouverez des exemples de maillages utilisés dans le cadre de travaux de mon équipe de recherche au laboratoire GREEN.

En 2D

Machine à courant continu Ventouse magnétique
MCC Electromaimant

En 3D

Accouplements magnétiques (maillages structurés) Machines synchrones à griffes (mix structuré / non-structuré)
Coupleur à Aimants Machine Geoffrey
Coupleur à induction Machine Dominique

$~$

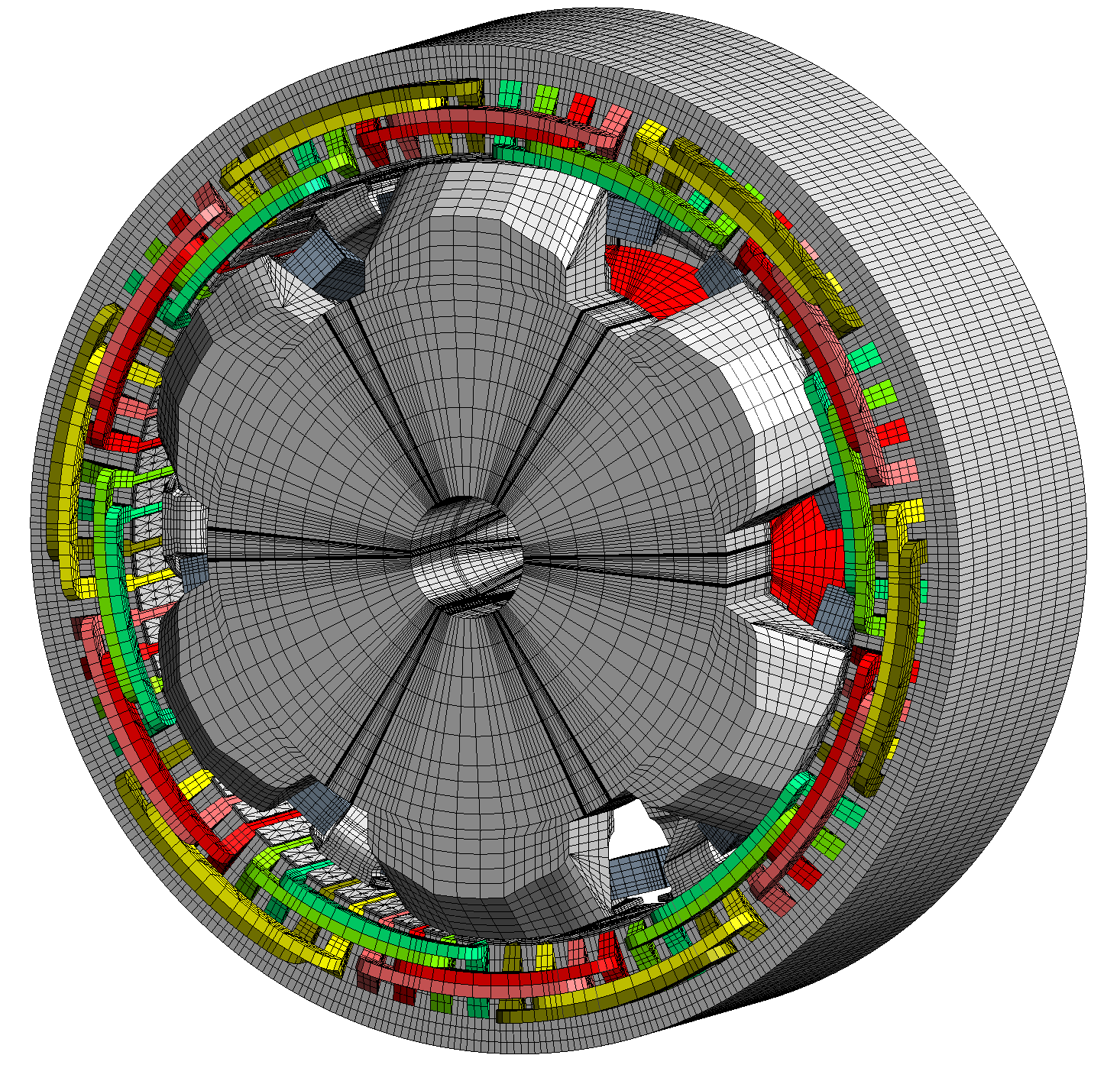
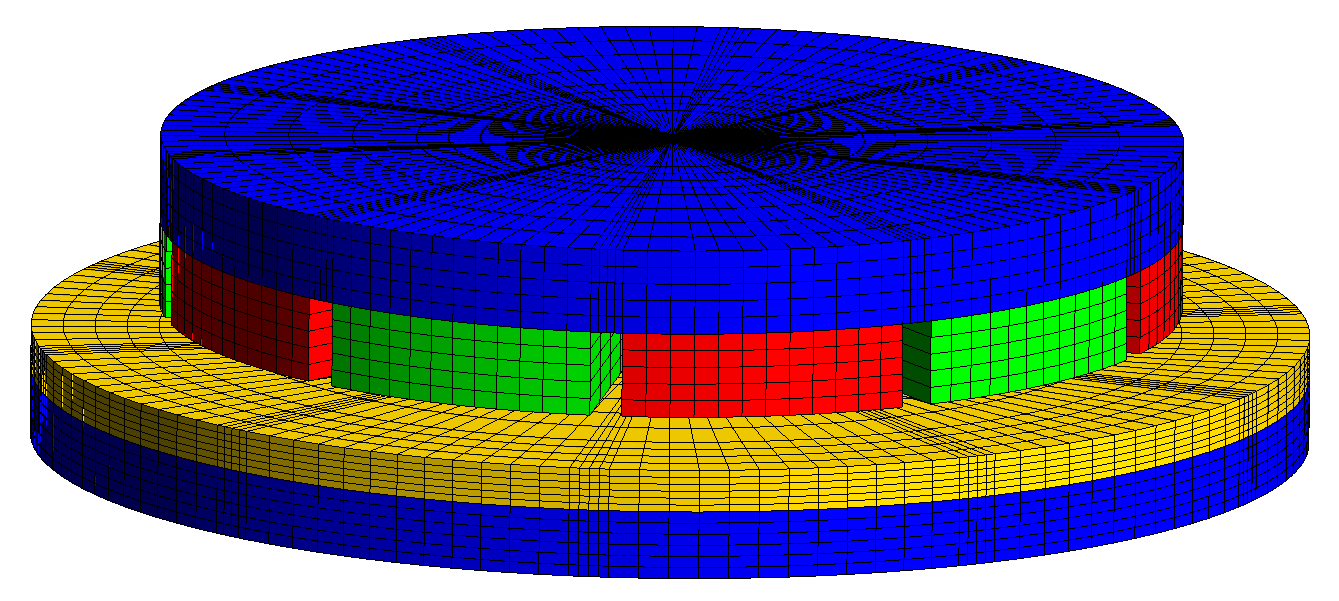
Les exemples ci-dessus sont issus des thèses de :

  • G. Devornique (ENSEM, promo 2013), pour l’alterno-démarreur synchrone à griffes ;
  • B. Ristagno (ENSEM, promo 2016), pour la machine à courant continu ;
  • D. Giraud (ENSEM, promo 2017), pour la machine synchrone axiale à griffes.

Pour plus d’informations, ou si vous envisagez la possibilité de faire une thèse, n’hésitez pas à me contacter, ainsi que mes collègues : les Professeurs N. Takorabet ou D. Netter.

Autres exemples

On peut également utiliser des maillages beaucoup plus complexes, comme par exemple les deux ci-dessous qui me permettent de calculer des courants induits dans des têtes humaines (par exemple pour des travailleurs opérant à proximité de sources basse fréquence comme des pinces à souder) :

John Doe Jane Doe
John Doe Jane Doe