Éléments finis de Whitney
Contexte
Nous venons de développer complètement le principe de la méthode des éléments finis pour des champs scalaires appartenant à $\text{H}^1(\Omega) \left(= \text{H}({\bf grad},\Omega)\right)$. Pour cela, nous avons utilisé des éléments de Lagrange bien adaptés pour ce type d’inconnues.
Cependant les différents champs constituant le champ électromagnétique sont également des grandeurs vectorielles pouvant appartenir à ${\bf H}({\bf rot},\Omega)$ ou ${\bf H}(\text{div},\Omega)$. Typiquement nous ne pouvons résoudre notre formulation rot-rot avec des éléments de Lagrange tels quels. Nous pourrions choisir de résoudre avec trois champs scalaires pour déterminer notre vecteur inconnu (un par composante), mais cette solution est loin d’être la plus pertinente en terme d’efficacité et d’aspects géométriques (respect de certaines conditions de continuité aux interfaces).
Parmi la grande variété d’éléments finis existants, une famille est très largement utilisée pour modéliser des problèmes électromagnétiques : les éléments finis de Whitney. En fait, ces derniers ont été spécifiquement créés dans ce but [Boss93]. Basés sur les formes différentielles du même nom, ils offrent un cadre idéal pour approximer nos champs en 3D car ils permettent de construire de manière séquentielle les espaces discrets auxquels ils appartiennent. Nous allons donc présenter succinctement ces éléments.
Information
En toute rigueur, il faudrait préciser que les éléments de Whitney ne correspondent qu’aux cas particuliers d’élements triangulaires et tétraédriques. Leur généralisation aux autres types d’élements (quadrangles, héxaèdres, prismes, pyramides) rentre dans un cadre plus général appelé éléments de Nédélec.
Éléments de Whitney
Contrairement aux éléments précédents, les éléments de Whitney sont initialement définis en 3D et s’appuient sur des degrés de libertés pouvant être reliés aux valeurs aux nœuds (éléments nodaux), mais aussi aux circulations le long des arêtes (éléments d’arête), aux flux au travers des facettes (éléments de facette), et aux intégrales sur les volumes (éléments de volume) des éléments du maillage. Compte tenu de ces différences de nature entre degrés de liberté, on les appelle parfois éléments finis mixtes.
Astuce
Nous verrons dans la partie applicative qu’il est tout a fait possible de traiter des cas 2D. Selon les cas : soit directement, soit en utilisant certaines adaptations (arêtes ou facettes fictives orthogonales au plan d’étude).
Espaces discrets
Le principe de base est de construire successivement les espaces discrets $W^0$, $W^1$, $W^2$ et $W^3$ permettant d’approximer respectivement $\text{H}({\bf grad},\Omega)$, ${\bf H}({\bf rot},\Omega)$, ${\bf H}(\text{div},\Omega)$ et $L^2(\Omega)$, à partir d’une séquence de fonctions de base, liées respectivement aux nœuds $(\mathcal{N_h})$, aux arêtes $(\mathcal{A_h})$, aux facettes $(\mathcal{F_h})$ et aux volumes $(\mathcal{V_h})$ des éléments du maillage $\mathcal{M_h}$.
On peut synthétiser l’ensemble dans la table suivante :
| Espace | Approxime | Fonctions de bases | Propriété | Degré de liberté | Type d’élément |
|---|---|---|---|---|---|
| $W^0$ | $\text{H}({\bf grad},\Omega)$ | $\{s_n,~ n\in\mathcal{N_h}\}$ | $s_i({\bf x_j}) = \delta_{ij},~$ ${\forall i,j \in\mathcal{N}_h}$ | Valeur nodale | Élément nodal |
| $W^1$ | ${\bf H}({\bf rot},\Omega)$ | $\{ {\bf s_a},~ a\in \mathcal{A_h}\}$ | $\displaystyle \int_j {\bf s_i}\cdot{\bf dl} = \delta_{ij},~$ ${\forall i,j \in\mathcal{A_h}}$ | Circulation le long d’une arête | Élément d’arête |
| $W^2$ | ${\bf H}(\text{div},\Omega)$ | $\{ {\bf s_f},~ f\in \mathcal{F_h}\}$ | $\displaystyle \iint_j {\bf s_i}\cdot{\bf n}~ \text{d}S =\delta_{ij},~$ ${\forall i,j \in\mathcal{F}_h}$ | Flux à travers une face | Élément de facette |
| $W^3$ | $L^2(\Omega)$ | $\{s_v,~ v\in\mathcal{V_h}\}$ | $\displaystyle \iiint_j s_i~\text{d}V = \delta_{ij},~$ ${\forall i,j \in\mathcal{V}_h}$ | Intégrale volumique | Élément de volume |
En procédant ainsi, on respecte la séquence vue sur les espaces continus, à savoir :
$$W^0 \xrightarrow[]{{\bf grad}} W^1 \xrightarrow[]{{\bf rot}} W^2 \xrightarrow[]{\text{div}} W^3 $$Et l’ensemble nous permet également d’assurer les continuités aux interfaces :
- de valeur pour les $s_n$ ;
- de composante tangentielle pour les ${\bf s_a}$ ;
- de composante normale pour les ${\bf s_f}$.
Voyons maintenant comment définir ces fonctions de base (sur les éléments de références).
Fonctions de base
Fonctions de base nodales
Puisque $W_0$ est une approximation de $\text{H}({\bf grad},\Omega) = \text{H}^1$, nous pouvons réutiliser les fonctions définies dans les parties précédentes. Nous aurons donc pour tout nœud $n_i = \{i\}$ de $\mathcal{N_h}$ :
$$s_{n_i} = p_i,~ ~ \forall\,i \in [\![1, n_K]\!]$$Tout ce qui précède reste donc valable. Les fonctions de base nodales des éléments de Whitney sont celles des éléments de Lagrange.
Fonctions de base d’arête
À une arête ${\bf a_{ij}} = \{i\rightarrow j\}$ de $\mathcal{A_h}$, on associe :
$${\bf s_{a_{ij}}} = p_j~{\bf grad}\left(\sum\limits_{r\in \operatorname{N}(j,\overline{i})} p_r \right) - p_i~{\bf grad}\left(\sum\limits_{r\in \operatorname{N}(i,\overline{j})} p_r \right) $$Où $\operatorname{N}(i,\overline{j})$ représente l’ensemble des nœuds de la facette $f$ contenant le nœud $i$ mais pas le nœud $j$.
Remarque : Dans le cas du tétraèdre, l’expression ci-dessus se ramène à :
$${\bf s_{a_{ij}}} = p_i~{\bf grad}\,p_j - p_j~{\bf grad}\,p_i$$À titre d’illustration, nous traçons un exemple pour les triangle, quadrangle, tétraèdre et hexaèdre de référence ci-dessous :
| ${\bf s_{a_{23}}}$ sur tétraèdre | ${\bf s_{a_{23}}}$ sur hexaèdre |
|---|---|
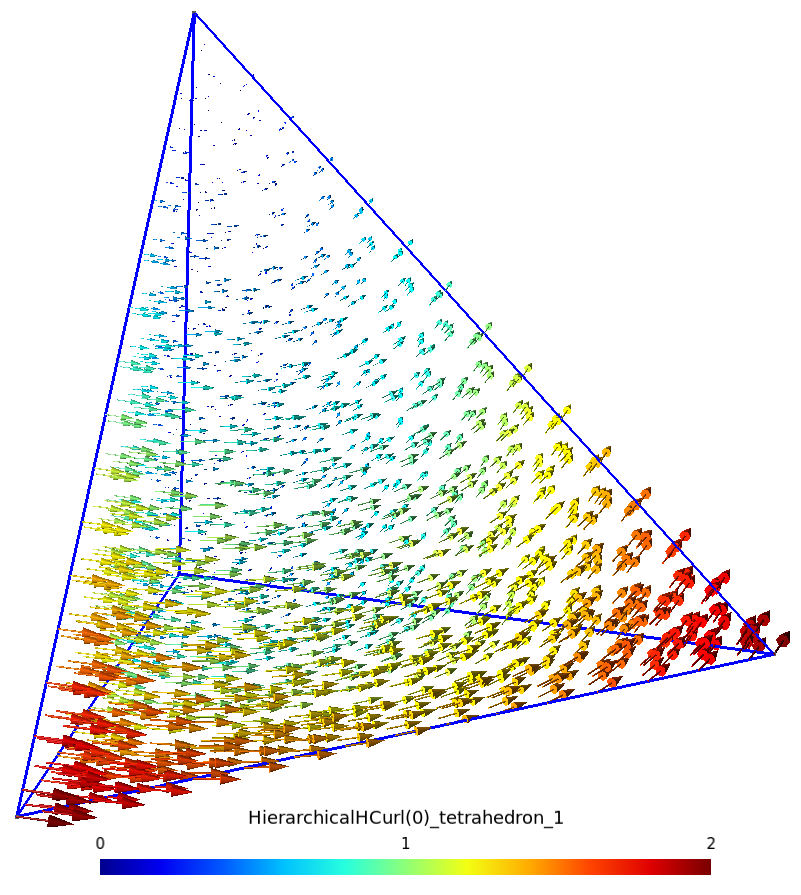
 |
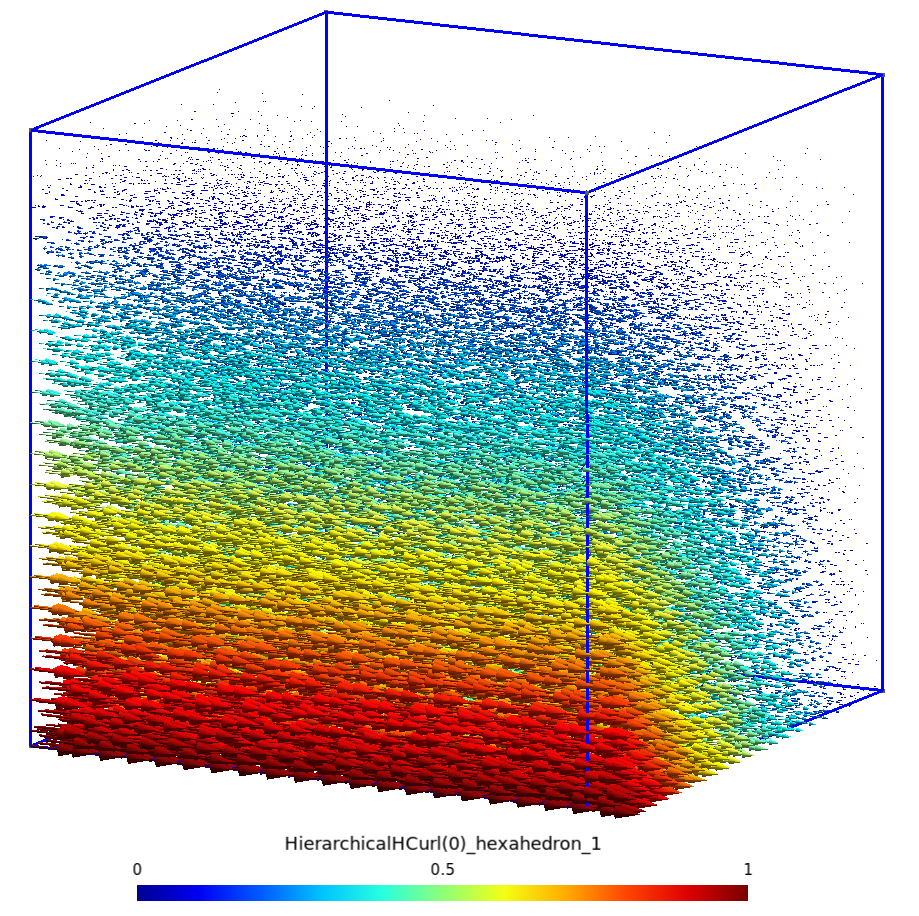
 |
En considérant une facette fictive $f$ orthogonale au plan d’étude, on peut définir nos fonctions de base en 2D, et dans ce cas, on obtient :
| ${\bf s_{a_{23}}}$ sur triangle | ${\bf s_{a_{23}}}$ sur quadrangle |
|---|---|
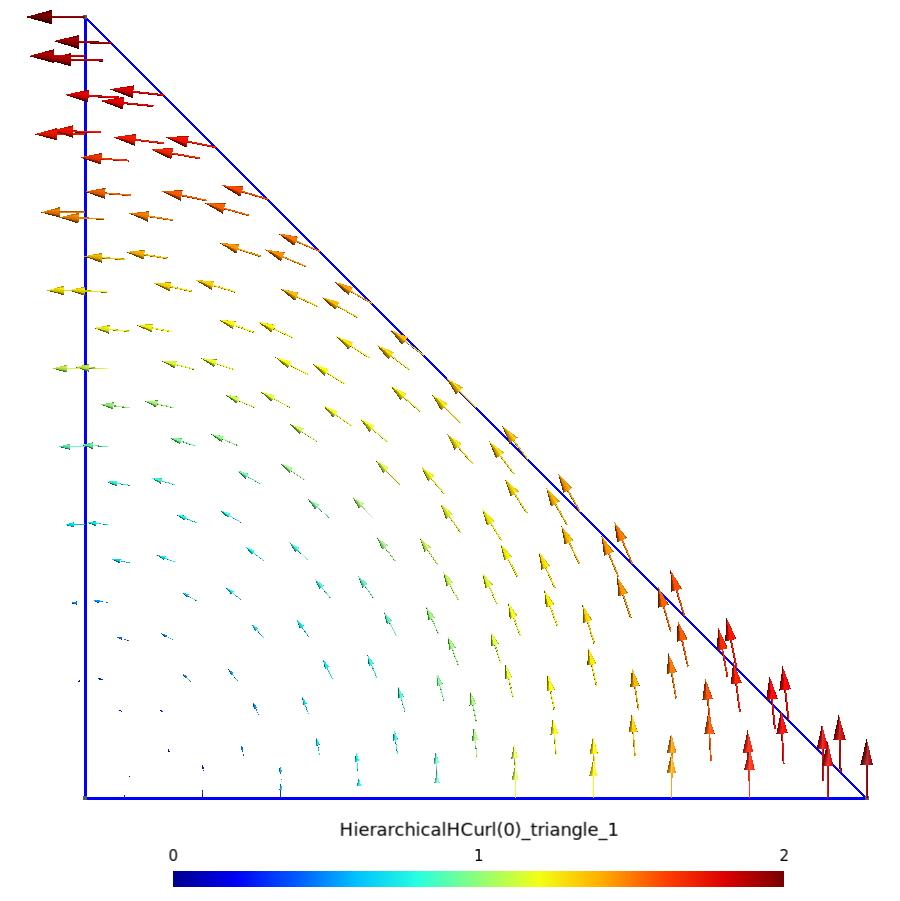
 |
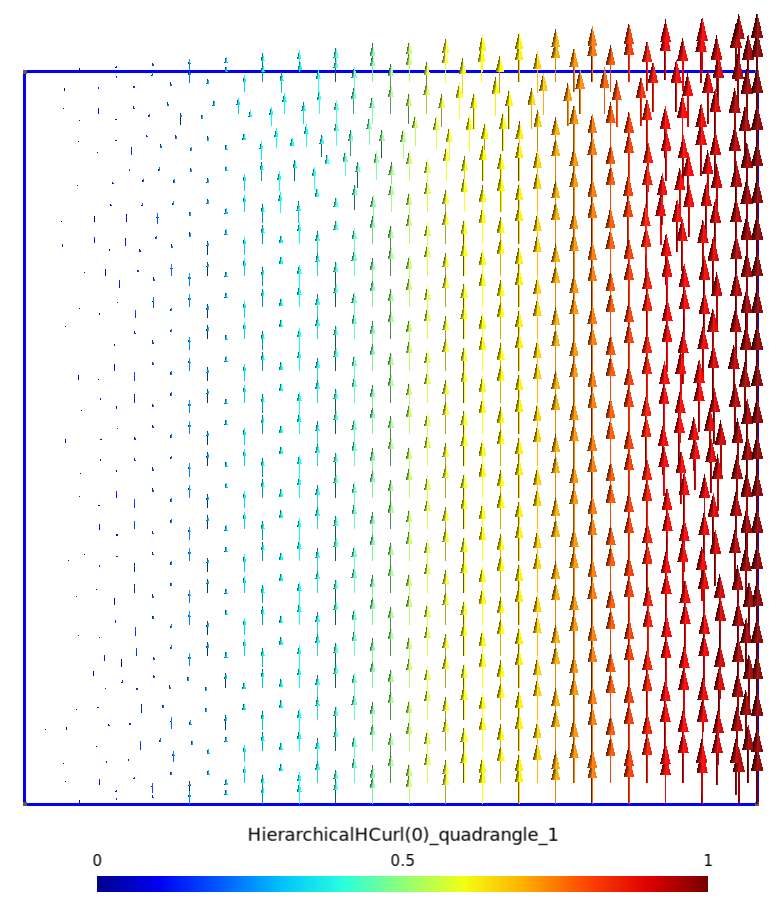
 |
Fonctions de base de facette
À une facette orientée ${\bf f_{ijk}} = \{i,j,k\} = \operatorname{N}({\bf f_{ijk}})$ (si tétrahèdre) ou ${\bf f_{ijkl}} = \{i,j,k,l\} = \operatorname{N}({\bf f_{ijkl}})$ (si hexaèdre) de $\mathcal{F_h}$, on associe :
$${\bf s_{f_{ijk(l)}}} = a~{\large \sum\limits_{q \in \operatorname{N}({\bf f_{ijk(l)}})}} { p_q \left({\bf grad}\,\sum\limits_{r \in \operatorname{N}(q,\overline{q+1})} p_r \right)\wedge\left({\bf grad}\,\sum\limits_{r \in \operatorname{N}(q,\overline{q-1})} p_r \right) }$$où la liste des nœuds de la facette $\operatorname{N}({\bf f})$ est rendue circulaire, $\operatorname{N}(i,\overline{j})$ conserve sa définition précédente et $a$ est un coefficient tel que : $ a= 2$ si $\dim(\operatorname{N}({\bf f})) = 3$ et $a = 1$ si $\dim(\operatorname{N}({\bf f})) = 4$.
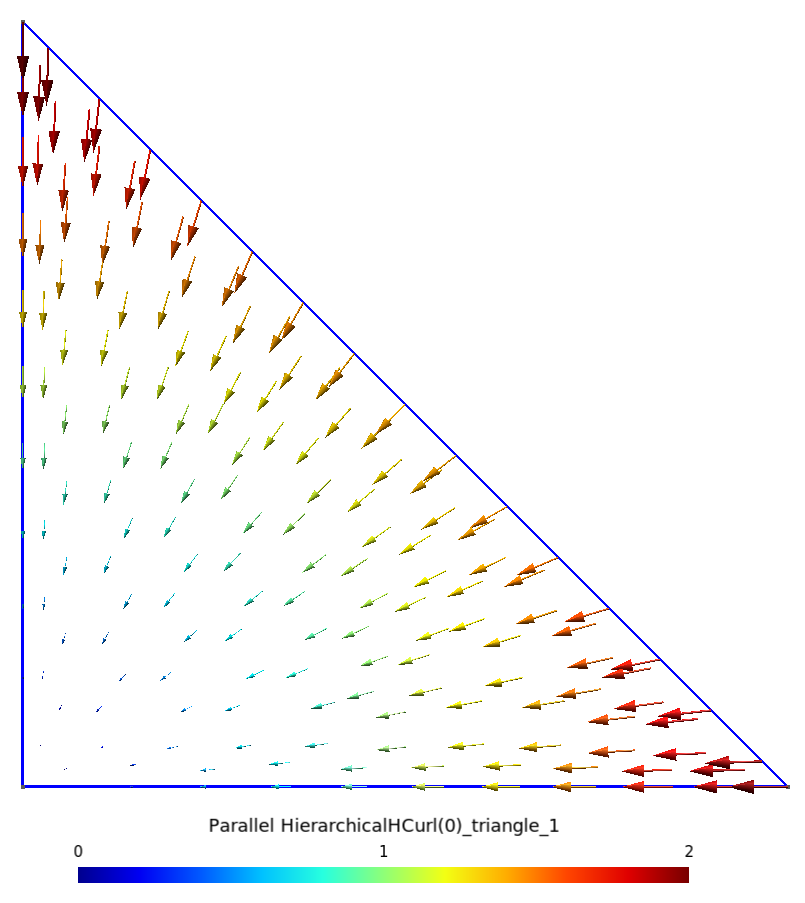
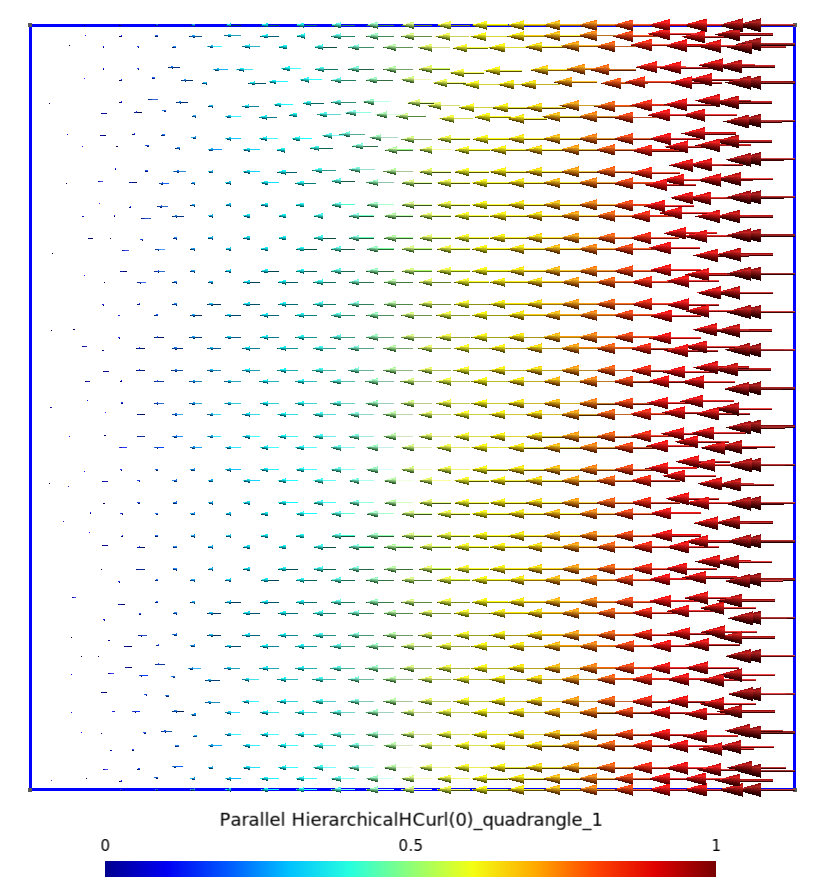
On représente graphiquement ces fonctions de facette en 2D (facette fictive perpendiculaire au plan d’étude) dans la table ci-dessous :
| ${\bf s_{f_{23\perp}}}$ sur triangle | ${\bf s_{f_{23\perp}}}$ sur quadrangle |
|---|---|
 |
 |
Fonctions de base de volume
À l’élément $K$, on fait correspondre la fonction de base de volume :
$$s_{v_K} = \frac{1}{\operatorname{vol}(K)}$$qui est donc constante sur l’élément.
Remarque
Degrés de liberté
Avec les définitions précédentes on peut décomposer tout champ scalaire ou vectoriel selon son espace d’appartenance :
-
Soit $u \in \text{H}({\bf grad},\Omega)$, son approximation sur $\mathcal{M_h}$ est $u_h \in W^0$ tel que :
$$u_h = \sum\limits_{n\in\mathcal{N_h}} \sigma_n(u_h)\,s_n = \sum\limits_{n\in\mathcal{N_h}} u_n\,s_n$$avec :
$$u_n = u_h({\bf x_n})$$ -
Soit ${\bf u} \in \textbf{H}({\bf rot},\Omega)$, son approximation sur $\mathcal{M_h}$ est ${\bf u_h} \in W^1$ tel que :
$${\bf u_h} = \sum\limits_{a\in\mathcal{A_h}} \sigma_a({\bf u_h})\,{\bf s_a} = \sum\limits_{a\in\mathcal{A_h}} {u_a}\,{\bf s_a}$$avec :
$$u_a = \int_a {\bf u_h}\cdot{\bf dl}$$ -
Soit ${\bf u} \in \textbf{H}(\text{div},\Omega)$, son approximation sur $\mathcal{M_h}$ est ${\bf u_h} \in W^2$ tel que :
$${\bf u_h} = \sum\limits_{f\in\mathcal{F_h}} \sigma_f({\bf u_h})\,{\bf s_f} = \sum\limits_{f\in\mathcal{F_h}} {u_f}\,{\bf s_f}$$avec :
$$u_f = \iint_f {\bf u_h}\cdot{\bf n}~\text{d}S$$ -
Soit $u \in L^2(\Omega)$, son approximation sur $\mathcal{M_h}$ est $u_h \in W^3$ tel que:
$$u_h = \sum\limits_{v\in\mathcal{V_h}} \sigma_v(u_h)\,s_v = \sum\limits_{v\in\mathcal{V_h}} u_v\,s_v$$avec :
$$u_v = \iiint_v u_h~\text{d}V$$
Ainsi, en décomposant nos approximations dans les bons espaces, on peut appliquer la méthode de Galerkin en utilisant les fonctions de base ci-dessus comme fonctions tests. Par analogie avec les éléments nodaux de la section précédente, on se ramènera donc à la résolution d’un système linaire où le vecteur inconnu ${\bf U_h}$ correspondra aux différents degrés de liberté.
Application des éléments d’arête à la formulation rot-rot
Formulation
On rappelle la formulation faible continue à résoudre :
$$\left\{\begin{aligned}&\text{Trouver}~ {\bf u} \in\textbf{H}_0({\bf rot},\Omega) ~ \text{tel que :} \\ & \left(\alpha\,{\bf rot\,u},{\bf rot\,v}\right)_{\Omega} = - \left(\boldsymbol{\beta},{\bf v}\right)_{\Omega} - \left<\alpha\,\boldsymbol{\gamma},{\bf v}\right>_{\Gamma_n},~ \forall\,{\bf v} \in \textbf{H}_0({\bf rot},\Omega) \end{aligned}\right.$$Qui devient en discret :
$$\left\{\begin{aligned}&\text{Trouver}~ {\bf u_h} \in W_0^1 ~ \text{tel que :} \\ & \left(\alpha\,{\bf rot\,u_h},{\bf rot\,v_h}\right)_{\Omega} + \left(\boldsymbol{\beta},{\bf v_h}\right)_{\Omega} + \left<\alpha\,\boldsymbol{\gamma},{\bf v_h}\right>_{\Gamma_n} = 0,~ \forall\,{\bf v_h} \in W_0^1\end{aligned}\right.$$Où $W_0^1 \in W^1$ est obtenu en annulant les degrés de liberté sur les arêtes appartenant à la frontière $\Gamma_d$. On constate que cela implique bien notre condition de bord :
$$\left.{\bf u_h}\wedge{\bf n}\right|_{\Gamma_d} = {\bf 0}~ , ~ \text{sur}~ \Gamma_d$$La façon de procéder est identique à celle basée sur les éléments nodaux. Nous pouvons calculer les contributions de chaque arête élément par élément et les ajouter à la matrice de raideur globale ${\bf A_h}$, ou au vecteur second membre ${\bf B_h}$. On peut finalement résoudre le système obtenu, mais seulement après avoir implanté une condition de jauge comme expliqué ci-après. En effet, une telle formulation sous forme brute conduit à une matrice ${\bf A_h}$ singulière.
Condition de jauge
Nous savons malheureusement qu’un problème général (en 3D) comme celui-ci n’a pas de solution unique (vient de l’équivalence avec la formulation forte) et que le champ ${\bf u_h}$ solution est défini à un champ de gradient près. Il est alors impossible de résoudre le système obtenu sans avoir ajouté de condition de jauge particulière. Nous allons donc voir comment procéder.
Jauge d’arbre
Dans le domaine continu, pour rendre ${\bf u}$ unique, on peut ajouter une condition du type :
$${\bf u}\cdot{\bf w} = 0$$Où ${\bf w}$ est un champ de vecteurs dont les lignes de champ ne sont pas fermées et sont telles qu’elles peuvent relier toute paire de points quelconque du domaine d’étude $\Omega$ (par exemple un champ de gradient divergeant).
Dans le domaine discret, nous allons construire un arbre. C’est un ensemble d’arêtes qui relient tous les nœuds du maillage entre eux sans former de chemin fermé. Les arêtes du maillage qui ne sont pas dans l’arbre constituent le co-arbre associé. Un moyen de jauger ${\bf u_h}$ est ainsi d’annuler les composantes sur les arrêtes de l’arbre (condition équivalente à celle continue ci-dessus). Afin de ne pas dénaturer les conditions imposées sur $\Gamma_d$, il convient de commencer à construire l’arbre à partir des arrêtes de cette frontière. Une représentation graphique est donnée ci-dessous :

Exemple d'un arbre (trait bleu) et d'un co-arbre (trait noir) sur des éléments 3D. Les nœuds sont en rouge et la partie grisée appartient à $\Gamma_d$
En rajoutant la condition de jauge d’arbre dans l’espace fonctionnel auquel appartient ${\bf u_h}$ (que nous noterons $W_{0,\text{JA}}^1 \subset W_0^1$), nous pouvons alors résoudre notre formulation faible rot-rot qui s’exprime :
$$\boxed{\left\{\begin{aligned}&\text{Trouver}~ {\bf u_h} \in W_{0,\text{JA}}^1 ~ \text{tel que :} \\ & \left(\alpha\,{\bf rot\,u_h},{\bf rot\,v_h}\right)_{\Omega} + \left(\boldsymbol{\beta},{\bf v_h}\right)_{\Omega} + \left<\alpha\,\boldsymbol{\gamma},{\bf v_h}\right>_{\Gamma_n} = 0,~ \forall\,{\bf v_h} \in W_{0,\text{JA}}^1\end{aligned}\right.}$$Cette façon de procéder est la plus efficace d’un point de vue numérique car elle permet de réduire la taille du système à résoudre (par annulation des degrés de liberté liés au arêtes de l’arbre). Cependant la solution obtenue perd son sens physique, seul son rotationnel pourra être interprété physiquement. Pour de plus amples compléments, je vous renvoie à [Dula94] .
Jauge de Coulomb
Une autre Jauge possible est d’annuler la divergence de notre inconnue (Jauge de Coulomb) :
$$\text{div}\,{\bf u} = 0$$Pour obtenir la forme faible de cette condition, considérons un champ scalaire $\mu$ quelconque de $\text{H}({\bf grad},\Omega)$. On a :
$$\iiint_{\Omega}\text{div}({\bf u})\,\mu ~\text{d}V = 0$$En utilisant la formule de Green en grad-div :
$$\iiint_{\Omega} {\bf u}\cdot{\bf grad}\,\mu ~ \text{d}V - \iiint_{\Omega} \text{div}(\mu\,{\bf u})~ \text{d}V =0$$En appliquant le théorème de la divergence et en séparant les deux frontières :
$$\iiint_{\Omega} {\bf u}\cdot{\bf grad}\,\mu ~ \text{d}V - \iint_{\Gamma_d} \mu\,{\bf u}\cdot{\bf n}~ \text{d}S - \iint_{\Gamma_n} \mu\,{\bf u}\cdot{\bf n} ~ \text{d}V =0$$Nous ne considérerons que le cas d’une condition de Neumann homogène sur $\Gamma_n$ $(\boldsymbol{\gamma} = 0)$, soit : $\left.{\bf rot\,u}\wedge{\bf n}\right|_{\Gamma_n} = 0$. On peut donc en déduire : $\left.{\bf u}\cdot{\bf n}\right|_{\Gamma_n} = 0$. En choisissant $\mu = 0$ sur $\Gamma_d$, on annule le second terme surfacique.
Ainsi, notre condition de Jauge est équivalente à :
$$\boxed{\iiint_{\Omega} {\bf u}\cdot{\bf grad}\,\mu ~ \text{d}V = 0~ ,~ ~ \forall \, \mu \in \text{H}_0({\bf grad},\Omega)}$$Si nous ajoutons uniquement ce terme à la formulation faible initiale, nous nous trouverons face à une formulation avec une fonction inconnue et deux fonctions tests. Pour remédier à cela, nous devons introduire un multiplicateur de Lagrange $\lambda$. Ainsi la formulation variationnelle complète devient :
$$\left\{\begin{aligned}&\text{Trouver}~ {\bf u} \in\textbf{H}_0({\bf rot},\Omega),~ \lambda \in \text{H}_0({\bf grad},\Omega) ~ \text{tels que :} \\ &\left(\alpha\,{\bf rot\,u},{\bf rot\,v}\right)_{\Omega} + \left({\bf grad}\,\lambda,{\bf v}\right)_{\Omega} + \left(\boldsymbol{\beta},{\bf v}\right)_{\Omega} = 0,~ \forall\,{\bf v} \in \textbf{H}_0({\bf rot},\Omega)\\ &\left({\bf u},{\bf grad}\,\mu\right)_{\Omega} = 0, \forall \, \mu \in \text{H}_0({\bf grad},\Omega)\end{aligned}\right.$$La transcription dans le domaine discret est immédiate :
$$\boxed{\left\{\begin{aligned}&\text{Trouver}~ {\bf u_h} \in W_0^1,~ \lambda_h \in W_0^0~ \text{tels que :} \\ &\left(\alpha\,{\bf rot\,u_h},{\bf rot\,v_h}\right)_{\Omega} + \left({\bf grad}\,\lambda_h,{\bf v_h}\right)_{\Omega} + \left(\boldsymbol{\beta},{\bf v_h}\right)_{\Omega} = 0,~ \forall\,{\bf v_h} \in W_0^1 \\ &\left({\bf u_h},{\bf grad}\,\mu_h\right)_{\Omega} = 0, \forall \, \mu_h \in W_0^0 \end{aligned}\right.}$$Cette façon de procéder est plus lourde à résoudre : le système est beaucoup plus grand que le précédent car on a rajouté autant de degrés de liberté que de nœuds du maillage. Cependant, elle a le mérite de fournir une solution « plus physique » et plus facilement interprétable.