Magnétoharmonique

Dans le cas particulier où les sources sont en régime sinusoïdal forcé de pulsation $\omega$, nous pourrons utiliser la transformation complexe vue dans le chapitre 1 et résoudre directement en complexe : c’est ce qu’on appelle la magnétoharmonique (certains l’appellent « magnétostatique complexe »).

La formulation faible à résoudre est alors :

Trouver $\underline{\bf a} \in \textbf{H}_{0}({\bf rot},\Omega) = \{ \underline{\bf a} \in \textbf{H}({\bf rot},\Omega) : \underline{\bf a}\wedge{\bf n}|_{\Gamma_{d}} = 0\}$ et $\underline{v} \in \text{H}_{0}({\bf grad},\Omega) = \{ \underline{u} \in \text{H}({\bf grad},\Omega) : \underline{u}|_{\Gamma_{di}} = \underline{v_i}\}$, tels que :

$$\left\{\begin{aligned}\left(\mu^{-1}\,{\bf rot}\,\underline{\bf a}\,,\,{\bf rot}\,\underline{\bf a'}\right)_{\Omega} + \left(\sigma\,j\omega\,\underline{\bf a}\,,\,\underline{\bf a'}\right)_{\Omega_c} + \left( \sigma\,{\bf grad}\,\underline{v} \,,\, \underline{\bf a'}\right)_{\Omega_c} = 0,~ ~ \forall\,\underline{\bf a'} \in \textbf{H}_{0}({\bf rot},\Omega) \\ (\sigma\,{\bf grad}\,\underline{v} \,,\, {\bf grad}\,\underline{v'})_{\Omega_c} + (\sigma\,j\omega\,\underline{\bf a} \,,\, {\bf grad}\,\underline{v'})_{\Omega_c} = 0,~ ~ \forall\, \underline{v'} \in \text{H}_{0}({\bf grad},\Omega)\end{aligned}\right.$$

L’implantation dans GetDP n’est pas plus compliquée que ce que nous avons vu jusqu’à présent. Le passage en complexe et la fréquence associée sont précisés dans la partie « Résolution » :

Resolution {
  { Name MagnetoHarmonique_2D;
    System {
      { Name A; NameOfFormulation MagnetoHarmonique_2D;
			Type ComplexValue; Frequency freq;
      }
    }
    Operation {
      Generate[A];
      Solve[A]; 
      SaveSolution[A];
    }
  }
}

Et la multiplication par $j\omega$ dans la formulation peut-être faite (au choix) :

directement via un terme Complex[0,1]*2*Pi*freq dans les expressions ;
ou en utilisant DtDof qui permet de définir une dérivée temporelle des degrés de liberté.

Applications

Barre cylindrique

À titre d’exemple, je vous propose de résoudre numériquement l’exercice sur la barre cylindre alimentée en alternatif.

Le modèle est téléchargeable ici .

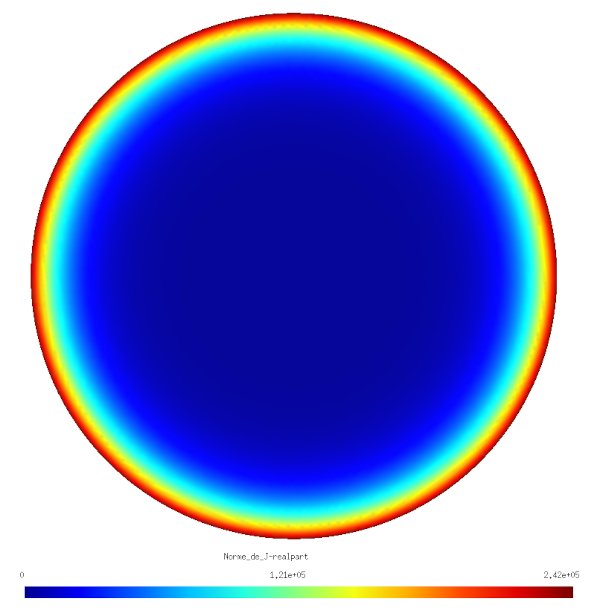
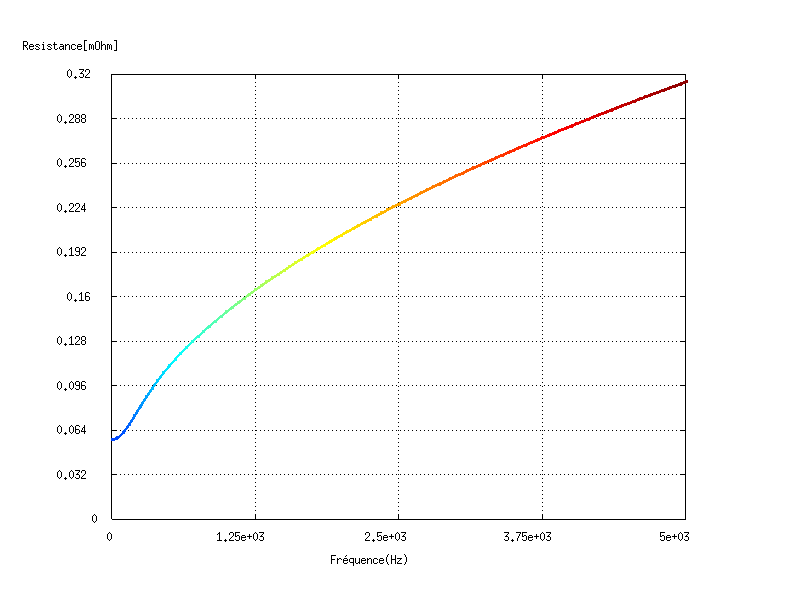
Observer l’effet de peau ainsi que l’évolution de la résistance du conducteur en fonction de la fréquence :

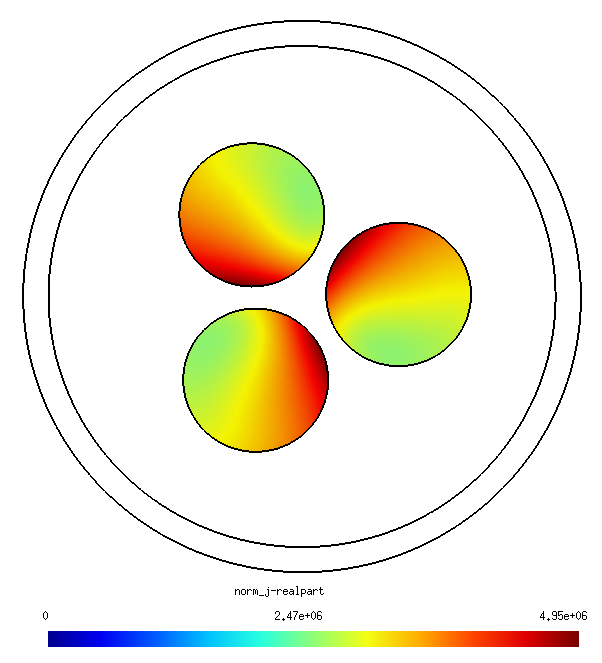
Câble triphasé

Modifier les programmes précédents afin de modéliser une ligne triphasée et observer l’effet de proximité à 50 Hz :