Fonctions de base sur éléments nodaux
Maintenant que nous savons créer le maillage (noté $\mathcal{M}_h$), nous allons nous intéresser à la définition des fonctions qui permettront de constituer la base de l’approximation discrète $V_h$ de $V$ (fonctions de base).
Remarque
Par souci de simplicité, nous ne nous intéresserons, dans un premier temps, qu’aux éléments nodaux permettant d’approximer $\text{H}^1_0(\Omega) \left(= \text{H}_0({\bf grad},\Omega)\right).$ On les appelle éléments de Lagrange. Pour clarifier un peu plus les choses, nous ne considérerons tout d’abord que des éléments s’appuyant sur des fonctions de base linéaires (polynômes d’ordre 1) permettant une approximation linéaire par morceaux de la fonction inconnue. On les appelle les éléments $\mathbf{P_1}$ (ou $\mathbf{Q_1}$ pour les quadrangles).
Éléments de référence
En fait, nous allons définir les fonctions de base sur ce qu’on appelle un élément de référence dont la forme géométrique est fixe et prédéfinie.
En 1D
En dimension 1, les éléments sont des segments et l’élément de référence est le segment $[-1,1]$.
En 2D
En dimension 2, nous pouvons donner le triangle et le quadrangle de référence :
- pour le triangle, c’est celui de sommets : ${\bf n_1}=(0,0)$, ${\bf n_2}=(1,0)$ et ${\bf n_3} = (0,1)$. On peut le paramétrer par : $$\Delta_r = \left\{ (u,v) \in \mathbb{R}^2 : 0 \le u \le 1, 0 \le v\le 1-u\right\}$$
- pour le quadrangle, c’est celui de sommets : ${\bf n_1} = (-1,-1)$, ${\bf n_2} = (1,-1)$, ${\bf n_3} = (1,1)$ et ${{\bf n_4} =(-1,1)}$. On peut le paramétrer par : $$\text{Q}_r = \left\{ (u,v) \in \mathbb{R}^2 : -1 \le u \le 1, -1 \le v \le 1\right\}$$
Leur représentation graphique est donnée ci-dessous.

Éléments de référence en 2D
En 3D
Nous nous contenterons de donner le tétraèdre et l’hexaèdre de référence :
- pour le tétraèdre, c’est celui de sommets : ${\bf n_1} = (0,0,0)$, ${\bf n_2} = (1,0,0)$, ${\bf n_3} = (0,1,0)$ et ${{\bf n_4} =(0,0,1)}$. On peut le paramétrer par : $$\text{T}_r = \left\{ (u,v,w) \in \mathbb{R}^3 : 0 \le u \le 1, 0 \le v\le 1-u, 0 \le w\le 1-u-v\right\}$$
- pour l’hexaèdre, c’est celui de sommets : ${\bf n_1} = (-1,-1,-1)$, ${\bf n_2} = (1,-1,-1)$, ${\bf n_3} = (1,1,-1)$, ${\bf n_4} = (-1,1,-1)$, ${\bf n_5} = (-1,-1,1)$, ${\bf n_6} = (1,-1,1)$, ${\bf n_7} = (1,1,1)$ et ${\bf n_8} = (-1,1,1)$. On peut le paramétrer par : $$\text{H}_r = \left\{ (u,v,w) \in \mathbb{R}^3 : -1 \le u \le 1, -1 \le v \le 1, -1 \le w \le 1\right\}$$
Et leur représentation graphique est donnée ci-dessous.

Éléments de référence en 3D
Fonctions de base sur éléments de référence
Sur ces élément de références, nous pouvons définir des fonctions linéaires valant 1 sur un sommet (un nœud) et 0 sur les autres. Dans ce cas, on fera une approximation linéaire par morceaux de notre fonction inconnue. Ces fonctions seront notées $p_i$ pour $i \in [\![1,n_K]\!]$.
Nous aurons donc autant de fonctions de base que de sommets $n_K$ de l’élément de référence.
Cas du triangle
Dans le cas du triangle de référence, ces fonctions sont données par la table ci-dessous :
| Nœud $i$ | Fonction de base $p_i (u,v)$ |
|---|---|
| 1 | $p_1 (u,v) = 1 - u - v$ |
| 2 | $p_2 (u,v) = u$ |
| 3 | $p_3 (u,v) = v$ |
Une représentation graphique est donnée par :

On peut également les tracer en surélevé :
| $p_1$ | $p_2$ | $p_3$ |
|---|---|---|
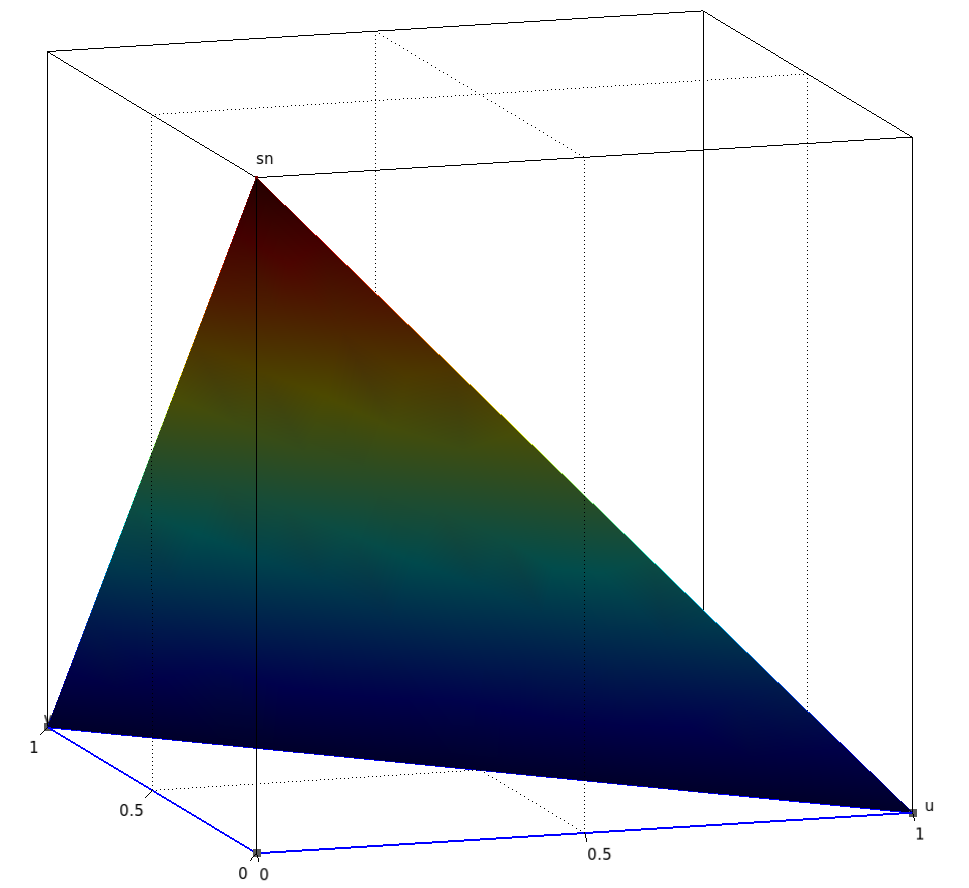
 |
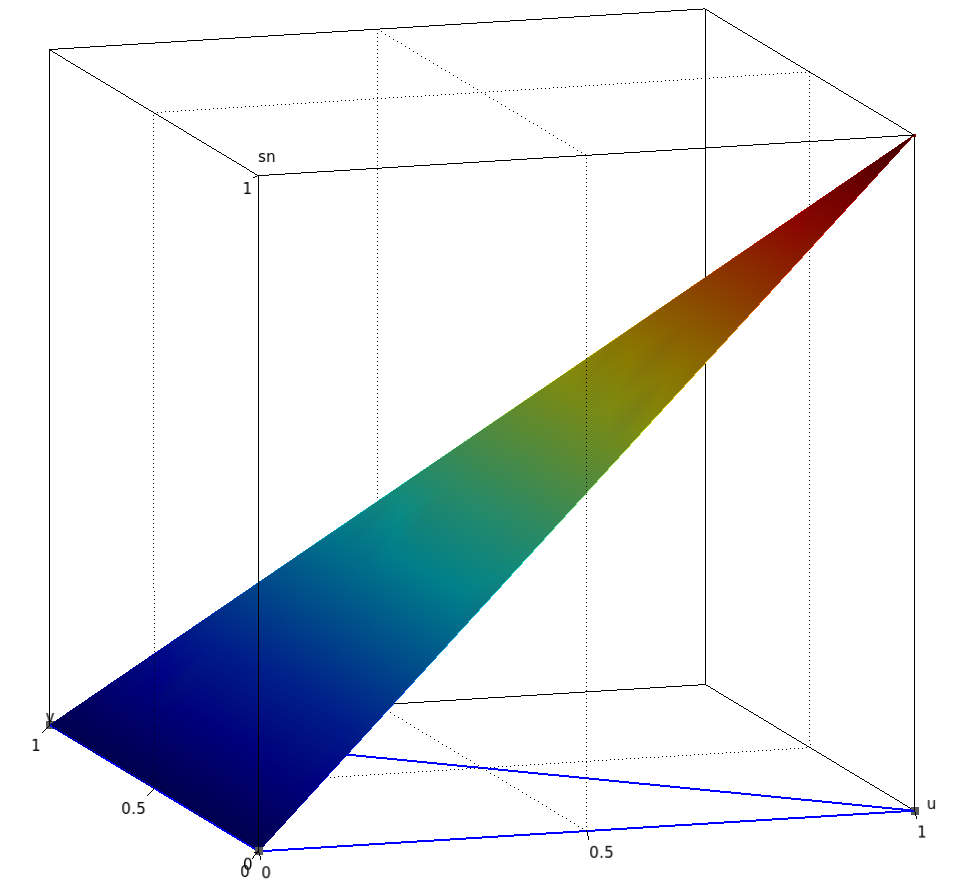
 |
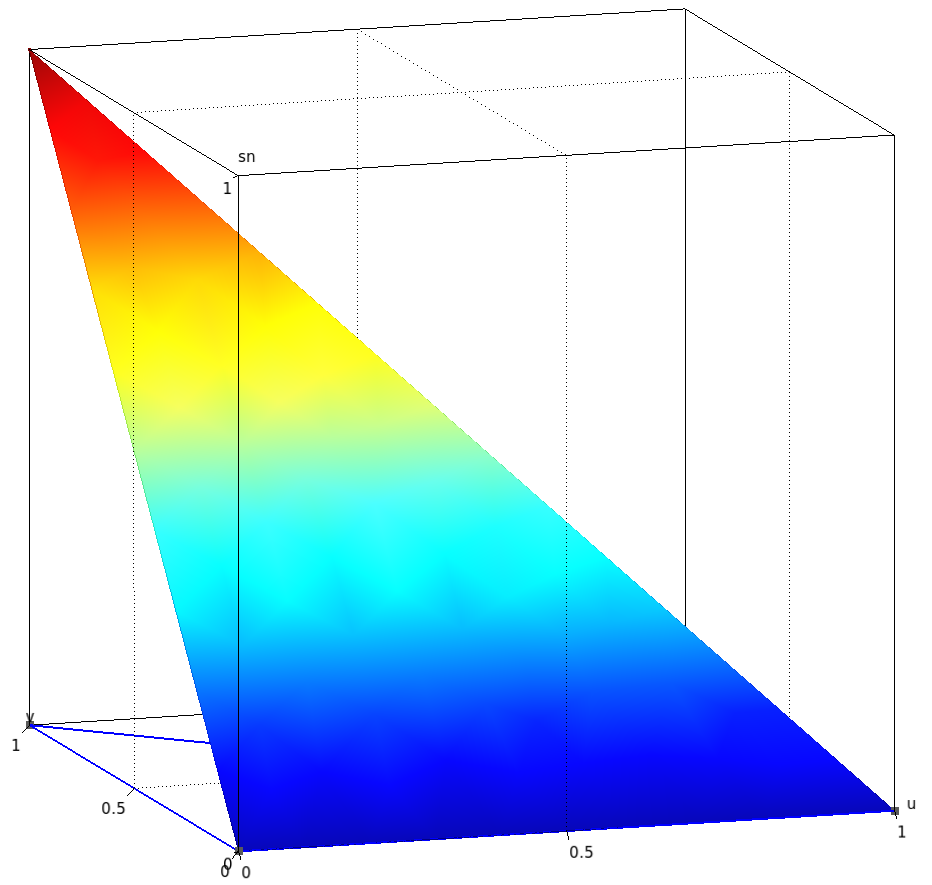
 |
Cas du quadrangle
Dans le cas du triangle de référence, ces fonctions sont données par la table ci-dessous :
| Nœud $i$ | Fonction de base $p_i (u,v)$ |
|---|---|
| 1 | $\displaystyle p_1 (u,v) = \frac{(1-u)(1-v)}{4}$ |
| 2 | $\displaystyle p_2 (u,v) = \frac{(1+u)(1-v)}{4}$ |
| 3 | $\displaystyle p_3 (u,v) = \frac{(1+u)(1+v)}{4}$ |
| 4 | $\displaystyle p_4 (u,v) = \frac{(1-u)(1+v)}{4}$ |
Une représentation graphique est donnée par :

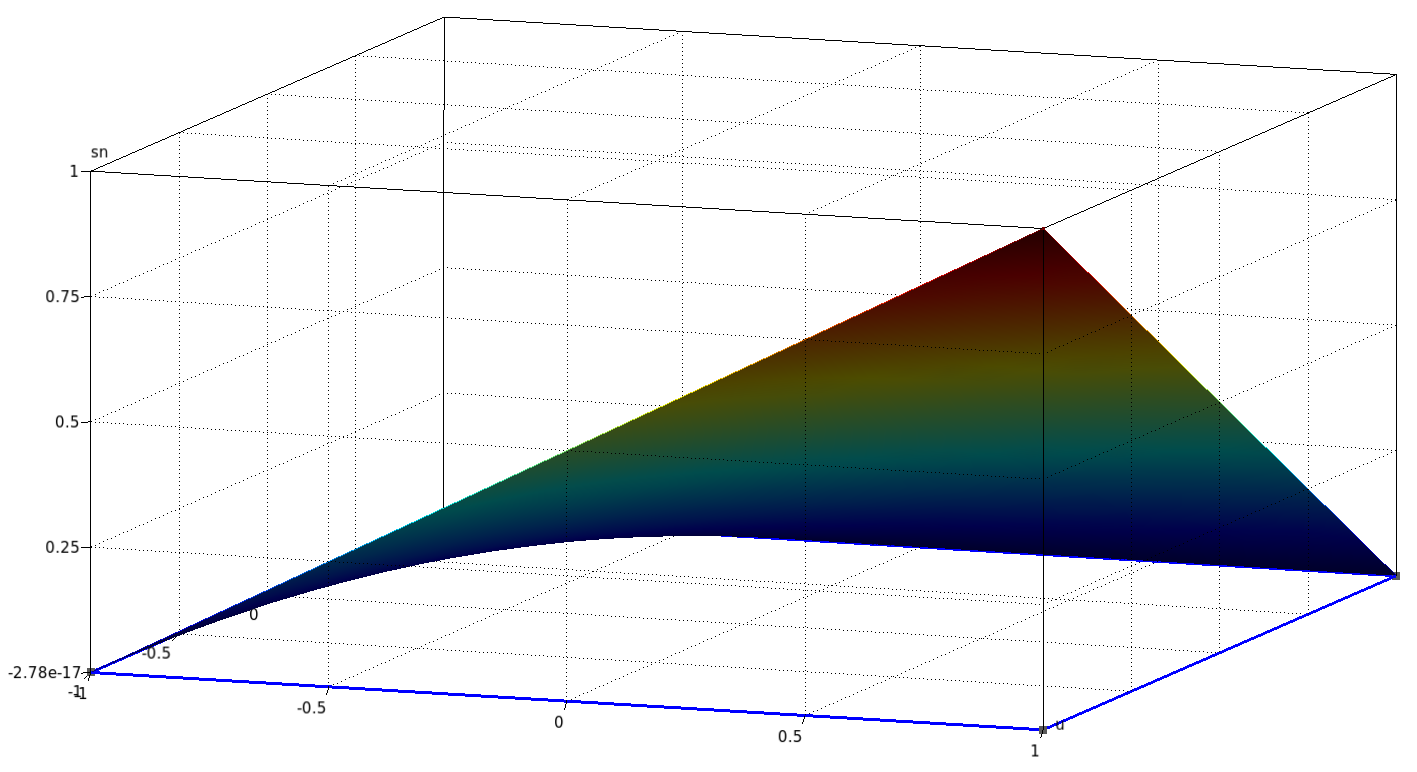
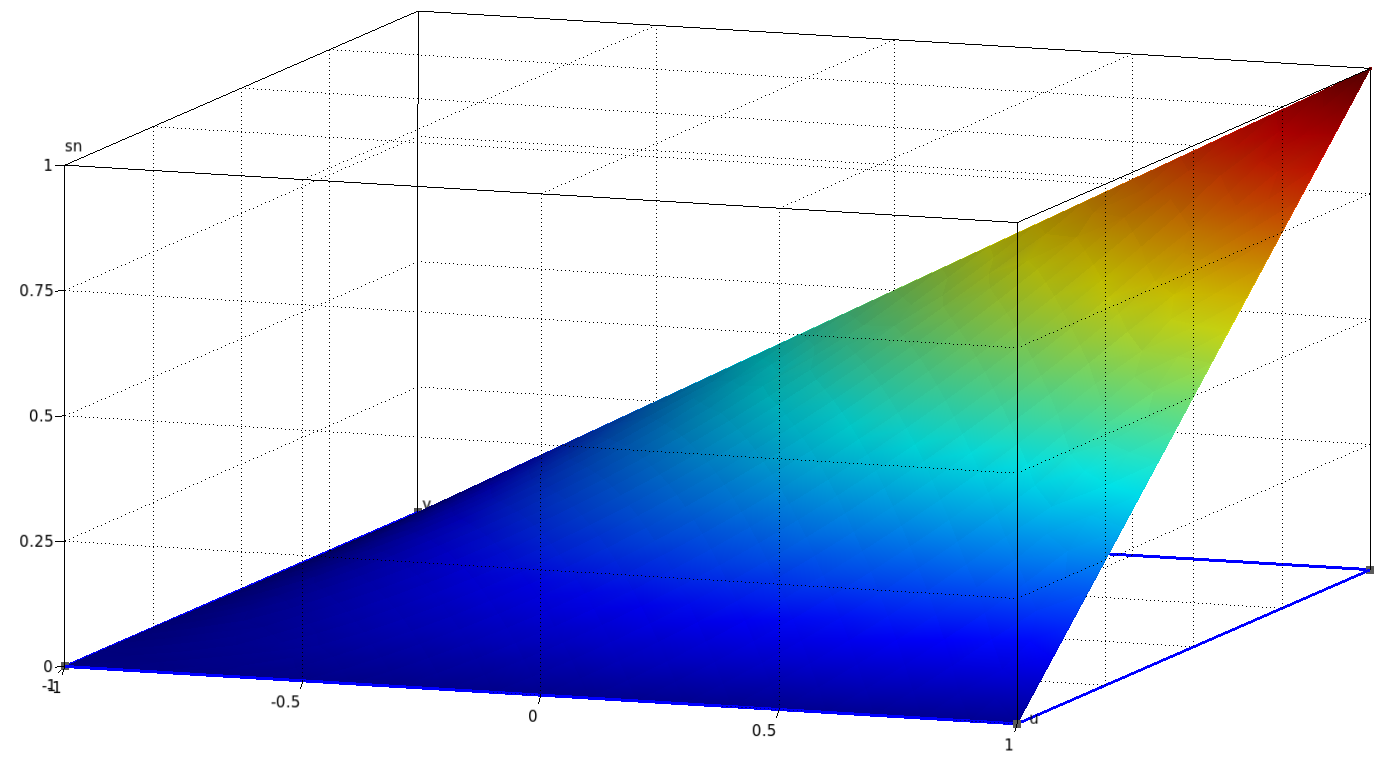
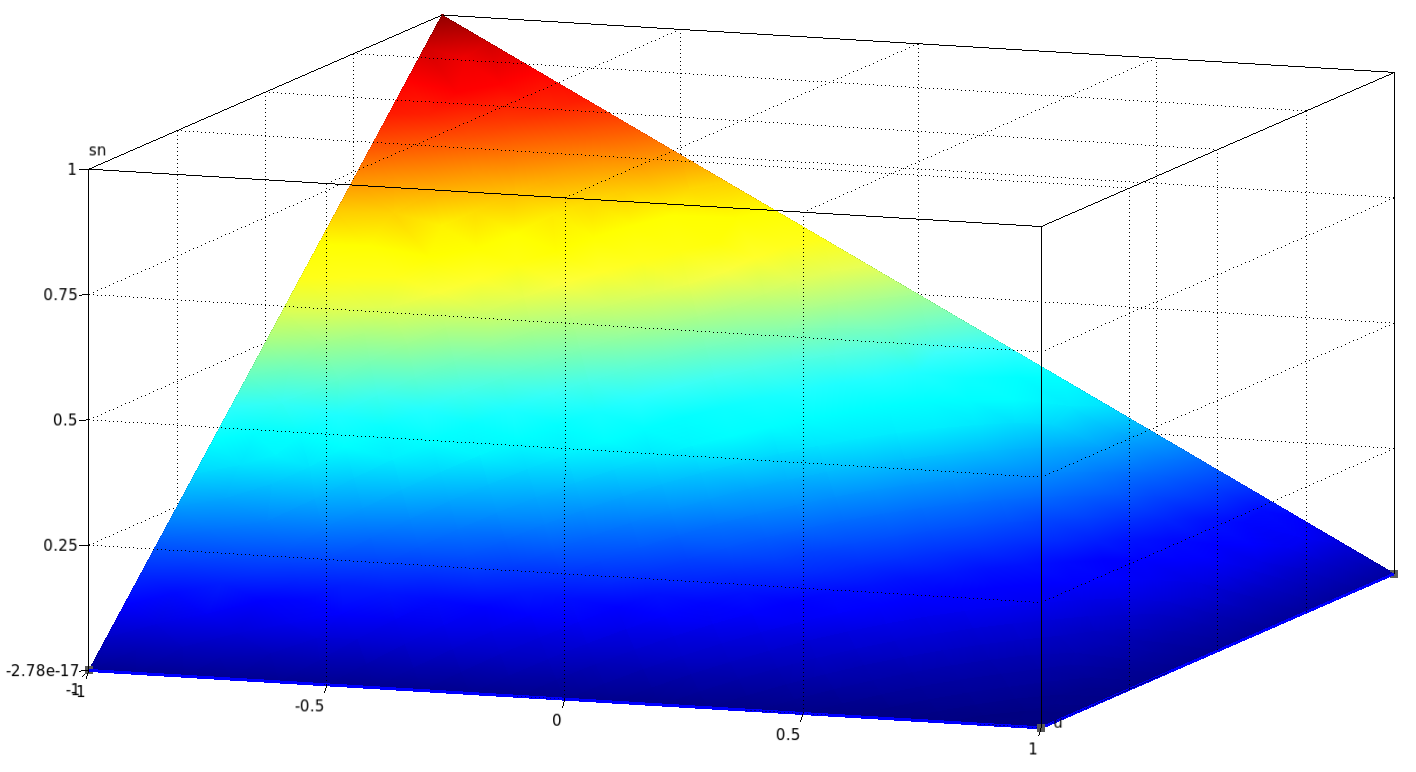
On peut également les tracer en surélevé :
| $p_1$ | $p_2$ | $p_3$ | $p_4$ |
|---|---|---|---|
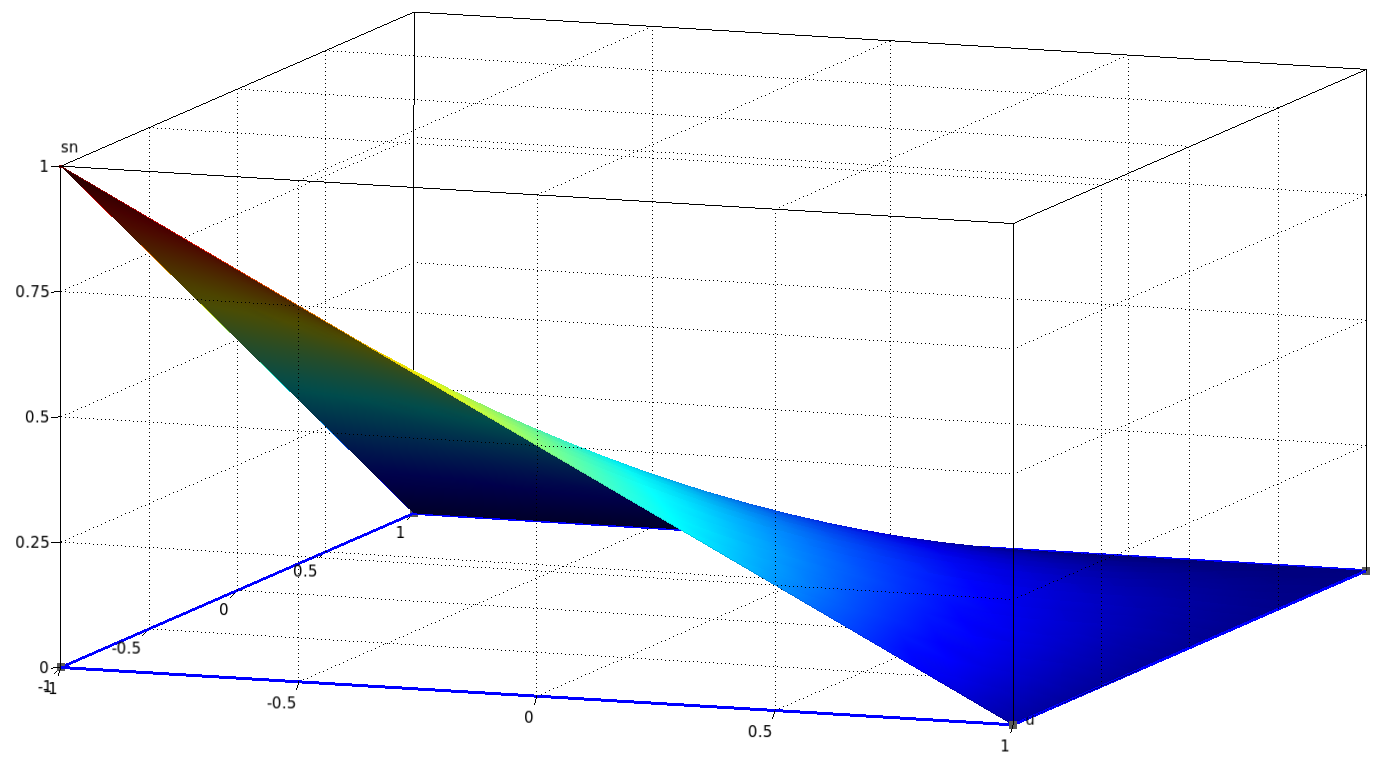
 |
 |
 |
 |
Cas du tétraèdre
Dans le cas du tétraèdre de référence, ces fonctions sont données par la table ci-dessous :
| Nœud $i$ | Fonction de base $p_i (u,v,w)$ |
|---|---|
| 1 | $p_1 (u,v,w) = 1 - u - v - w$ |
| 2 | $p_2 (u,v,w) = u$ |
| 3 | $p_3 (u,v,w) = v$ |
| 4 | $p_4 (u,v,w) = w$ |
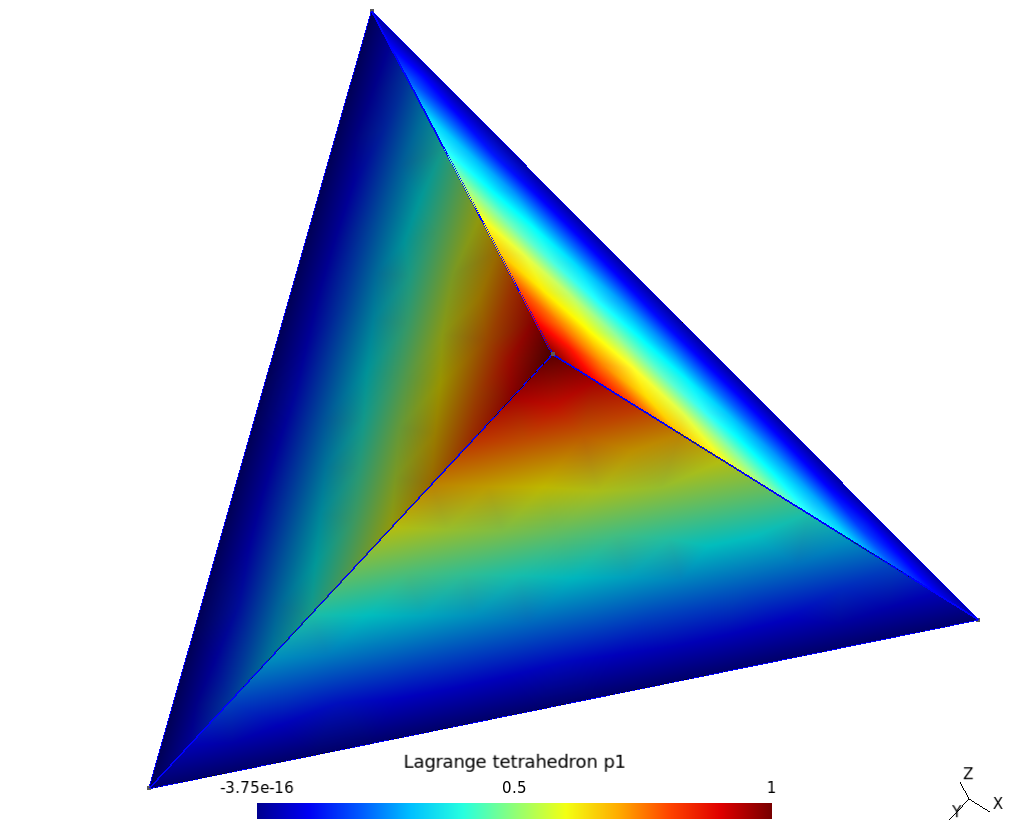
Et une représentation graphique de $p_1$ est donnée ci-dessous :
Cas de l’hexaèdre
Dans le cas de l’hexaèdre de référence, ces fonctions sont données par la table ci-dessous :
| Nœud $i$ | Fonction de base $p_i (u,v,w)$ |
|---|---|
| 1 | $\displaystyle p_1 (u,v,w) = \frac{(1-u)(1-v)(1-w)}{8}$ |
| 2 | $\displaystyle p_2 (u,v,w) = \frac{(1+u)(1-v)(1-w)}{8}$ |
| 3 | $\displaystyle p_3 (u,v,w) = \frac{(1+u)(1+v)(1-w)}{8}$ |
| 4 | $\displaystyle p_4 (u,v,w) = \frac{(1-u)(1+v)(1-w)}{8}$ |
| 5 | $\displaystyle p_5 (u,v,w) = \frac{(1-u)(1-v)(1+w)}{8}$ |
| 6 | $\displaystyle p_6 (u,v,w) = \frac{(1+u)(1-v)(1+w)}{8}$ |
| 7 | $\displaystyle p_7 (u,v,w) = \frac{(1+u)(1+v)(1+w)}{8}$ |
| 8 | $\displaystyle p_8 (u,v,w) = \frac{(1-u)(1+v)(1+w)}{8}$ |
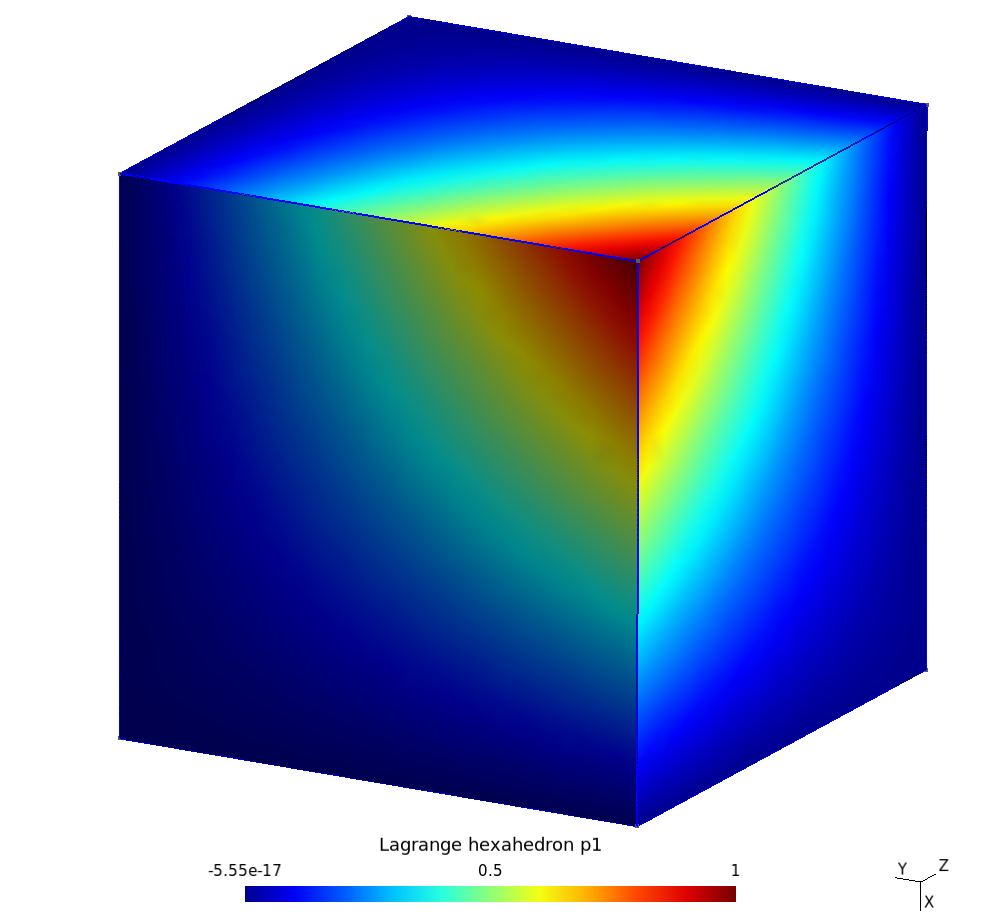
Et une représentation graphique de $p_1$ est donnée ci-dessous :
Éléments quelconques
Considérons maintenant un élément réel $K$ de $\mathcal{M}_h$, et intéressons nous à la transformation permettant de passer de l’élément de référence associé $K_r$ à cet élément, ainsi que sa réciproque.
Transformations géométriques
Soit ${\bf x}$ un point quelconque de $K$ de coordonnées $(x,y,z)$. Une paramétrisation possible de ${\bf x}$ est :
$${\bf x} = \begin{pmatrix}x\\y\\z\end{pmatrix} = \begin{pmatrix}x(u,v,w)\\y(u,v,w)\\z(u,v,w)\end{pmatrix} ={\bf x}({\bf u}) $$où ${\bf u} = (u,v,w) \in K_r$ permet de faire correspondre tout point $(x,y,z)$ de $K$ avec un point $(u,v,w)$ de $K_r$ de façon biunivoque (bijective). La transformation inverse est alors notée :
$${\bf u} = {\bf u}({\bf x})$$Une représentation schématique est donnée ci-dessous :
Les formules de différentiation des fonctions composées nous donnent alors :
$$\begin{pmatrix}\partial_u\\\partial_v\\\partial_w\end{pmatrix} = \underbrace{\begin{pmatrix}\partial_u\,x & \partial_u\,y & \partial_u\,z\\ \partial_v\,x & \partial_v\,y & \partial_v\,z\\ \partial_w\,x & \partial_w\,y & \partial_w\,z\end{pmatrix}}_{\displaystyle{\bf J}} \, \begin{pmatrix}\partial_x\\\partial_y\\\partial_z\end{pmatrix} $$$$\begin{pmatrix}\partial_x\\\partial_y\\\partial_z\end{pmatrix} = \underbrace{\begin{pmatrix}\partial_x\,u & \partial_x\,v & \partial_x\,w\\ \partial_y\,u & \partial_y\,v & \partial_y\,w\\ \partial_z\,u & \partial_z\,v & \partial_z\,w\end{pmatrix}}_{\displaystyle{\bf J^{-1}}} \, \begin{pmatrix}\partial_u\\\partial_v\\\partial_w\end{pmatrix} $$La matrice ${\bf J}$ est appelée matrice jacobienne de transformation. Les relations ci-dessus peuvent s’écrire sous forme plus compacte :
$$\partial_{\bf u} = {\bf J}\cdot\partial_{\bf x},~ ~ \text{avec :}~ ~ {\bf J} = \partial_{\bf u}\,{\bf x}$$$$\partial_{\bf x} = {\bf J^{-1}}\cdot\partial_{\bf u},~ ~ \text{avec :}~ ~ {\bf J^{-1}} = \partial_{\bf x}\,{\bf u}$$On rappelle au passage la formule de l’inverse :
$${\bf J^{-1}} = \frac{1}{\det {\bf J}}\,{}^{\operatorname {t} }\text{com}\,{\bf J}$$En pratique, on ne la calcule pas de cette façon. En effet, il est intéressant de remarquer que les colonnes de ${\bf J^{-1}}$ sont les gradients selon les coordonnées réelles ${\bf x}$ des fonctions $u({\bf x}),$ $v({\bf x}),$ et $w({\bf x})$. On les note : ${\bf grad_x}\,u({\bf x}),$ ${\bf grad_x}\,v({\bf x})$ et ${\bf grad_x}\,w({\bf x})$.
Nous pouvons calculer ces termes à partir des lignes de la matrice Jacobienne ${\bf J}$ qui sont ${}^{\operatorname t}\partial_u\,{\bf x},$ ${}^{\operatorname t}\partial_v\,{\bf x}$ et ${}^{\operatorname t}\partial_w\,{\bf x},$ et qui sont plus faciles à calculer.
Rappelons les deux propriétés de la comatrice suivantes :
$$\text{com}\,{}^{\operatorname t}{\bf M} = {}^{\operatorname t}\text{com}\,{\bf M}$$$${\bf M}\,{\bf a}\wedge{\bf M}\,{\bf b} = \text{com}\,{\bf M} \, ({\bf a}\wedge{\bf b})$$Ainsi, on a :
$$\begin{aligned}{\bf grad_x}\,u({\bf x}) &= {\bf J^{-1}}\,{\bf e_x} \\ &= \frac{1}{\det\,{\bf J}}\,{}^{\operatorname t}\text{com}\,{\bf J}\,{\bf e_x} \\ &= \frac{1}{\det\,{\bf J}}\,\text{com}\,{}^{\operatorname t}{\bf J}\,{\bf e_x}\\ &= \frac{1}{\det\,{\bf J}}\,\text{com}\,{}^{\operatorname t}{\bf J}\,({\bf e_y}\wedge{\bf e_z})\\ &= \frac{1}{\det\,{\bf J}}\, {}^{\operatorname t}{\bf J}\,{\bf e_y}\wedge{}^{\operatorname t}{\bf J}\,{\bf e_z}\\ &= \frac{1}{\det\,{\bf J}}\,\left(\partial_v\,{\bf x}\wedge\partial_w\,{\bf x} \right)\end{aligned}$$On peut faire de même pour les deux autres colonnes, au final, on obtient :
$$\boxed{\left\{\begin{aligned}{\bf grad_x}\,u({\bf x}) = \frac{1}{\det\,{\bf J}}\,\left(\partial_v\,{\bf x}\wedge\partial_w\,{\bf x} \right)\\[2ex] {\bf grad_x}\,v({\bf x}) = \frac{1}{\det\,{\bf J}}\,\left(\partial_w\,{\bf x}\wedge\partial_u\,{\bf x} \right) \\[2ex] {\bf grad_x}\,w({\bf x}) = \frac{1}{\det\,{\bf J}}\,\left(\partial_u\,{\bf x}\wedge\partial_v\,{\bf x} \right)\end{aligned}\right.}$$Le déterminant de la matrice jacobienne de transformation ($\det\,{\bf J},$ appelé Jacobien) peut se calculer par :
$$\det\,{\bf J} = \det\,{}^{\operatorname t}{\bf J} = \partial_u\,{\bf x}\cdot(\partial_v\,{\bf x}\wedge\partial_w\,{\bf x})$$Ce Jacobien est très important car il intervient directement dans les formules d’intégration sur l’élément $K$ qui sont (par la formule de changement de variable) :
$$\iiint_K f({\bf x})\,\text{d}{\bf x} = \iiint_{K_r} f\left({\bf x}({\bf u})\right)\,\det\,{\bf J}\,\text{d}{\bf u}$$Ci-dessous, vous trouverez une petite application permettant de calculer le Jacobien d’un triangle quelconque (avec l’aimable autorisation de son auteur B. Thierry) :
Déplacez les sommets du triangle pour modifier la valeur du Jacobien. Quand il est négatif cela signifie que le triangle est "retourné" par rapport au triangle de référence
Éléments isoparamétriques
Un élément isoparamétrique est un élément fini dont les fonctions de base nodales (qui permettent l’interpolation des champs scalaires) sont aussi utilisées pour paramétrer l’élément géométrique associé (fonctions d’interpolation géométrique) [Dula94].
Les fonctions de base vues ci-dessus sont définies par morceaux, sur chacun des éléments géométriques qui remplissent le domaine étudié, et permettent alors d’assurer leur continuité aux interfaces entre éléments. Ainsi, il n’y aura pas de discontinuité ni des champs scalaires interpolés, ni des coordonnées après transformation des éléments de référence vers les éléments réels. De telles fonctions de base sont dites conformes.
Considérons un élément fini nodal $(K,P_K,\Sigma_K)$. Si $n_K$ est l’ensemble des nœuds de $K$, de coordonnées ${\bf x_i},~i \in \mathbb{N},$ et si les $p_i({\bf u}),~i \in [\![1,n_K]\!],$ sont ses fonctions de base exprimées dans les coordonnées ${\bf u}$ de l’élément de référence $K_r$ associé à $K$, alors la paramétrisation de $K$ $\left({\bf x} = {\bf x}({\bf u})\right)$ est donnée par :
$$\boxed{{\bf x} = \sum\limits_{i = 1}^{n_K} {\bf x_i}\,p_i({\bf u})}$$et cet élément est isoparamétrique.
Remarque
Dans ce cas, les fonctions de base permettent de passer de l’élément de référence à un élément réel et ainsi de déterminer la forme de ce dernier. C’est pour cela qu’on les appelle aussi fonctions de forme.
Fonctions de base globales
À l’aide de la transformation géométrique précédente et des fonctions de bases $p_i,~i \in [\![1, n_K]\!]$ définies sur l’élément de référence, nous pouvons définir les fonctions de base globales $\varphi_i,~i \in [\![1, n_h]\!]$ définies sur le maillage complet $\mathcal{M}_h$. Il y en aura autant que de nœuds et chacune sera liée à un nœud particulier. Elle seront non-nulles uniquement sur les éléments contenant le nœud considéré. Cet ensemble d’éléments est appelé le support de la fonction de base.
Finalement, d’après ce qui précède, la fonction de base $\varphi_k$ liée au nœud $k \in [\![1, n_h]\!]$ sera nulle sur tous les nœuds du maillage sauf le nœud $k$ où elle prendra la valeur $1$. Soit, en notant ${\bf x_j}$ les coordonnées du nœud $j$ :
$$\boxed{\forall i,j \in [\![1,n_h]\!], ~ \varphi_i({\bf x_j}) = \delta_{ij}}$$Une illustration interactive est donnée par l’application suivante (toujours avec l’aimable autorisation de son auteur) :
Application : Cliquez sur un sommet pour faire apparaitre la fonction de forme $\mathbf{P_1}$ associée. Les triangles où la fonction n’est pas nulle forment le support de la fonction de forme.
La famille $(\varphi_i)_{0\le i \le n_h}$ ainsi construite forme une base de $V_h$ qui est donc de dimension $n_h$ égale aux nombre de nœuds du maillage $\mathcal{M}_h$.
Soit $u_h$ une fonction de $V_h$. En la décomposant dans la base obtenue :
$$ u_h = \sum\limits_{i = 1}^{n_h} u_i\,\varphi_i$$Les coefficients $u_i$ sont en fait les valeurs de la fonctions au nœuds. En effet en appliquant en ${\bf x_j}$ :
$$u_h({\bf x_j}) = \sum\limits_{i = 1}^{n_h} u_i\,\varphi_i({\bf x_j}) = u_j$$Finalement, une fonction $u_h$ de $V_h$ se décompose donc dans la base $(\varphi_i)_{0\le i \le n_h}$ selon :
$$\boxed{u_h = \sum\limits_{i = 1}^{n_h} u_h({\bf x_i})\,\varphi_i}$$et elle est entièrement caractérisée par ses $n_h$ valeurs aux nœuds.
Remarques complémentaires importantes
-
Dans le cas présenté, les fonctions de base de l’élément de référence servent aussi à paramétrer les éléments réels (fonctions d’interpolation géométrique). Cela correspond au cas particulier des éléments isoparamétriques, mais ces deux types de fonctions sont indépendants l’un de l’autre :
- On pourrait tout à fait utiliser des fonctions de base d’ordre 2 (interpolation quadratique) ou d’ordre 3 (interpolation cubique) avec la transformation géométrique précédente (et les éléments rectilignes précédents). Un exemple fonctionnant sous Onelab vous sera fourni page suivante.
- On pourrait utiliser des fonctions d’interpolation géométrique d’ordre 2 pour définir des éléments courbes. Le cas isoparamétrique (ou les deux types de fonctions sont d’ordre 2) correspond aux éléments dits $\mathbf{P_2}$ (ou $\mathbf{Q_2}$ si quadrangles).
-
Les éléments présentés ci-dessus conviennent parfaitement pour représenter des champs scalaires, nous verrons plus tard lesquels utiliser pour les champs vectoriels.
-
Plus que les fonctions de bases globales, ce sont les fonctions de base sur les éléments de référence et la matrice Jacobienne qui sont utiles pour créer le système à résoudre, c’est ce que nous allons voir de suite.