Décomposition sous forme de Jordan
Dans le cas où la matrice étudiée n'est ni diagonalisable, ni nilpotente, et si la décomposition précédente (somme d'une matrice diagonalisable et d'un nilpotente) n'apparaît pas de façon évidente : on utilise ce que l'on appelle la « réduction de Jordan ».
Rappel : Théorème spectral
Soit \({\bf A}\) la matrice associée à un endomorphisme \(A\) de \(E\). Le théorème spectral permet de décomposer \(E\) comme la somme directe des sous espaces spectraux (cf cours d'algèbre), soit :
\(E = \bigoplus_{i=1}^{p} E_i\), où \(E_i = Ker\,( A - \lambda_i~ Id)^{r_i}\), avec \(r_i \leq\) à la multiplicité de \(\lambda_i\) (valeur propre de \({\bf A}\)).
On a les propriétés suivantes :
L'image de chacun des \(E_i\) par \(A\) est stable \(\big(A(E_i) \subset E_i\big)\).
Par définition des \(E_i\), il existe \(r_i\) tel que :
\(\Phi_i^{(r_i)} = 0\), où \(\Phi_i = A|_{E_i} - \lambda_i~Id_{E_i}~:~E_i\rightarrow E_i\).
Ainsi \(Ker~\Phi_i^{(k)}, k=0,1,2,\dots\) forment une suite strictement croissante et on a :
\(\{0\} = Ker~\Phi_i^{(0)} \subset Ker~\Phi_i^{(1)} \subset \cdots \subset Ker~\Phi_i^{(r_i)} = E_i\)
Méthode : Mise sous forme de Jordan
On construit une base des \(E_i\) de la manière suivante :
On cherche tous les \(v_i\) tels que \(v_i \in Ker~\Phi_i\).
Puis pour chacun des vecteurs \(v_i\) trouvés, on cherche les \(w_i\) tels que \(v_i = \Phi_i(w_i)\).
On voit alors que : \(w_i \in Ker~\Phi_i^{2}\) et \(w \notin Ker~\Phi_i\).
On itère le procédé jusqu'à épuisement = jusqu'à trouver autant de vecteurs de base que la dimension \(n\) du problème, quitte à aller les chercher jusque dans \(Ker~\Phi_i^{r_i}\).
Au final dans la base de \(E_i\) ainsi construite, \({\bf A|_{E_i}}\) la matrice associée à \({A|_{E_i}}\) (restriction de l'application \(A\) à l'espace \(E_i\)) prend la forme d'une matrice de Jordan (ou bloc de Jordan) :
\({\bf A|_{E_i}} = {\bf P_i} \cdot \underbrace{ \begin{pmatrix} \lambda_i & 1 & 0 & \cdots & 0 \\ 0 & \lambda_i & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ \vdots & & \ddots & \lambda_i & 1 \\ 0 & \cdots & \cdots & 0 & \lambda_i \end{pmatrix} }_{{\bf J_{\lambda_i}}~(\text{de dim}~r_i\times r_i)} \cdot {\bf P_i}^{-1}\)
Avec \({\bf P_i}\), matrice de passage à la base de \(E_i\) ainsi créée.
\(~\)
Ainsi dans la base finale constituée des vecteurs des différentes bases des \(E_i\) construites par la méthode précédente, notre matrice initiale s'écrit sous la forme de Jordan :
\({\bf A} = \begin{pmatrix} {\bf A|_{E_1}} & & 0 \\ & \ddots & \\ 0 & & {\bf A|_{E_p}} \end{pmatrix} = {\bf P} \cdot \begin{pmatrix} {\bf J_{\lambda_1}} & & 0 \\ & \ddots & \\ 0 & & {\bf J_{\lambda_p}} \end{pmatrix} \cdot {\bf P}^{-1}\), avec \({\bf P} = \begin{pmatrix} {\bf P_1} & \cdots & {\bf P_p} \end{pmatrix}\)
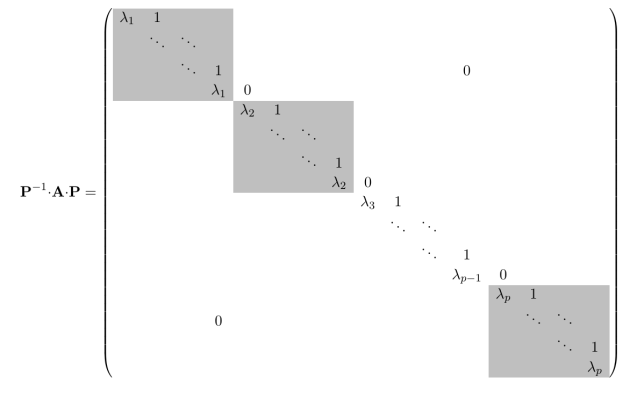
Forme de Jordan (représentation générale)
Finalement la forme complète est donnée par la figure ci-dessous (cliquer sur le titre sous la figure pour plus de détails) :
Forme de Jordan d'une matrice quelconque : chaque bloc de Jordan apparaît en grisé, tous les autres termes que ceux écrits sont nuls.
On obtient ainsi la forme la plus simple possible : les valeurs propres sur la diagonale et uniquement des uns et des zéros sur la diagonale supérieure.
Les blocs peuvent être de dimension 1 (c'est-à-dire des scalaires) ; pour une matrice diagonalisable, ils le sont même tous.
\(~\)
Exemple : Réduction de Jordan
Cherchons la forme de Jordan de la matrice :
\({\bf A} = \begin{pmatrix} 4 & 2 & 0\\ 1 & 5 & -1\\ -1 & 1 & 5 \end{pmatrix}\)
Le polynôme caractéristique de \({\bf A}\) est (après calculs) : \(P_A(\lambda) = (\lambda -4)^2(\lambda-6).\)
On résout : \(({\bf A} - 6~{\bf I_3})\cdot x = 0,\) et on trouve :
\(v_6 = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}.\)
Le sous espace spectral \(E_1 = Ker (A - 6 Id)\) est donc engendré par \(v_6\).
On résout ensuite : \(({\bf A} - 4~{\bf I_3})\cdot x = 0,\) on trouve un seul vecteur :
\(v_4 = \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}.\)
On en déduit donc que \(E_2 = Ker (A - 4 Id)^2\).
On cherche alors \(w_4\) tel que \(v_4 = ({\bf A} - 4~{\bf I_3})\cdot w_4\), et on trouve :
\(w_4 = \begin{pmatrix} -\frac{1}{2} \\ \frac{1}{2} \\ 0 \end{pmatrix}.\)
Ainsi \(\mathbb{R}^3 = E_1 \oplus E_2\) et dans la base \(\{v_6,v_4,w_4\}\), \({\bf A}\) s'écrit :
\({\bf P}^{-1}\cdot{\bf A}\cdot{\bf P} = \begin{pmatrix} 6 & 0 & 0\\ 0 & 4 & 1\\ 0 & 0 & 4 \end{pmatrix},\) avec \({\bf P}= \begin{pmatrix} v_6 & v_4 & w_4 \end{pmatrix} = \begin{pmatrix} 1 & 1 & -\frac{1}{2}\\ 1 & 0 & \frac{1}{2}\\ 0 & 1 & 0 \end{pmatrix}\)
Intérêt de la décomposition :
Une fois le processus fini, on obtient directement la décomposition de la partie précédente.
En effet, on a :
\({\bf A} = {\bf P}\cdot \begin{pmatrix} \delta_1 & * & 0 & \cdots & 0 \\ 0 & \delta_2 & * & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & 0 \\ \vdots & & \ddots & \ddots & * \\ 0 & \cdots & \cdots & 0 & \delta_n \\ \end{pmatrix} \cdot{\bf P}^{-1},\)
où les \(\delta_j\) sont des valeurs propres de \({\bf A}\) et les \(* = 0~\text{ou}~1\).
Ainsi :
\({\bf A} = {\bf P}\cdot \underbrace{ \begin{pmatrix} \delta_1 & & & 0\\ & \delta_2 \\ & & \ddots \\ 0& & & \delta_n \\ \end{pmatrix}}_{{\bf \Delta}~\text{(diagonale)}} \cdot{\bf P}^{-1} + {\bf P}\cdot \underbrace{ \begin{pmatrix} 0 & * & & 0 \\ & 0 & \ddots \\ & & \ddots & * \\ 0 & & & 0 \\ \end{pmatrix}}_{{\bf N}~\text{(nilpotente)}} \cdot{\bf P}^{-1}\)
On en déduit :
\(\left\{ \begin{array}{l} \exp({\bf A})= \left[{\bf P}\cdot \exp({\bf \Delta}) \cdot{\bf P}^{-1} \right]\cdot\left[ {\bf P}\cdot \exp({\bf N}) \cdot{\bf P}^{-1}\right]= {\bf P}\cdot\exp({\bf \Delta})\cdot\exp({\bf N})\cdot{\bf P}^{-1}\\ ~\\ \text{Avec :}~~\exp({\bf N}) = {\bf I_n} + {\bf N} + \dfrac{{\bf N}^2}{2} + \cdots + \dfrac{{\bf N}^{(q-1)}}{(q-1) !}, ~~~~(q \leq n) \end{array} \right.\)
\(~\)
Exemple : (suite de l'exemple précédent)
Déduisons des calculs précédents l'exponentielle de notre matrice :
\({\bf P}^{-1}\cdot{\bf A}\cdot{\bf P} = \begin{pmatrix} 6 & 0 & 0\\ 0 & 4 & 1\\ 0 & 0 & 4 \end{pmatrix} = \underbrace{ \begin{pmatrix} 6 & 0 & 0\\ 0 & 4 & 0\\ 0 & 0 & 4 \end{pmatrix}}_{{\bf \Delta}} + \underbrace{ \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{pmatrix}}_{\bf N}\)
\(\left\{ \begin{array}{l} \exp({\bf \Delta}) = \begin{pmatrix} e^6 & 0 & 0\\ 0 & e^4 & 0\\ 0 & 0 & e^4 \end{pmatrix}\\ {\bf N}^2 = {\bf 0_3} ~~\Rightarrow~~ \exp({\bf N}) = {\bf I_3} + {\bf N} = \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 1\\ 0 & 0 & 1 \end{pmatrix} \end{array}\right.\)
On calcule l'inverse de la matrice de passage :
\({\bf P}= \begin{pmatrix} 1 & 1 & -\frac{1}{2}\\ 1 & 0 & \frac{1}{2}\\ 0 & 1 & 0 \end{pmatrix} ~~\Rightarrow~~ {\bf P}^{-1}= \begin{pmatrix} \frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\\ 0 & 0 & 1\\ -1 & 1 & 1 \end{pmatrix}\)
On a ainsi :
\({\bf P}^{-1}\cdot\exp({\bf A})\cdot{\bf P} = \exp({\bf \Delta})\cdot\exp({\bf N}) = \begin{pmatrix} e^6 & 0 & 0\\ 0 & e^4 & e^4\\ 0 & 0 & e^4 \end{pmatrix}\)
Soit :
\(\exp({\bf A}) ={\bf P}\cdot \begin{pmatrix} e^6 & 0 & 0\\ 0 & e^4 & e^4\\ 0 & 0 & e^4 \end{pmatrix}\cdot{\bf P}^{-1} = \frac{1}{4} \begin{pmatrix} 2(e^6+e^4) & 2e^6 & e^4-e^6\\ 0 & 4 e^4 & 0\\ 4 (e^4 - e^6) & 4 (2 e^4 - e^6) & 2(e^6+e^4) \end{pmatrix}\)